Sistema de Funciones Iteradas:Fractales Autosemejantes |
Contenido de esta página:
-
Definiciones y teoremas previos
-
Construcción de fractales autosemejantes:
Definición 1
Decimos que la aplicación
$$ f: \mathbb{R^n} \rightarrow \mathbb{R^n} $$
es una semejanza si existe un real positivo k tal que para cualquier par de puntos
$$ x,y \in \mathbb{R^n} $$
se cumple que la distancia entre las imágenes de dichos puntos es
$$ d(f(x),f(y)) = k\cdot d(x,y) $$
El número k se denomina razón o factor de semejanza de f y si es menor que 1, k < 1, entonces se dice que la semejanza f es contractiva.
Definición 2 (teorema)
Sea (X,d) un espacio métrico y sea la contracción
$$ f:(X,d) \rightarrow (X,d) $$
Entonces, existe un único punto x de X, al que llamamos atractor de f, que cumple
$$f(x) = x $$
Nota: la existencia del atractor se justifica con el Teorema del Punto Fijo de Banach.
Definición 3 (teorema)
El espacio métrico
$$(K( \mathbb{R^n}), d_H)$$
es completo, siendo
$$ K ( \mathbb{R^n}) := \{ K \subseteq \mathbb{R^n}\ |\ K \neq \emptyset, \ K\ compacto \} $$
Y dh la distancia de Hausdorff.
Nota: omitimos la demostración de que el espacio anterior es métrico y de que, además, es completo (Teorema de Selección de Blaschke).
El gran resultado que nos permitirá definir los fractales autosemejantes es el siguiente:
Teorema 1
Sea el sistema de semejanzas contractivas
$$\{ f_1, …, f_m \}$$
siendo las aplicaciones
$$ f_i: \mathbb{R^n} \rightarrow \mathbb{R^n} $$
con razones de semejanza
$$ 0< r_i < 1 $$
Entonces, existe un único compacto
$$ K \in K(\mathbb{R^n}) $$
que cumple
$$ K = f_1(K) \cup f_2(K) \cup...\cup f_m(K) $$
Observaciones:
De la propia demostración del Teorema del Punto Fijo de Banach se desprende que para cualquier punto x del espacio X, la sucesión xi construida por la composición de la contracción H consigo misma,
$$ x_i = H^i(x),\ i\in \mathbb{N} $$
converge al atractor de H.
Definición 4
Sea el conjunto de aplicaciones contractivas
$$ \{ f_1,…,f_m \}$$
siendo
$$ f_i: \mathbb{R^n} \rightarrow \mathbb{R^n} $$
con factores de contractividad 0 < ri < 1.
Entonces decimos que es un sistema de funciones iteradas (SFI) con razón de contractividad
$$ r = sup \{ r_i\ |\ i=1,...,m \} $$
Con las definiciones y teoremas anteriores ya podemos definir los fractaes autosemejantes:
Fractal Autosemejante
Dado el SFI de la definición 4, llamamos fractal autosemejante al atractor K (K es compacto) del SFI.
Observaciones:
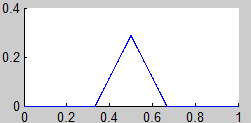
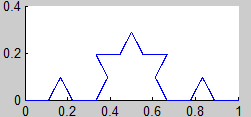
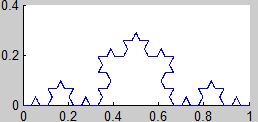
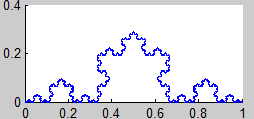
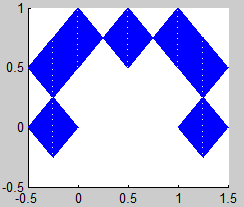
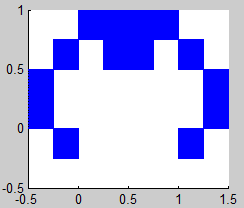
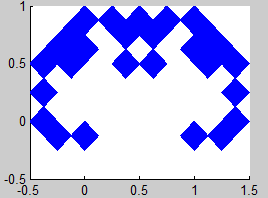
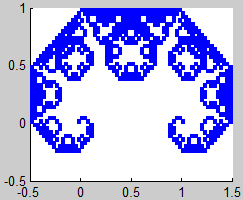
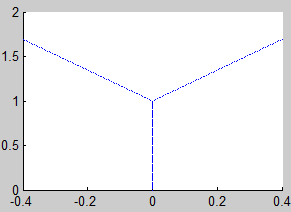
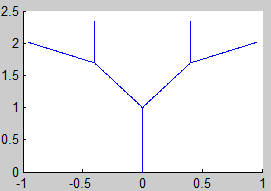
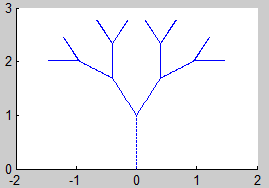
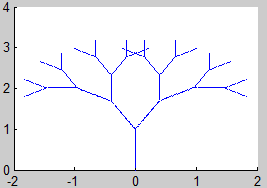
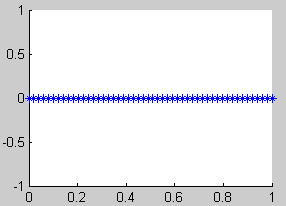
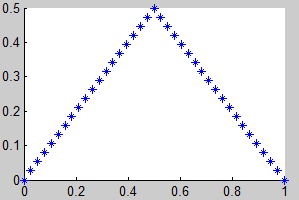
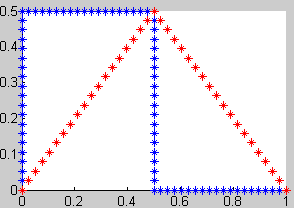
Según las observaciones del teorema 1, el atractor K (el fractal) lo podemos obtener como el límite de la sucesión
$$ K_i = H^i (K_0),\ i=1,2,3… $$
siendo K0 un compacto cualquiera del espacio y H la aplicación contractiva definida en el teorema 1:
$$ H(K_0) = f_1 (K_0) \cup ...\cup f_m(K_0) $$
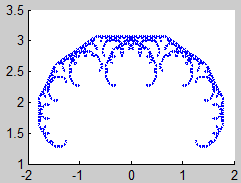
El resto de la página lo dedicamos a ver ejemplos de fractales autosemejantes.
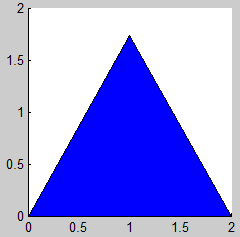
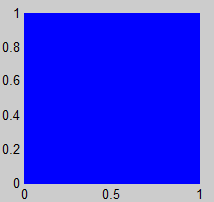
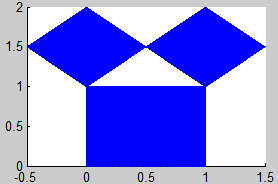
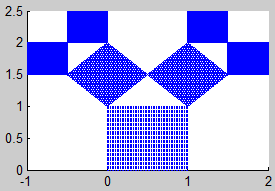
En cada uno de los fractales buscaremos el sistema de iteradas contractivas que lo definen. Consideramos un compacto inicial y calcularemos la sucesión de compactos que genera para obtener aproximaciones del atractor del sistema.
Empezamos con un fractal sencillo y famoso:
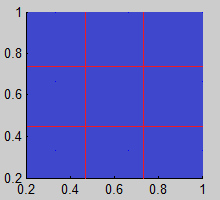
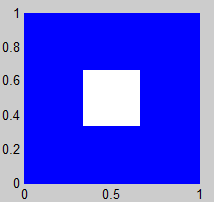
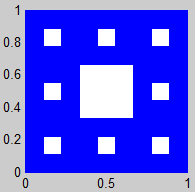
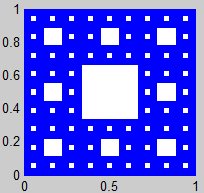
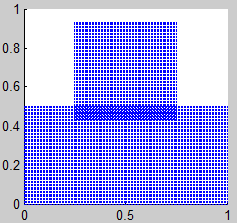
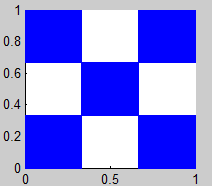
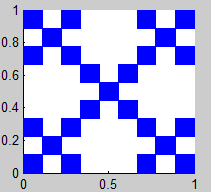
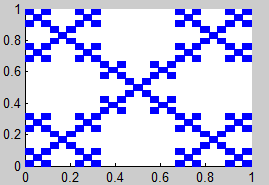
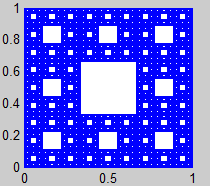
1. Alfombra de Sierpinski
(Sierpinski Carpet)
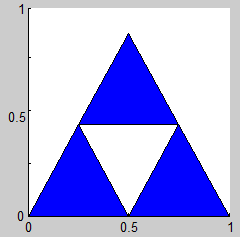
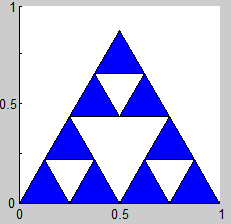
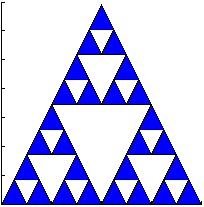
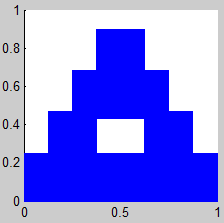
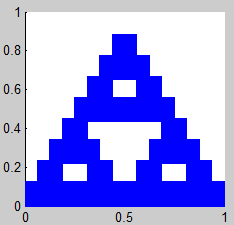
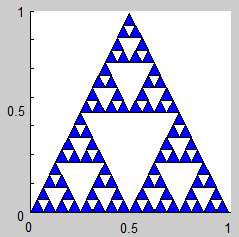
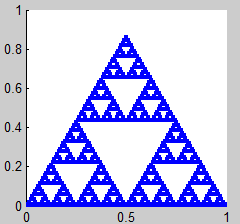
2. Triángulo de Sierpinski
(Sierpinski Triangle, Sierpinski Gasket, Sierpinski Sieve)
3. Triángulo de Sierpinski (2)
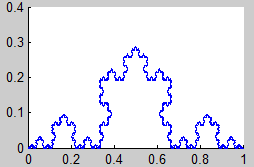
4. Curva de Koch
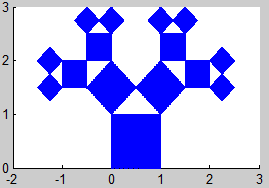
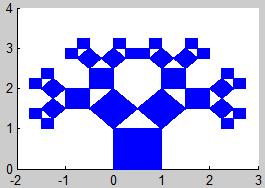
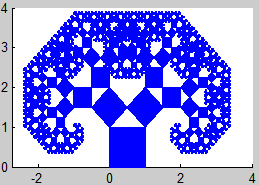
5. Árbol de Pitágoras
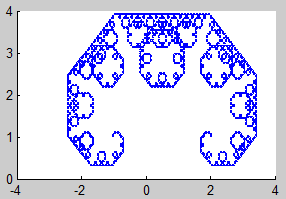
6. Dragón de Levy

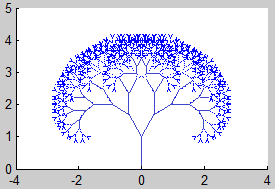
7. Árbol Binario
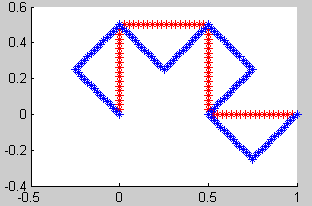
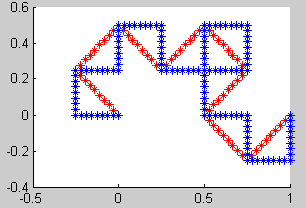
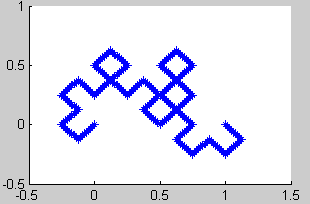
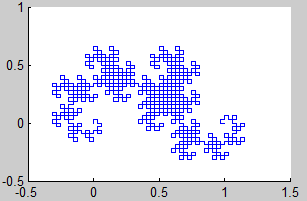
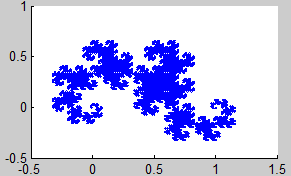
8. Dragón de Heighway
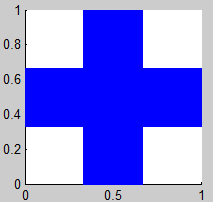
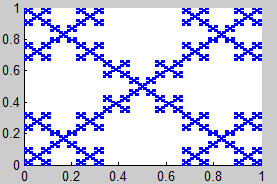
9. Fractal de Vicsek
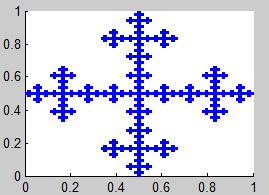
10. Fractal de Vicsek (2)

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.