Contenido de esta página:
Definición de función
Definición informal de inversa
Definiciones previas
Definición de función inversa
Cuestiones sobre la inversa
Obtención de la inversa
Problemas resueltos
Una función de variable real, \(f:A\rightarrow B\), es una relación entre dos conjuntos \(A\) y \(B\) de los números reales que a cada número \(x\) de \(A\) le hace corresponder un único número de \(B\), denotado por \(f(x)\) y llamado imagen de \(x\) mediante \(f\).
De ahora en adelante, supondremos \(f:A\rightarrow B\), siendo \(A\) y \(B\) subconjuntos de los números reales \(\mathbb{R}\). \(A\) es el dominio de \(f\) y \(B\) es su codominio.
Nota: \(B\) es el codominio y cumple \(f(A)\subseteq B\). El conjunto \(f(A)\) es la imagen de \(f\).
Informalmente, la función inversa de \(f\) es la función \(f^{-1}:B\rightarrow A\) tal que dado un número \(y\) de \(B\), permite conocer el número \(x\) de \(A\) tal que \(y=f(x)\). Se escribe \(f^{-1}(y) = x\).
Ejemplo:
Si \(f(x) = 2x\), su inversa es \(f^{-1}(x) = x/2\). Por ejemplo,
$$ f^{-1}(8) =8/2 = 4$$
En efecto, la imagen de 4 es 8:
$$ f(4) = 2\cdot 4 = 8$$
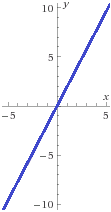
Ejemplo introductorio:
La función \(f(x) = x^2\) no tiene inversa ya que, por ejemplo, \(f^{-1}(4)\) podría ser \(f^{-1}(4)=2\) o bien \(f^{-1}(4)=-2\):
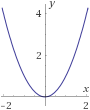
Nota: si restringimos el dominio de \(f\) a los reales no negativos o a los no positivos, la función sí tiene inversa.
Teniendo en cuenta la definición dada para una función \(f\), como \(f^{-1}\) también es una función, debe exigirse que cada número \(y\) de \(B\) tenga una única imagen \(x=f^{-1}(y)\) en \(A\). Al número \(x\) tal que \(f^{-1}(y) = x\) se le denomina anti-imagen de \(y\) mediante \(f\).
Matemáticamente, esta exigencia de la unicidad de la anti-imagen (para que sea una función) se traduce exigiendo que la función \(f\) sea inyectiva:
La función \(f:A\rightarrow B\) es inyectiva si cumple
$$ f(x) = f(y) \leftrightarrow x=y, \forall x,y\in A$$
Es decir, \(f\) es inyectiva si: la imagen de dos números de \(A\) son iguales si, y solamente si, dichos números de \(A\) son el mismo número.
Asimismo, como función, la inversa \(f^{-1}\) debe proporcionar la anti-imagen de todos los números de \(B\). Sin embargo, esto no es posible si algún número de \(B\) no es la imagen de algún número de \(A\).
Matemáticamente, este problema se soluciona exigiendo que la función \(f\) sea sobreyectiva (o suprayectiva):
La función \(f:A\rightarrow B\) es sobreyectiva (o suprayectiva) si cumple
$$ \forall y\in B, \ \exists x\in A,\ f(x) = y $$
Es decir, \(f\) es sobreyectiva si todo número de \(B\) es la imagen mediante \(f\) de algún número de \(A\).
Debido a la importancia de la inyectividad y sobreyectividad de una función simultáneamente, existe una definición que considera ambas propiedades:
La función \(f:A\rightarrow B\) es biyectiva si es inyectiva y sobreyectiva.
Veamos la definición formal de función inversa:
La función inversa \(f^{-1}\) de una función biyectiva \(f:A\rightarrow B\) es la la función \(f^{-1}:B\rightarrow A\) que cumple
$$ f^{-1}(f(x)) = x, \ \forall x\in A$$
$$ f(f^{-1}(y)) = y, \ \forall y\in B$$
Dicho en otras palabras,
$$ f^{-1}\circ f = id_A $$
$$ f\circ f^{-1} = id_B $$
donde \(id_A\) es la función identidad de \(A\):
$$ id_A:A\rightarrow A$$
$$id_A (x)=x,\ \forall x\in A$$
e \(id_B\) es la función identidad de \(B\):
$$ id_B:B\rightarrow B$$
$$id_B (y)=y,\ \forall y\in B$$
Cuestión 1
Si \(f^{-1}:B\rightarrow A\) cumple las condiciones dadas en la definición de función inversa de \(f\), ¿es realmente la inversa de \(f\)? Es decir, ¿\(f^{-1}\) proporciona las anti-imágenes de \(f\)?
Supongamos que \(x\) es un número de \(A\). Entonces, tiene una imagen mediante \(f\):
$$ \exists y=f(x)\in B $$
En efecto, \(f^{-1}\) proporciona la anti-imagen de \(y\) aplicando la primera condición:
$$ f^{-1}(y) = f^{-1}(f(x)) = x $$
Cuestión 2:
¿La función inversa es única?
La respuesta es sí. Veamos el razonamiento:
Supongamos que la función \(g:B\rightarrow A\) cumple las condiciones de la inversa de \(f\).
Sea \(y\) un número de \(B\). Como \(f\) es biyectiva, existe un número \(x\) de \(A\) tal que \(y = f(x)\).
Se tiene que
$$ g(y) = x$$
Pero también,
$$ f^{-1}(y) = x $$
Por tanto,
$$ g(y) = f^{-1}(y),\ \forall y\in B$$
Esto demuestra que la inversa es única puesto que la imagen de cualquier número \(y\) de \(B\) mediante \(g\) coincide con la imagen mediante \(f^{-1}\). Es decir, las funciones son iguales porque están definidas entre los mismos conjuntos y la imagen de cada número de \(B\) coincide.
La definición de la inversa no indica cómo calcular la inversa de una función dada. El método que suele utilizarse es:
Si la expresión de\(f:A\rightarrow B\) es función de \(x\), \(y=f(x)\), es suficiente con aislar \(x\). Después, se cambia la \(x\) por la \(y\) y viceversa para obtener \(y=f^{-1}(x)\).
Ejemplo:
Sea la función biyectiva
$$ f(x) = \frac{2x+1}{5} $$
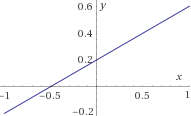
Para calcular \(f^{-1}\), aislamos \(x\):
$$ y = \frac{2x+1}{5} \rightarrow $$
$$ 5y = 2x+1 \rightarrow $$
$$ 5y-1 = 2x \rightarrow $$
$$ x = \frac{5y-1}{2} $$
Cambiamos \(x\) por \(y\):
$$ y = \frac{5x-1}{2} \rightarrow $$
$$f^{-1}(x) = \frac{5x-1}{2} $$
Para comprobar que \(f^{-1}\) es la inversa de \(f\), hay que comprobar que se cumple
$$ f^{-1}(f(x))=x, \forall x\in A$$
$$ f(f^{-1}(y)) = y, \ \forall y\in B$$
Problema 1
Determinar cuáles de las siguientes funciones tienen o no tienen inversa y por qué. No es necesario calcular la inversa:
\(f_1:\mathbb{R}\rightarrow \mathbb{R}\) definida por
$$ f_1(x) = x $$
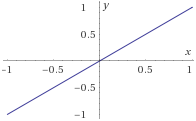
\(f_2:\mathbb{R}\rightarrow \mathbb{R}\) definida por
$$ f_2(x) = -x $$
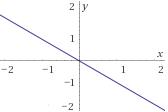
\(f_3:\mathbb{R}\rightarrow \mathbb{R}\) definida por
$$ f_3(x) = x^2 $$

\(f_4:\mathbb{R}-\{\pm 1\}\rightarrow \mathbb{R}\) definida por
$$ f_4(x) = \frac{2}{x^2-1} $$
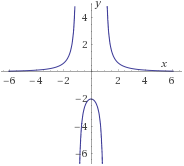
\(f_5:\left[0,+\infty \right)\rightarrow \mathbb{R}\) definida por
$$ f_5(x) = \sqrt{x} $$
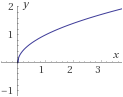
\(f_6:\ :\mathbb{R}-\{-1\} \rightarrow \mathbb{R}\) definida por
$$ f_6(x) = \frac{x^2}{x+1} $$
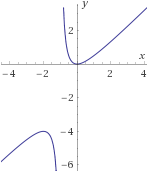
Ayuda: considerar \(f^{-1}(-1)\).
Problema 2
La biyectividad y, por tanto, la existencia de función inversa, depende de los conjuntos \(A\) y \(B\) entre los que se define una función.
Las siguientes funciones \(f:A\rightarrow B\) son sobreyectivas, pero no tienen inversa porque no son inyectivas. Encontrar, para cada función, el mayor dominio \(C\subset A\) para que las funciones \(f_{|C}\) sí tengan inversa.
$$ f_{|C}:C\rightarrow B $$
$$ f_{|C}(x) = f(x),\ \forall x\in C$$
Nota: la función \(f_{|C}\) es la función \(f\) restringida al subconjunto \(C\) del dominio \(A\) de \(f\).
Funciones:
\(f_1:\mathbb{R}\rightarrow \left[0,+\infty\right)\) definida por
$$ f_1(x) = x^2 $$

\(f_2:\mathbb{R}\rightarrow \left[0,+\infty\right) \) definida por
$$ f_2(x) = |x| $$
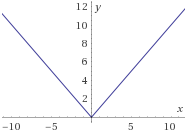
\(f_3:\mathbb{R}\rightarrow \left[-1,+\infty\right) \) definida por
$$ f_3(x) = x^2 -1$$
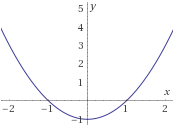
\(f_4: \mathbb{R}-\{0\}\rightarrow \left(0,+\infty\right) \) definida por
$$ f_4(x) = \frac{1}{x^2} $$
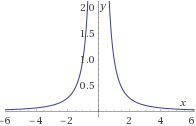
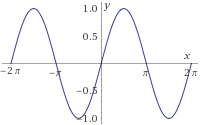
\(f_5, f_6:\left[-2\pi ,2\pi \right] \rightarrow \left[-1,1\right] \) definidas por
$$ f_5(x) = cos(x) $$
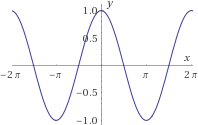
$$ f_6(x) = sin(x) $$
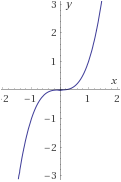
Problema 3
Encontrar la inversa de la siguiente función y demostrar (o comprobar) que lo es:
$$ f_1(x) = x^3 $$
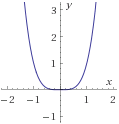
Problema 4
Encontrar la inversa de la siguiente función y demostrar (o comprobar) que lo es:
$$ f_2(x) = x^4 $$
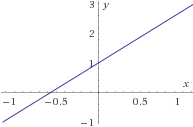
Problema 5
Encontrar la inversa de la siguiente función y demostrar (o comprobar) que lo es:
$$ f_3(x) = 1+\frac{x}{2}+\frac{2x}{3} +\frac{3x}{5} $$
Problema 6
Encontrar la inversa de la siguiente función y demostrar (o comprobar) que lo es:
$$ f_4(x) = x^2 -6x + 9 $$
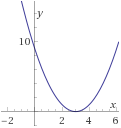
Problema 7
Encontrar la inversa de la siguiente función y demostrar (o comprobar) que lo es:
$$ f_5(x) = \frac{2}{1-3x^2} $$
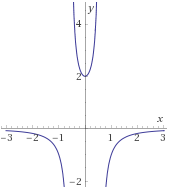
Problema 8
Encontrar la inversa de la siguiente función y demostrar (o comprobar) que lo es:
$$ f_6(x) = \sqrt{\frac{x+1}{x-1}} $$
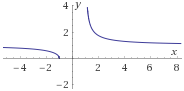
Problema 9
Relacionar las siguientes funciones
\( f_1(x) = sin(x) \)
\( f_2(x) = e^x \)
\( f_3(x) = \sqrt[3]{x}\)
\( f_4(x) = \frac{1}{x} \)
\( f_5(x) = tan(x) \)
\( f_6(x) = x \)
\( f_7(x) = \frac{1}{\sqrt{x}} \)
con su función inversa:
\( f_a (x) = x^3\)
\( f_ b(x) = arctan(x) \)
\( f_ c (x)= ln(x)\)
\( f_ d (x)= \frac{1}{x^2}\)
\( f_ e (x)= arcsin(x) \)
\( f_f (x)= 1/x\)
\( f_g (x)= x\)
Función inversa - (c) - matesfacil.com

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.