Contenido de esta página:
-
Definiciones de función par y de función impar y ejemplos.
-
Demostración de las propiedades básicas: suma, producto, composición, derivada...
En todo el texto consideraremos que las funciones están definidas sobre los reales: \(A,B,C\subseteq\mathbb{R}\).
Función par
Una función \(f:A\rightarrow B\) es par si \(f(x) = f(-x)\) para todo \(x\in A\).
Nótese que debe considerarse \(-x\in A\).
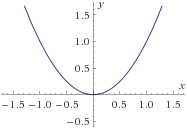
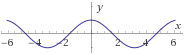
Ejemplos:
Nótese que la gráfica de una función par presenta simetría respecto del eje de las ordenadas.
Función impar
Una función \(f:A\rightarrow B\) es impar si \(f(-x) = -f(x)\) para todo \(x\in A\).
También debe considerarse \(-x\in A\).
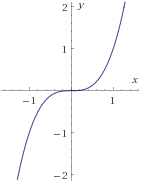
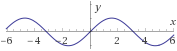
Ejemplos:
Nótese que la gráfica de una función impar presenta simetría rotacional (rotación de 180 grados).
Propiedad 1
La función constante \(f(x) = k\) es par.
Solución
Sea \(f:A\rightarrow B\) la función constante \(f(x)=k, \forall x\in A\). Es una función par ya que
$$ f(-x) = k = f(x),\ \forall x\in A $$
Propiedad 2
La suma de funciones pares es una función par.
Solución
Sean \(f:A\rightarrow B\) y \(g:A\rightarrow C\) dos funciones pares definidas sobre \(A\).
Como \(f\) y \(g\) son pares,
$$ f(-x) = f(x),\ \forall x\in A $$
$$ g(-x) = g(x),\ \forall x\in A $$
Veamos que \(f+g\) es par:
$$ (f+g)(-x) = f(-x)+g(-x) =$$
$$ = f(x) + g(x) = (f+g)(x) $$
$$\forall x\in A$$
Propiedad 3
La suma de funciones impares es impar.
Solución
Sean \(f:A\rightarrow B\) y \(g:A\rightarrow C\) dos funciones pares definidas sobre \(A\).
Como \(f\) y \(g\) son impares,
$$ f(-x) = -f(x),\ \forall x\in A $$
$$ g(-x) = -g(x),\ \forall x\in A $$
Veamos que \(f+g\) es impar:
$$ (f+g)(-x) = f(-x)+g(-x) =$$
$$ = -f(x) + -g(x) =-(f(x)+g(x))=$$
$$ = -(f+g)(x) , \ \forall x\in A$$
Propiedad 4
El producto de dos funciones pares es una función par.
Solución
Sean \(f:A\rightarrow B\) y \(g:A\rightarrow C\) dos funciones pares definidas sobre \(A\).
Como \(f\) y \(g\) son pares,
$$ f(-x) = f(x),\ \forall x\in A $$
$$ g(-x) = g(x),\ \forall x\in A $$
Veamos que \(f\cdot g\) es par:
$$ (f\cdot g)(-x) = f(-x)\cdot g(-x) =$$
$$ = f(x) \cdot g(x) = (f\cdot g)(x) $$
$$\forall x\in A$$
Propiedad 5
El producto de dos funciones impares es una función par.
Solución
Sean \(f:A\rightarrow B\) y \(g:A\rightarrow C\) dos funciones impares definidas en \(A\).
Como \(f\) y \(g\) son impares,
$$ f(-x) = -f(x),\ \forall x\in A $$
$$ g(-x) = -g(x),\ \forall x\in A $$
Veamos que \(f\cdot g\) es par:
$$ (f\cdot g)(-x) = f(-x)\cdot g(-x) =$$
$$ = (-f(x))\cdot (-g(x)) = (f\cdot g)(x) $$
$$\forall x\in A$$
Propiedad 6
La derivada de una función par es una función impar.
Solución
Debemos suponer que la función \(f:A\rightarrow B\) es derivable en \(A\).
Sea \(a\in A\).
Operamos en la definición de la derivada \(f’(-a)\) :
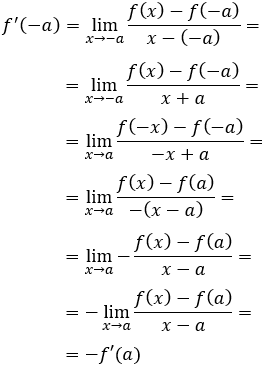
Por tanto, \(f’(-a) =- f’(a)\).
Propiedad 7
La derivada de una función impar es una función par.
Solución
Debemos suponer que la función \(f:A\rightarrow B\) es derivable en \(A\).
Sea \(a\in A\).
Operamos en la definición de la derivada \(f’(-a)\) :
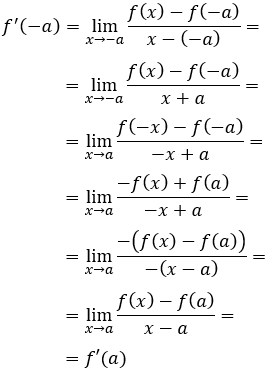
Por tanto, \(f’(-a) = f’(a)\).
Propiedad 8
La composición de dos funciones pares es una función par.
Solución
Sean \(f:A\rightarrow B\) y \(g: B\rightarrow C\) dos funciones pares.
Utilizaremos que \(f\) y \(g\) son pares:
$$ f(-x) = f(x),\ \forall x\in A$$
$$ g(-y) =g(y),\ \forall y\in B$$
Veamos que la función \( g \circ f:A\rightarrow C\) es par:
$$ (g\circ f)(-x) = g(f(-x)) =$$
$$= g(f(x)) =(g\circ f)(x), \forall x\in A$$
Propiedad 9
La composición de dos funciones impares es una función impar.
Solución
Sean \(f:A\rightarrow B\) y \(g: B\rightarrow C\) dos funciones impares.
Utilizaremos que \(f\) y \(g\) son impares:
$$ f(-x) = -f(x),\ \forall x\in A$$
$$ g(-y) =-g(y),\ \forall y\in B$$
Veamos que la función \(g\circ f:A\rightarrow C\) es impar:
$$ (g\circ f)(-x) = g(f(-x)) =$$
$$= g(-f(x)) = -g(f(x)) = $$
$$ = -(g\circ f)(x), \forall x\in A$$
Propiedad 10
Toda función definida sobre los reales, \(f:\mathbb{R}\rightarrow \mathbb{R}\), puede escribirse como la suma de una función par y una función impar.
Solución
Las funciones
$$f_1 (x) = \frac{f(x)-f(-x)}{2}$$
$$f_2 (x) = \frac{f(x)+f(-x)}{2}$$
están bien definidas, \(f_1\) es impar y \(f_2\) es par. Además, se cumple que \(f_1+f_2 = f\).