Contenido de esta página:
Introducción
Definición del espacio vectorial \(\mathbb{R}^3\) y sus propiedades
Vectores: definiciones de vector, vector libre, vector fijo, vector equipolente y vector que une dos puntos
Módulo de un vector
Producto de un escalar por un vector
Estrictamente, la geometría que se estudia en Bachillerato es la del espacio afín real tridimensional \(\mathbb{R}^3\), asociado al \(\mathbb{R}\)-espacio vectorial \(\mathbb{R}^3\). Sin embargo, como los alumnos no necesitan conocer estas tecnicidades, haremos una pequeña introducción a este espacio afín para aquellos que quieran profundizar un poco más.
En esta geometría (espacio afín real tridimensional) se trabaja básicamente con puntos y con vectores; aunque realmente los vectores son los elementos del espacio vectorial \(\mathbb{R}^3\), mientras que los puntos son los elementos del espacio ordinario \(\mathbb{R}^3\).
Por tanto, técnicamente no podemos trabajar con puntos y con vectores como elementos de la misma estructura algebraica. Sin embargo, este problema se soluciona con el concepto de espacio afín, que es un espacio que permite mezclar ambas estructuras.
Dicho de forma sencilla, el espacio afín real tridimensional es la fusión del \(\mathbb{R}\)-espacio vectorial \(\mathbb{R}^3\) y del espacio ordinario \(\mathb{R^3}\). A los elementos \(P\in\mathbb{R}^3\) los llamamos puntos y, dados dos puntos \(P\) y \(Q\) de \(\mathbb{R}^3\), llamamos vector a
$$\vec{PQ} = Q-P\in\mathbb{R}^3$$
Al vector \(\vec{AB}\) lo llamaremos vector que une a los puntos \(A\) y \(B\).
De esto modo, se pueden sumar un punto y un vector. Por ejemplo, dados los puntos \(A\), \(B\), la suma del punto \(A\) y del vector \(\vec{AB}\) es
$$ A + \vec{AB} = A + B - A = B$$
Es decir, si al punto \(A\) le sumamos el vector que une el punto \(A\) y el punto \(B\), obtenemos el punto \(B\):

En la imagen, se han representado los puntos \(A\) y \(B\), dos veces el vector \(\vec{AB}\) y el resultado de la operación \(A+\vec{AB} = B\). Nótese que el resultado de la suma de un punto \(P\neq A\) y del vector \(\vec{AB}\) es otro punto distinto a \(B\).
En esta página, estudiaremos primero la estructura del espacio vectorial real \(\mathbb{R}^3\). Después hablaremos sobre vectores: qué es un vector, un vector fijo, un vector libre, cómo calcular un vector que une dos puntos y cómo calcular el módulo de un vector.
Las operaciones entre vectores (suma, resta y productos), las trataremos a fondo en otra página.
En cada sección, se incluyen ejemplos y problemas resueltos.
El \(\mathbb{R}\)-espacio vectorial \(\mathbb{R}^3\) y sus operaciones.
Problema 1
Calcular el vector opuesto al vector \(\vec{v} = (1,2,3)\).
Problema 2
¿Por qué la suma de vectores es una operación binaria interna del espacio vectorial?
¿Por qué el producto de un escalar por un vector es una operación binaria externa del espacio vectorial?
Representaremos cada vector \(\vec{u}\) del espacio real \(\mathbb{R}^3\) como una flecha de una determinada longitud (módulo), que parte de un punto y apunta a otro punto.
Ejemplo:
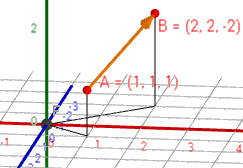
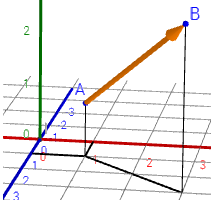
El vector une a los puntos \(A=(1,1,1)\) y \(B=(2,2,-2)\), con el sentido del punto \(A\) al punto \(B\).
La dirección del vector \(\vec{AB}\) es la recta que contiene a dicho vector.
La longitud del vector \(\vec{AB}\) se denota por \(|\vec{AB}|\) y se denomina módulo. En el ejemplo, el módulo es \(|\vec{AB}| = \sqrt{11}\).

Problema 3
Calcular el vector que une a los puntos \(A =(2,1,2)\) y \(B = (2,3,2) \) y el vector que une a los puntos \(B\) y \(A\).
Problema 4
Dado el vector libre \( \vec{v} =(-3,1,-1) \) y los puntos \(A =(1,0,4)\) y \(B =(2,0,3)\), calcular los puntos a los que apunta el vector si se traslada al punto \(A\) y al punto \(B\). Es decir, calcular \( A +\vec{v}\) y \(B+ \vec{v}\).
Nota: no es del todo correcto escribir “punto más vector” (como \( A +\vec{v}\)), puesto que no tenemos definida esta operación en el espacio. No obstante, la escribiremos para referirnos al punto que apunta un vector libre al ser trasladado a un punto concreto ya que se obtiene sumando las coordenadas del punto y las del vector.
Problema 5
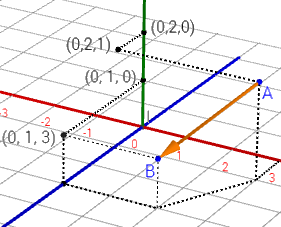
Calcular el vector libre \(\vec{v}\) que al ser trasladado al punto \(A\), une los \(A\) y \(B\) de la siguiente representación:
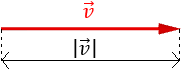
Dado el vector \(\vec{v} = (v_1, v_2, v_3)\), se define su módulo como
$$ |\vec{v} | = \sqrt{v_1^2+v_2^2+v_3^2} $$
También, podemos denotarlo por \(|| \vec{v}||\).
El módulo de un vector es su longitud.
Problema 6
Calcular el módulo de los vectores:
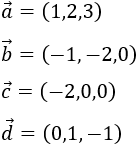
Problema 7
¿Cuál de los siguientes vectores es unitario?
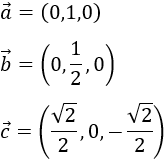
Problema 8
Normalizar los siguientes vectores:
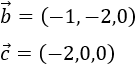
Problema 9
Preguntas para pensar:
Si dos vectores tienen el mismo módulo, ¿son vectores equipolentes?
Si dos vectores son equipolentes, ¿tienen el mismo módulo?
Sea \( \vec{u} \) el vector normalizado de \( \vec{v} \), ¿son \( \vec{u} \) y \( \vec{v} \) vectores equipolentes?
Problema 10
Demostrar las 3 propiedades del módulo de un vector enunciadas anteriormente:
El módulo de un vector es siempre no negativo.
El módulo de un vector es 0 si, y solo si, es el vector \(\vec{0} = (0,0,0)\).
Si \(\alpha \) es un escalar y \( \vec{u} = (a,b,c)\) es un vector, el módulo de \( \alpha \cdot \vec{u} = (\alpha \cdot a, \alpha \cdot b, \alpha \cdot c)\) es \(| \alpha \cdot \vec{u}| = |\alpha| \cdot | \vec{u}|\).
Sean \(\alpha \) un escalar (es decir, \( \alpha\in\mathbb{R}\)) y \( \vec{u}= (a,b,c) \) un vector (es decir, \( \vec{u}\in \mathbb{R}^3\)), entonces el producto \( \alpha \cdot u\) es el vector
$$ \alpha \cdot \vec{u}= (\alpha \cdot a, \alpha \cdot b, \alpha \cdot c) $$
Problema 11
Dados los escalares \( \alpha = 2\) y \(\beta = -3\) y los vectores \( \vec{a} = (1,-1,2)\) y \( \vec{b} = (0,-5,-3)\), calcular los productos \( \alpha \cdot \vec{a}\), \( \beta \cdot \vec{a}\), \( \alpha \cdot \vec{b}\) y \( \beta \cdot \vec{b}\).
Problema 12
Calcular el producto \(|\vec{v}| \cdot \vec{u_v}\) y comentar su resultado, siendo \( \vec{v}= (3,0,-4)\) y \(\vec{u_v}\) el vector normalizado de \( \vec{v}\).
Problema 13
Calcular el módulo del vector
$$ -0.12340845\cdot (0,3,-5)$$
Problema 14
¿Cuál es la diferencia entre los vectores \( \vec{u} \) y \( -1\cdot \vec{u} \)?
Nota: \( \vec{u} \neq (0,0,0)\).
Problema 15
Dado un vector \( \vec{u} \) no nulo, ¿cómo se obtienen los vectores que tienen el mismo sentido y dirección que \(\vec{u}\)? ¿Son todos ellos vectores equipolentes?
El espacio real tridimensional R^3 - (c) - matesfacil.com

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.