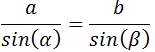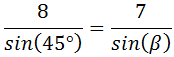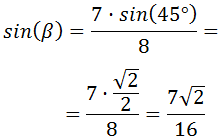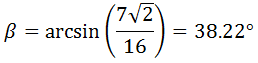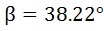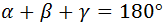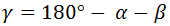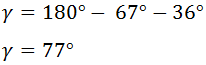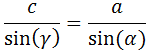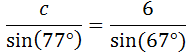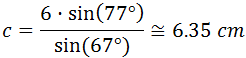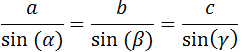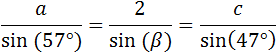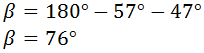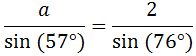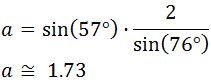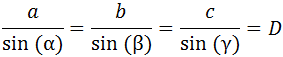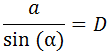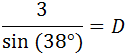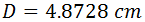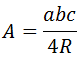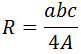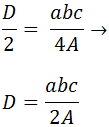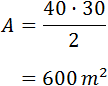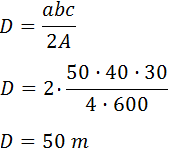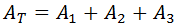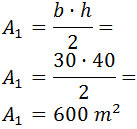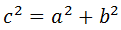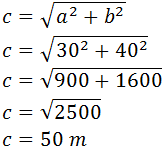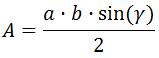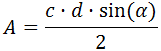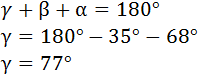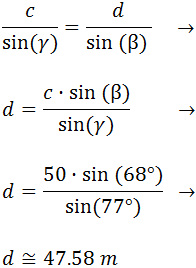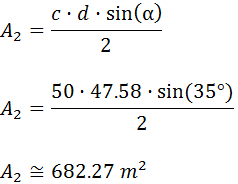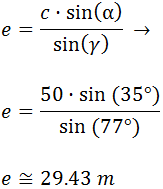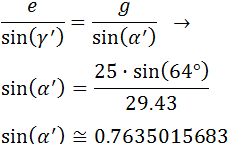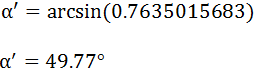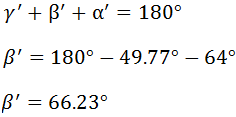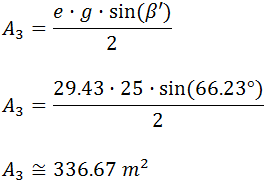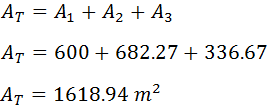Teorema del seno o de los senos
Contenido de esta página:
-
Introducción
-
Teorema del seno (enunciado y demostración)
-
Área de un triángulo inscrito (aplicación del teorema del seno)
-
7 Problemas resueltos de aplicación del teorema del seno
1. Introducción
El teorema del seno (o teorema
de los senos)
es un resultado de trigonometría que
establece la relación de proporcionalidad
existente entre las longitudes de lados de un triángulo
cualquiera con los senos de sus ángulos
interiores opuestos. Esta relación fue descubierta
en el siglo X.
Si se aplica el teorema a la fórmula del área
de un triángulo (área igual a la mitad de la base por
la altura) inscrito en una circunferencia de radio \(R\), se
obtiene una fórmula para el área en función de los lados y
del radio (apartado 3).
Para aplicar el teorema del seno se necesita conocer dos lados y
un ángulo interior (opuesto a alguno de estos dos lados), o bien,
un lado y dos ángulos (uno de ellos debe ser el opuesto al lado).
En esta página enunciamos y demostramos el teorema del seno y la fórmula
del área mencionada anteriormente y resolvemos problemas de aplicación
de éstos en los que se desea calcular algún lado, algún ángulo o el área
de algún triángulo. En algunos de los problemas se necesitan otros resultados
básicos como el teorema de Pitágoras y la propiedad de que la suma de
los ángulos internos de un triángulo es 180º.
2. Teorema del seno
Sea un triángulo cualquiera con lados \(a\), \(b\) y \(c\)
y con ángulos interiores \(\alpha \), \(\beta \) y \( \gamma \) (son los
ángulos opuestos a los lados, respectivamente).
Entonces, se cumple la relación
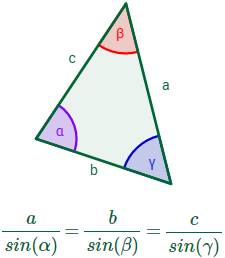
Además, se cumple
$$ \frac{a}{sin( \alpha )} = D = 2R$$
Ver demostración
Representamos el triángulo circunscrito en una circunferencia de radio
\(R\) (diámetro \(D = 2R\)) y de centro \(o\).
Representamos otro triángulo de modo que:
uno de sus lados coincide
con uno de los lados del triángulo inicial, por ejemplo,
el lado \( b\).
es un triángulo rectángulo, es decir, uno de sus ángulos mide 90º.
Para dicho ángulo, nosotros hemos escogido el
vértice donde está el ángulo \( \alpha \).
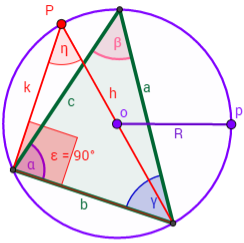
El triángulo tiene otros dos lados: \( k\) y \( h\). El lado \( h\) es su
hipotenusa y puesto que pasa por el centro de la circunferencia, mide
exactamente lo mismo que el diámetro:
$$ h = D = 2\cdot R $$
Se cumple que los ángulos \( \eta\) y \( \beta \) son iguales y, por tanto,
también lo son sus senos:
$$ sin(\eta ) = sin( \beta ) $$
Y como el nuevo triángulo es rectángulo,
$$ sin (\beta ) = sin( \eta ) = \frac{b}{h} $$
Luego
$$ h = \frac{b}{ sin( \beta )} $$
Como \( h = D = 2R\),
$$ 2R = \frac{b}{ sin( \beta )} $$
De forma similar, se obtienen las relaciones
$$ 2R = \frac{a}{ sin( \alpha )} $$
$$ 2R = \frac{c}{ sin( \gamma )} $$
de donde se concluye el teorema.
3. Área de un triángulo inscrito
Si consideramos el triángulo inscrito en una circunferencia (de radio
\( R \) y diámetro \( D = 2\cdot R\)), entonces:
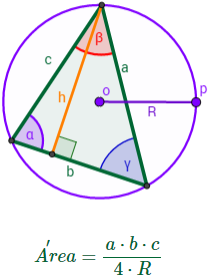
Ver demostración
Recordamos que el área de un triángulo base \(b\) y altura \( h\) es
$$ A = \frac{b\cdot h}{2} $$
Atendiendo a la representación anterior, el seno del ángulo \( \gamma \) es
$$ sin(\gamma ) = \frac{h}{a} $$
Por tanto, podemos escribir la altura, \(h\), como
$$ h = a\cdot sin(\gamma ) $$
Sustituimos esta altura en la fórmula del área:
$$ A = \frac{b\cdot a\cdot sin(\gamma )}{2} $$
Según el teorema del seno,
$$ \frac{c}{sin( \gamma )} = D = 2R$$
Luego,
$$ sin(\gamma ) = \frac{c}{2R} $$
Por tanto, la expresión del área queda como
$$ A = \frac{a\cdot b\cdot c}{4\cdot R} $$
7 Problemas Resueltos
Notas previas:
-
En el texto, escribiremos seno de
\( x\) como \(sin(x)\), aunque en otros textos lo encontraremos como
\(sen(x)\), \(seno(x)\) o \(sinus(x)\).
También utilizaremos la función
arcoseno escrita como \(arcsin\), que es la función inversa del seno. Normalmente,
en las calculadoras esta función se denota por \(sin^{-1}\).
Problema 1
En el siguiente triángulo de lados a = 8cm
y b = 7cm. Calcular
cuánto mide el ángulo β sabiendo que el ángulo γ
mide 45º.
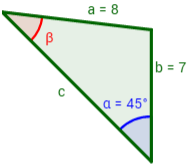
Ver Solución
Como conocemos los lados a y b y el ángulo
α, aplicamos el teorema del seno:
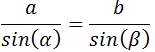
Por tanto,
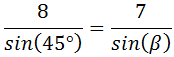
Despejamos el seno de β:
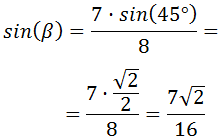
Finalmente, despejamos β utilizando la inversa del seno (arcoseno):
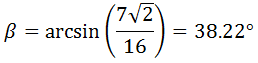
Luego el ángulo es
Problema 2
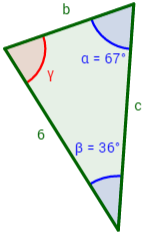
Se tiene un triángulo con ángulos α = 67° y β = 36° y un lado
a = 6cm. ¿Cuánto mide el lado c?
Ver Solución
Para calcular el lado c necesitamos conocer el ángulo γ.
Recordemos que en todo triángulo la suma de sus ángulos
internos es 180°, es decir, tenemos la ecuación:
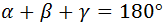
Despejamos el ángulo γ:
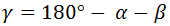
Sustituimos los valores:
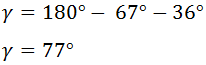
Luego el ángulo es γ = 77º.
Ahora podemos aplicar el teorema del seno:
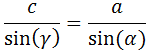
Sustituimos los datos:
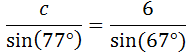
Por tanto,
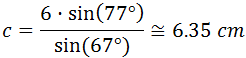
Luego el lado c mide 6.35 cm.
Problema 3
En el siguiente triángulo con lado b = 2cm y ángulos α = 57° y γ = 47°, ¿cuánto mide el lado a?
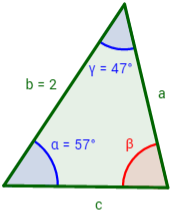
Ver Solución
Por el teorema del seno,
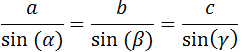
Sustituimos en dicha relación los datos proporcionados:
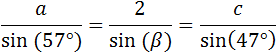
Tal como están escritas las relaciones, no podemos calcular el
lado a porque nos faltan datos. Pero como la suma de
los ángulos debe ser 180º, podemos calcular el ángulo β:
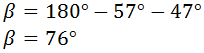
Ahora ya podemos obtener el lado a:
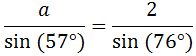
De donde
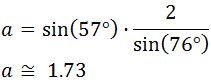
Luego el lado a mide 1.73 cm.
Problema 4
Calcular el radio y el diámetro de la circunferencia
sobre el que está inscrito el siguiente triángulo conociendo el único ángulo
α = 38°.
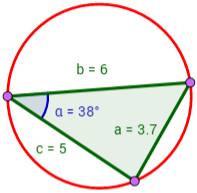
Ver Solución
El teorema del seno nos proporciona el diámetro de
la circunferencia:
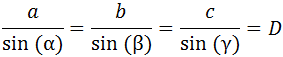
Los valores de los lados b y de c y de sus
respectivos ángulos opuestos β y α no son
necesarios a la hora de calcular el diámetro ya
que podemos servirnos únicamente de la relación
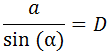
Sustituimos los valores en la fórmula:
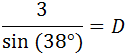
Por tanto, el diámetro de la circunferencia es
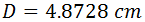
Problema 5
En un vecindario con forma circular, viven David,
Pedro y Fernando. Sus casas están en las
orillas de la vecindad. Sabemos que entre la
casa de David y la de Pedro hay 50 metros, entre la casa de
Pedro y Fernando hay 30 metros y entre la casa de Fernando y
la de David hay 40 metros. ¿Cuál es el diámetro de
la vecindad donde viven si las distancias forman
un triángulo rectángulo?
Ver Solución
El diagrama del vecindario es un triángulo rectángulo de lados
40m, 50m y 30m inscrito en una circunferencia:
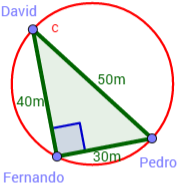
Nota: la distancia mayor debe ser necesariamente la
hipotenusa del triángulo.
Al aplicar el teorema del seno a la fórmula del área de un
triángulo se obtiene que ésta es
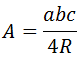
Primero, despejamos R en la fórmula:
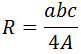
Puesto que el diámetro es dos veces el radio, \( D = 2R\), se tiene
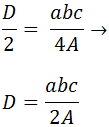
Como disponemos de los valores de los lados a,
b y c, para obtener el
radio, R, sólo necesitamos calcular el
área y sustituirla en la fórmula anterior.
Al ser el triángulo rectángulo, su base y su altura coinciden con
sus dos catetos. Esto nos proporciona el área:
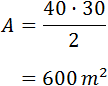
Para terminar, sustituimos todos los valores en la fórmula del
diámetro que obtuvimos:
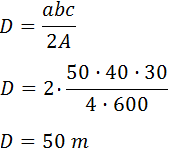
Luego el diámetro de la vecindad es de 50 metros.
Problema 6
Se quiere construir un centro comercial con la siguiente forma:
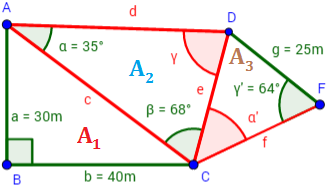
Si sabemos que los lados a, b y g medirán 30 metros,
40 metros y 25
metros respectivamente, y los ángulos medirán
α = 35°, β = 68° y γ'= 64°, ¿cuál será el área total
del centro comercial?
Ver Solución
Debemos calcular el área de los tres triángulos para obtener el
área total, es decir:
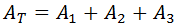
Puesto que el primer triángulo (el de vértices A,
B y C) es rectángulo, su
base, b, y su altura, h,
coinciden con sus catetos. Luego su
área es
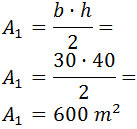
Además, puesto que este triángulo es rectángulo, podemos
aplicar el teorema de Pitágoras
para calcular su hipotenusa (lado c):
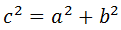
Sustituyendo los valores de a y b y
calculando la raíz cuadrada, obtenemos c:
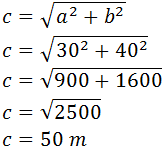
Para calcular el área del segundo
triángulo (el de vértices A, D y
C), utilizaremos una de las
fórmulas del área obtenida al aplicar el teorema del seno:
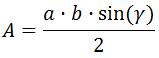
Es decir, necesitamos conocer dos lados
(por ejemplo, c y d) y el
ángulo opuesto al otro lado (el
ángulo opuesto al lado e, que es α):
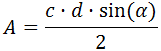
Conocemos el lado c, pero no el d. Tenemos que calcularlo:
Como conocemos los valores de dos de los ángulos
(α y β), podemos calcular el ángulo
γ porque sabemos que la suma de los
tres ángulos debe ser 180º:
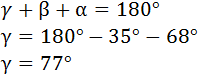
Ahora que conocemos todos los ángulos del segundo
triángulo, podemos calcular el lado d. Para
ello, aplicamos el teorema del seno:
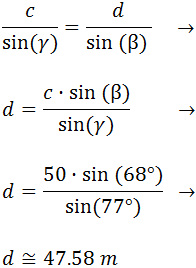
Calculamos el área \( A_3 \):
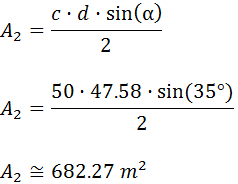
Finalmente, para calcular el área del último
triangulo aplicaremos la misma fórmula.
Necesitamos conocer dos lados (por
ejemplo, e y g) y el
ángulo opuesto al otro
lado (el opuesto a f).
Primero debemos calcular el lado e.
Aplicando el teorema del
seno (en el segundo triángulo):
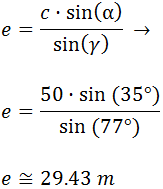
Como conocemos los lados e y g y el
ángulo γ', podemos calcular el ángulo α':
Cuantos más decimales escribimos, más buena será
la aproximación del ángulo:
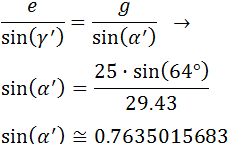
Aplicando el arcoseno,
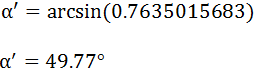
Ahora ya podemos calcular el ángulo β'
(el tercer ángulo del tercer triángulo)
puesto que conocemos los otros dos ángulos del triángulo:
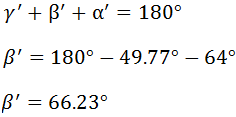
Calculamos el área del tercer triángulo:
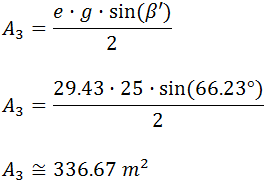
Para terminar, debemos sumar las tres áreas
calculadas. Luego el área del centro comercial es
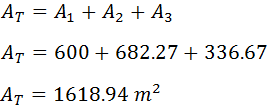


Teorema del seno o de los senos: demostración y problemas resueltos -
(c) -
matesfacil.com

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.