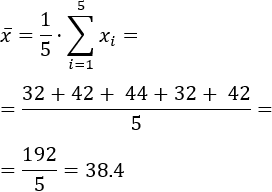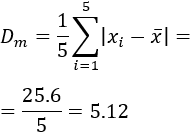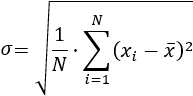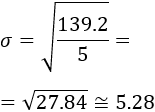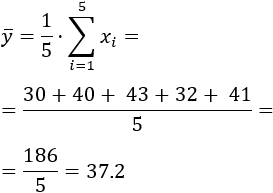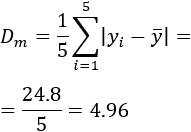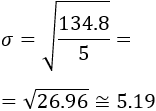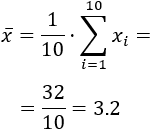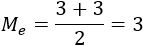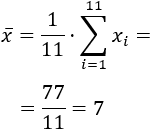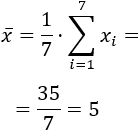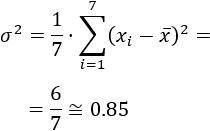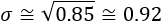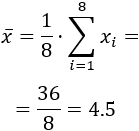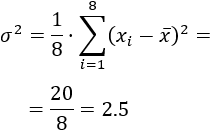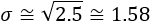Parámetros de centralización y de dispersión
Contenido de esta página:
- Introducción.
- Ejemplo introductorio.
- Parámetros de centralización: media, moda y mediana.
- Parámetros de dispersión: desviación respecto de la media, desviación media, varianza y desviación típica (o estándar).
- Ejercicios resueltos: cálculo e interpretación de los parámetros.
1. Introducción
Un parámetro de una población es una medida que resume o describe el comportamiento general de dicha población. En ocasiones, como en el caso de las poblaciones pequeñas, se pueden observar todos los datos y, por tanto, su comportamiento, pero esto no siempre es así. Es entonces cuando sobre todo nos interesan estas medidas ya que nos permiten conocer cómo se distribuyen los datos sin necesidad de conocerlos todos.
En esta página explicamos el significado de algunos parámetros (de centralización y de dispersión), cómo calcularlos y los calcularemos en distintas poblaciones pequeñas (problemas resueltos).
Tabla resumen

Los parámetros se clasifican, básicamente, en parámetros de centralización, dispersión, forma y posición según el tipo de información que proporcionan.
Como curiosidad, cuando las poblaciones son muy grandes (como todos los individuos de un país) no podemos calcular los parámetros de un modo exacto. Entonces, utilizamos los llamados estadísticos, que son aproximaciones de los parámetros que se calculan a partir de una muestra más o menos pequeña y representativa de la población total.
Existen estadísticos para cada parámetro. Por ejemplo, la media muestral \(\overline{x}\) es un estadístico que se obtiene a partir de una muestra de la población. Este estadístico es una aproximación de la media \(\mu\) de la población.
2. Ejemplo introductorio
Supongamos que queremos estudiar la altura (en centímetros) de un grupo de 10 alumnos de un aula:
165, 170, 175, 173, 169,
183, 171, 176, 172, 170
Si observamos todos los datos, encontramos alturas muy cercanas (como 170, 171, 172 y 173) y otras muy lejanas (como 165 y 183). Pero podemos decir, por simple observación, que la mayoría ronda o se aproxima a los 173cm.
En estadística, esta altura aproximada se denomina media y se calcula sumando todas las alturas y dividiendo el resultado entre el número total de alturas (es el promedio o la media aritmética).
Calculamos la media de las alturas del ejemplo:
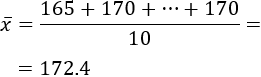
La altura media de los alumnos es 172.4 centímetros. Este dato es un parámetro de la población estudiada.
Hay otros aspectos que nos importan de la población, por ejemplo:
- ¿Cuál es la altura que más se repite?
- ¿Hay más alturas por debajo de la media o por encima?
- ¿Hay mucha diferencia entre las alturas y la altura media?
Existen parámetros que responden a estas cuestiones.
Continuaremos con el ejemplo de las alturas (visto en la sección 2) para explicar los siguientes parámetros: media, moda, mediana, desviación respecto de la media, desviación media, varianza y desviación típica.
3. Parámetros de centralización
Son las medidas que informan acerca de la mayor o menor agrupación o concentración de los datos entorno a la media: media, moda y mediana.
Ejemplos:
- Las alturas del ejemplo se agrupan alrededor de 172.4cm. Este valor es la media.
- La altura que más se repite es 170cm (dos veces). Este valor es la moda.
- Si ordenamos las alturas, la que ocupa la posición central se denomina mediana. Más tarde veremos cómo se calcula.
Media
El parámetro media es la media aritmética o promedio de todos los datos. Se calcula sumando todos los datos y dividiendo el resultado entre el número total de datos (\(N\)):
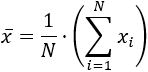
Explicamos los elementos que intervienen en la fórmula:
- La letra \(N\) es el número total de datos (en nuestro ejemplo, \(N = 10\)).
-
El sumatorio (dentro del paréntesis) significa que debemos sumar los \(x_i\) desde \(i = 1\) hasta \( i = N\):
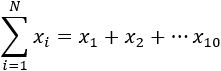
-
Cada \(x_i\) es un dato de la población. En el ejemplo de las alturas, los \(x_i\) son:
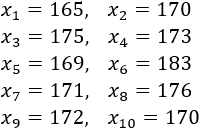
La media ya la hemos calculado en el ejemplo introductorio:
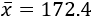
Nota técnica: utilizamos la notación \(\overline{x}\) para referirnos a la media de la población, pero generalmente se utiliza para denotar la media de una muestra de la población. Para la media real (generalmente desconocida) se utiliza \(\mu\). No obstante, en nuestro caso podemos utilizar ambas ya que trabajaremos con la población total.
Moda
La moda es el dato que más se repite. En nuestro ejemplo, la moda es 170 (se repite dos veces).
Si hay dos datos que se repiten el mismo número de veces, se dice que la distribución es bimodal (hay dos modas).
Si hay más de dos datos que se repiten el mismo número de veces (por ejemplo, si se repiten cinco alturas), la distribución es multimodal.
Si todos los datos se repiten el mismo número de veces, entonces no hay moda. Si ningún dato se repite, tampoco hay moda.
Mediana
Si ordenamos los datos de mayor a menor, la mediana es el dato o datos centrales (según si hay un número par o impar).
Si el número de datos es impar, el que ocupa la posición central es la mediana:
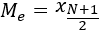
Si el número de datos es par, hay dos datos centrales. Entonces, los sumamos y dividimos el resultado entre dos:
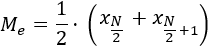
Los datos de nuestro ejemplo, ordenados de menor a mayor, son
165, 169, 170, 170, 171,
172, 173, 175, 176, 183
Tenemos dos datos centrales: 171 y 172 (el quinto y el sexto). Los sumamos y dividimos:
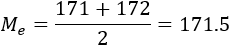
4. Parámetros de dispersión
Son los parámetros que indican la mayor o menor concentración de los datos alrededor de los parámetros de centralización: desviación respecto de la media, desviación media, varianza y desviación estándar.
Desviación respecto de la media
Hemos dicho que la media es el dato al que se aproximan más o menos todos los datos. Pero esta aproximación no tiene porqué ser la misma en cada dato.
Si tomamos un dato, \(x_i\), su desviación respecto de la media \(\overline{x}\) es la diferencia entre ellos (en valor positivo). Es decir,
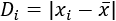
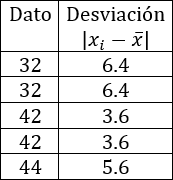
Calculamos la desviación de los datos \(x_1=169\) y \(x_9 = 172\) respecto de la media:
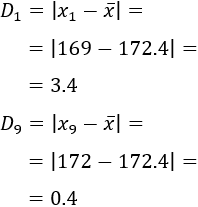
Cuanto mayor es la desviación de un dato, más se aleja de la media.
Desviación media
La desviación media es la media de todas las desviaciones respecto de la media. Es decir, se suman todas las desviaciones (hay \(N\)) y se divide entre el número de datos (\(N\)):
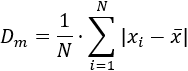
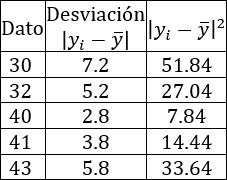
Calculamos las desviaciones y la desviación media de nuestro ejemplo:
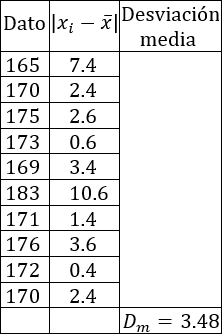
La desviación media es 3.18. La traducción de este dato es que la media de las diferencias de cada altura con la altura media es 3.18cm.
Si la desviación media es muy grande, entonces las alturas de los alumnos varían mucho de la media. Mientras que si es muy pequeña, varían poco.
Ejemplo:
La media de los datos 0, 0, 5, 10, 10 es 5. Pero la media de los datos 5, 5, 5, 5, 5 también es 5. Sin embargo, la diferencia entre la primera muestra y la segunda es significativa: en la primera, la mayoría de los datos distan mucho de la media, mientras que en la segunda todos los datos coinciden con la media.
Esta diferencia en la distribución de los datos es importante y no se refleja en la media, pero sí se refleja en la desviación media: en la primera, \(D_m = 4\) y en la segunda, \(D_m = 0\).
La variancia y la desviación típica son parámetros similares a los de desviación respecto de la media y desviación media, pero se calculan de otra forma. También nos informan de la dispersión de los datos respecto de la media.
Varianza
La varianza o variancia se denota por \(\sigma^2\) o por \(s^2\) y puede calcularse de dos formas. La primera de ellas es la media aritmética de los cuadrados de las deviaciones de los datos respecto de la media:
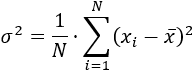
La otra forma de calcularla es
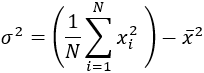
Desviación estándar
La desviación típica (o desviación estándar) se denota por \(\sigma\) o por \(s\) y es la raíz cuadrada de la varianza:
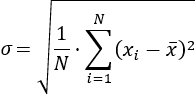
O bien,
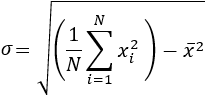
Comentarios
A lo largo del texto hemos visto distintos parámetros. Algunos nos informan, más o menos, del mismo aspecto de la distribución de los datos. Por ejemplo, la media y la mediana son parámetros parecidos (de centralización), pero la media es muy sensible a los datos extremos y la mediana no. También, hemos visto que dos poblaciones pueden tener la misma media pero ser muy distintas cuando tienen una desviación media distinta.
En definitiva, un estudio estadístico correcto debe contemplar un gran número de parámetros y estudiarlos en conjunto para determinar el comportamiento de la población.
Problemas Resueltos
Problema 1
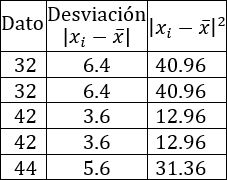
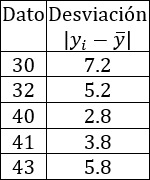
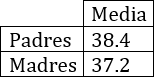
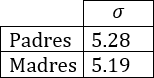
Cinco amigos han escrito en una tabla las edades de sus padres:
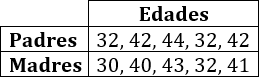
Se pide:
- Calcular la media, moda, mediana, desviación media y desviación típica de las edades de los padres (varones).
- Hacer lo mismo con las edades de las madres.
- En general, ¿son más mayores los padres o las madres?
- ¿Las edades que se alejan más de la media son las de los padres o las de las madres?
Problema 2
El número de bolígrafos que llevan en el estuche un grupo de alumnos son
3, 4, 2, 5, 3,
3, 4, 2, 2, 4
Se pide:
- Calcular la media y la mediana de los datos (grupo de 10).
Recientemente, se une un alumno al grupo. Este nuevo individuo tiene un estuche que consta con una colección de 45 bolígrafos de colores.
- Calcular la media y la mediana de los datos incluyendo al nuevo individuo (grupo de 11).
- Sacar conclusiones del comportamiento de la media y de la mediana.
Problema 3
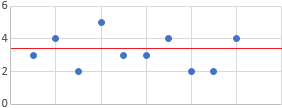
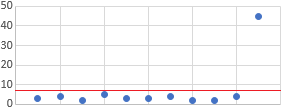
Las siguientes gráficas recogen el tiempo de espera (en minutos) de las líneas telefónicas de atención al cliente de dos compañías de telefonía.
Compañía A:
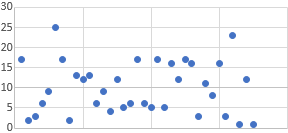
Compañía B:
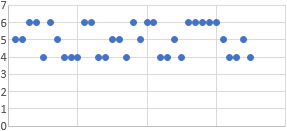
Observando las gráficas,
- Calcular una aproximación del tiempo medio de espera en ambas compañías.
- ¿En cuál de las dos compañías es mayor la desviación estándar?
- Si realizamos 5 llamadas a cada una de las compañías, ¿en cuál de ellas el tiempo de espera de las 5 llamadas será parecido?
Problema 4
El profesor de matemáticas ha escrito una tabla con los datos de las notas de sus alumnos del aula A y del aula B:
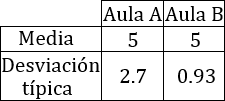
Aunque la nota media en ambas aulas es 5 (aprobado),
- ¿En qué aula parece que el rendimiento de los alumnos es similar? ¿Por qué?
- ¿En qué aula parece que hay notas más altas? ¿Por qué?
Problema 5
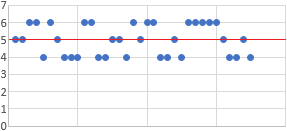
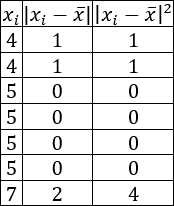
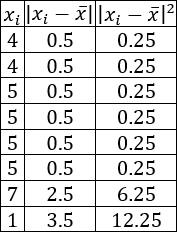
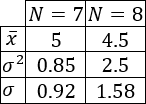
La siguiente tabla recoge las notas de 7 alumnos en la asignatura Matemáticas:

Se pide:
- Calcular la varianza y la desviación estándar.
El profesor había olvidado un examen en la carpeta. Lo corrige y añade la nota a la tabla (es un 1):

- Calcular la varianza y la desviación estándar añadiendo el nuevo dato.
- Según los resultados, ¿es más sensible la varianza o la desviación estándar?
Parámetros de centralización y de dispersión - (c) - matesfacil.com

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.