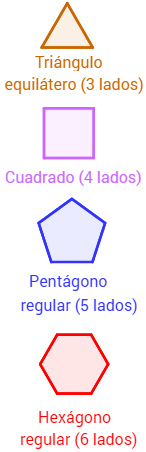
Polígonos |
Contenido de esta página:
-
Conceptos básicos: definición y ejemplos.
-
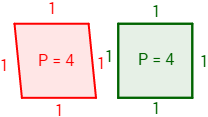
Elementos de un polígono: vértice, diagonal, centro, apotema, perímetro y semiperímetro.
-
Test en línea sobre los conceptos anteriores.
1. Conceptos básicos
Concepto, clasificación y ejemplos.
2. Elementos de un polígono
Lado, vértice, diagonales, apotema, perímetro y semiperímetro.
3. Test sobre polígonos
Escoger la opción correcta en cada pregunta.
Pregunta 1
Un hexágono es un polígono con seis lados. ¿Cuántos vértices tiene un hexágono?
|
5 vértices
|
|
|
6 vértices
|
|
|
12 vértices
|
Pregunta 2
El número de vértices de un polígono de \(n\) lados es...
|
\(n\)
|
|
|
\(n+1\)
|
|
|
\(n\) si es un polígono regular y \(n+1\) si es irregular
|
Razonamiento:
Pregunta 3
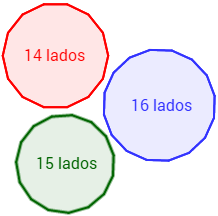
¿Cuántos lados tiene un pentadecágono?
|
14 lados
|
|
|
15 lados
|
|
|
16 lados
|
Razonamiento:
Pregunta 4
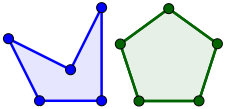
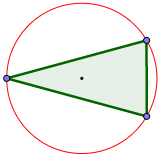
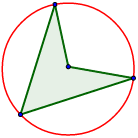
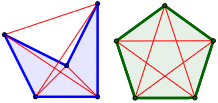
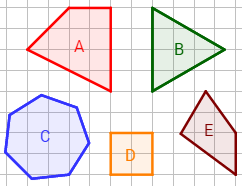
¿Cuáles de los siguientes polígonos son regulares?
|
Los polígonos B, D y E son regulares.
|
|
|
Los polígonos B, C y D son regulares.
|
|
|
Ninguno de los polígonos es regular.
|
Pregunta 5
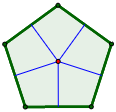
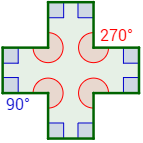
¿Cuál es el perímetro de un dodecágono irregular cuyos lados miden 1 m?

|
12 cm
|
|
|
13cm
|
|
|
23 cm
|
Observando la representación anterior, ¿sabrías decir por qué el dodecágono es irregular si todos sus lados miden lo mismo?
Razonamiento:
Para pensar:
¿Podemos saber si un polígono es regular fijándonos sólo en los lados exteriores?
Pregunta 6
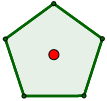
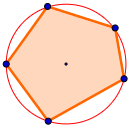
Un polígono está inscrito en una circunferencia cuando todos sus vértices están sobre ella. Por ejemplo, el siguiente pentágono regular está inscrito en una circunferencia:
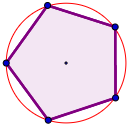
¿Cuándo es posible inscribir un polígono en una circunferencia?
|
Sólo cuando el polígono es regular.
|
|
|
Siempre.
|
|
|
Depende del polígono.
|
Razonamiento:
Pregunta 7
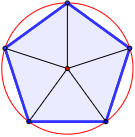
Un polígono regular puede ser inscrito en una circunferencia cuando...
|
El número de vértices es par.
|
|
|
El número de vértices es impar. |
|
|
Siempre.
|
Razonamiento:
Pregunta 8
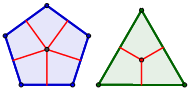
En un polígono regular...
|
Todas las apotemas miden lo mismo.
|
|
|
No todas las apotemas miden lo mismo.
|
|
|
Las apotemas miden lo mismo solamente cuando el polígono tiene más de 5 lados.
|
Razonamiento:
Pregunta 9
¿Cuántas diagonales tiene un trígono?
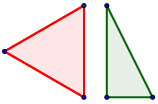
|
Ninguna.
|
|
|
Dos.
|
|
|
Tres.
|
Razonamiento:
Pregunta 10
¿Cuántas diagonales tiene un decágono?
|
30.
|
|
|
35.
|
|
|
305.
|
Razonamiento:
Pregunta 11
¿Cuántos grados mide cada ángulo (interior) de un polígono regular de \(n\) lados?
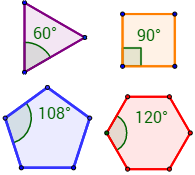
|
$$\frac{180\cdot (n-2)}{n}$$
|
|
|
$$\frac{360 \cdot (n-2)}{n}$$
|
|
|
$$\frac{360 \cdot n}{n-2}$$
|
Razonamiento:
Pregunta 12
Si dos polígonos tienen el mismo número de lados y el mismo perímetro, ¿son iguales?
|
Sí.
|
|
|
No.
|
Razonamiento:
Pregunta 13
Si dos polígonos regulares tienen el mismo número de lados y el mismo perímetro, ¿son iguales?
|
Sí.
|
|
|
No.
|
Razonamiento:
Polígonos: elementos y test en línea - (c) - matesfacil.com

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.