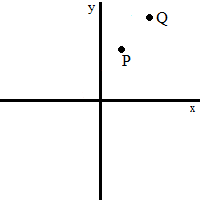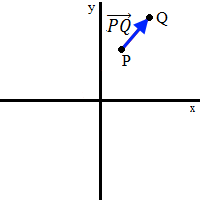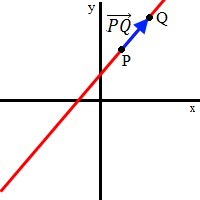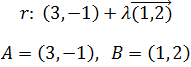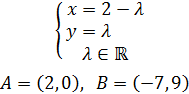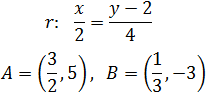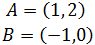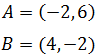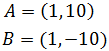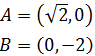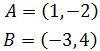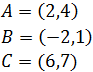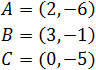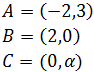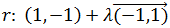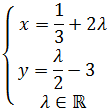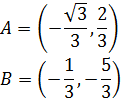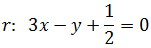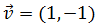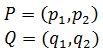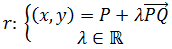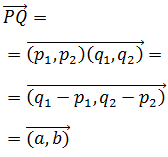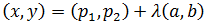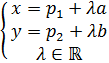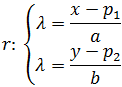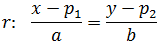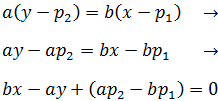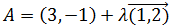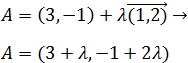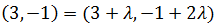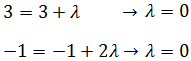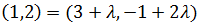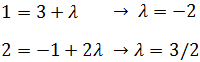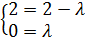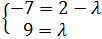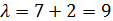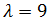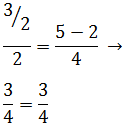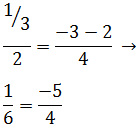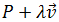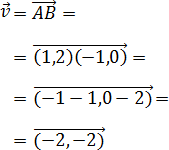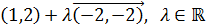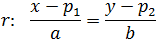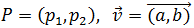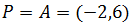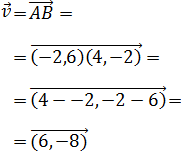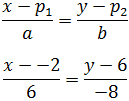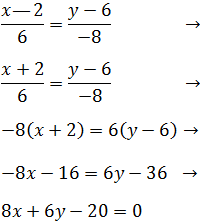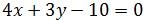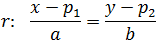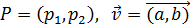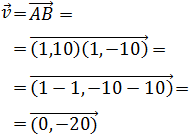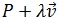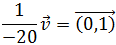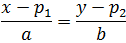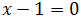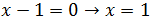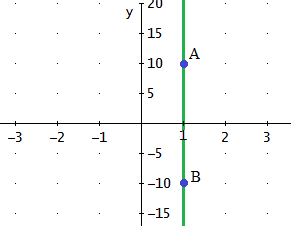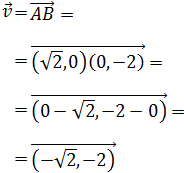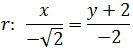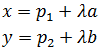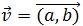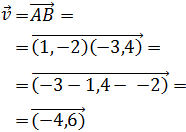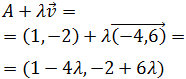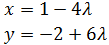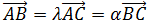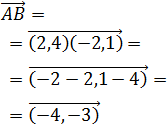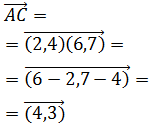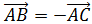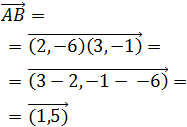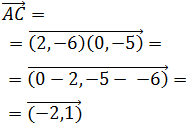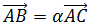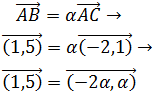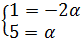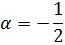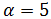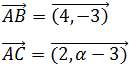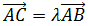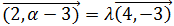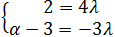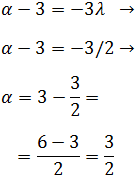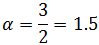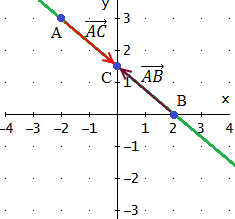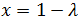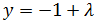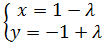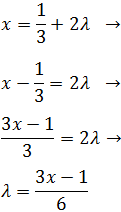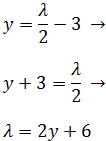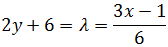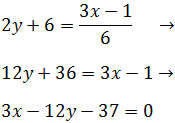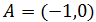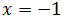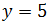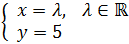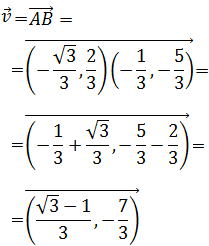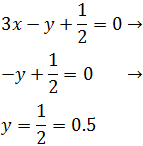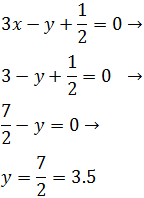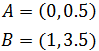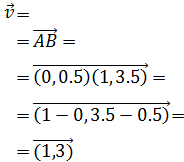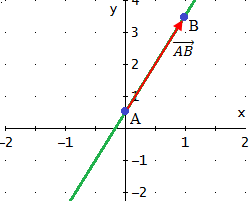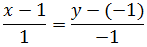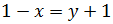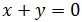Ecuaciones de la Recta en el Plano Real
|
Contenido de esta página:
Ecuación Vectorial
$$ P + \lambda \overrightarrow{PQ}$$
donde P y Q son dos puntos de la recta y
$$ \overrightarrow{PQ} $$
representa el vector que va de P a Q.
Si P = (p1 , p2 ) y
Q = (q1 , q2 ), entonces
$$ \overrightarrow{PQ} = \overrightarrow{(q_1 - p_1,\ q_2 - p_2)} $$
A estos vectores que se obtienen a partir de dos puntos de la recta les denominamos
vectores directores.
Ecuaciones Paramétricas
Sea P = (p1 , p2 ) un punto de la recta y
$$ \overrightarrow{v} = \overrightarrow{(a,\ b)} $$
un vector director de la recta, llamamos ecuaciones
paramétricas de la recta a
$$
\begin{equation*}
\left\lbrace
\begin{array}{l}
x = p_1 + \lambda a \\
y = p_2 + \lambda b \\
\end{array}
\right.
\end{equation*}
$$
siendo λ un parámetro real.
Obtenemos los puntos de la recta dando valores al parámetro λ.
Ecuación Continua
$$ \frac{x-p_1}{a} = \frac{y-p_2}{b}$$
donde P = (p1 , p2 ) es un punto de la recta y
$$ \overrightarrow{v} = \overrightarrow{(a,\ b)} $$
un vector director de la recta.
Nota: esta ecuación no puede usarse cuando alguna de las coordenadas
del vector director es 0 (a = 0 ó b = 0) ya que no podemos dividir por 0.
Ecuación Implícita
Es de la forma
$$ ax + by + k = 0 $$
siendo a, b y c números que tenemos que determinar.
Normalmente, obtendremos esta ecuación operando sobre la ecuación
continua de la recta.
Teoría:
Obtención de las Ecuaciones
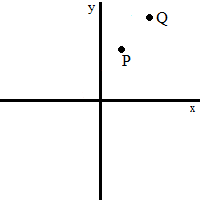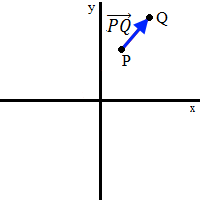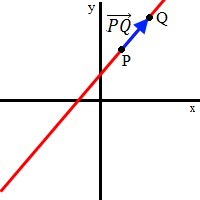
Ver Teoría
Ecuación Vectorial:
Un recta queda determinada por dos de sus puntos.
Si los unimos, tenemos un segmento que forma parte de la recta
y, por tanto, podemos alargar este segmento para
convertirlo en una recta (segmento de longitud infinita).
Sean dos puntos de la recta r:
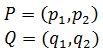
Entonces los puntos de r pueden expresarse mediante
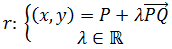
Es la llamada ecuación vectorial de la recta r.
Dando valores al parámetro λ podemos obtener todos los puntos de r.
Como vemos en la ecuación anterior, si tenemos un punto y
el vector director de la recta (vector que se obtiene a
partir de dos puntos de la recta) también podemos
obtener dicha ecuación. Es decir, la podemos obtener
a partir de dos puntos (distintos)
o de un punto y un vector director.
Ecuaciones Paramétricas:
Llamaremos a las componentes del vector (a, b), es decir,
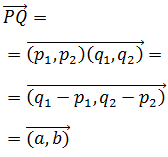
Entonces, la ecuación vectorial queda como
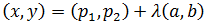
Separando cada coordenada:
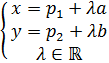
Estas son las llamadas ecuaciones paramétricas de la recta r.
Ecuación Continua:
Notemos que en ambas ecuaciones (en las paramétricas) tenemos el parámetro λ. Podemos despejarlo
en ambas ecuaciones e igualarlas:
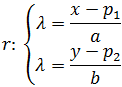
Siempre que a, b ≠ 0.
Igualando el parámetro λ obtenemos la ecuación
continua de la recta r:
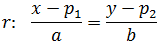
Ecuación Implícita:
A partir de la ecuación anterior podemos expresar y en función de x como:
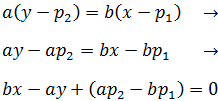
Esta última expresión es la llamada ecuación implícita de la recta.
Problemas Resueltos
Problema 1
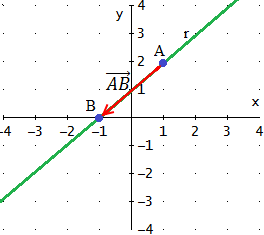
Dada la siguiente ecuación vectorial de la recta r, comprobar
si los puntos A y B son puntos de r:
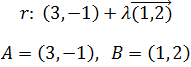
Ver Solución
Si los puntos están en la recta, tienen que cumplir su ecuación, es decir,
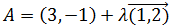
para algún valor del parámetro λ.
Sumando los vectores tenemos:
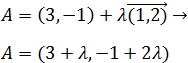
Conociendo A, tenemos que
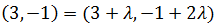
De donde obtenemos las dos ecuaciones
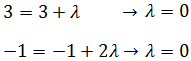
Como hemos obtenido el mismo valor para λ, el punto sí
forma parte de la recta.
Para B procedemos del mismo modo:
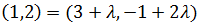
Es decir,
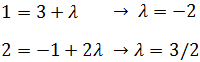
Como los valores para λ son distintos, el punto B no
pertenece a la recta.
Problema 2
Dadas las siguientes
ecuaciones paramétricas de la recta r, comprobar si los
puntos A y B son puntos de r
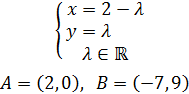
Ver Solución
Si el punto A está en la recta, tiene que verificar las ecuaciones.
Entonces,
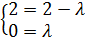
De ambas ecuaciones obtenemos que λ = 0, por lo que el punto A
sí pertenece a la recta.
Procedemos de igual modo para el punto B:
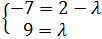
De la primer ecuación obtenemos que
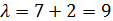
Y de la segunda
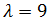
Puesto que los valores para λ coinciden, el punto B
sí pertenece a la recta.
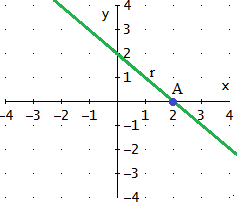
Problema 3
Dada la siguiente ecuación continua
de la recta r, comprobar si los puntos A y B son puntos de r
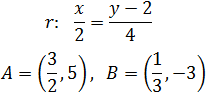
Ver Solución
Si el punto A forma parte de la recta, entonces tiene que
cumplirse la ecuación:
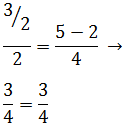
Obtener una igualdad verdadera significa que el punto cumple la ecuación
y, por tanto, está en la recta.
De forma análoga para B:
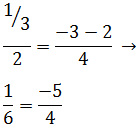
Obtenemos una igualdad falsa, por lo que el punto B no cumple la
ecuación y, por ende, no forma parte de la recta.
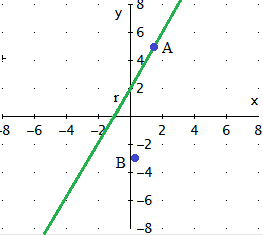
Problema 4
Dados los puntos A y B de una recta r, encontrar la
ecuación vectorial de r
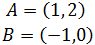
Ver Solución
La ecuación vectorial es
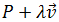
donde P y Q son dos puntos de la recta, λ un
parámetro real y v un vector director de la recta.
Podemos obtener el vector como
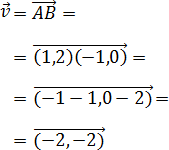
El punto P puede ser cualquier punto de la recta.
Escogemos P = B.
Por tanto, la ecuación vectorial de la recta es
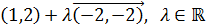
Problema 5
Dados los puntos A y B de una recta r, encontrar
la ecuación implícita de r
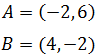
Ver Solución
La ecuación implícita de la recta la podemos obtener
rápidamente a partir de la ecuación continua
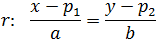
donde
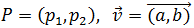
son un punto de la recta y un vector de la recta, respectivamente.
Podemos considerar el punto
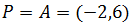
Y el vector
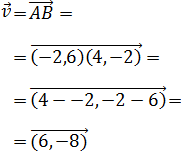
Una vez tenemos el punto P y el vector v
tenemos que sustituir sus componentes en la forma continua de la recta:
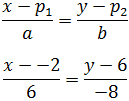
Ahora operamos hasta llegar a la ecuación en forma implícita:
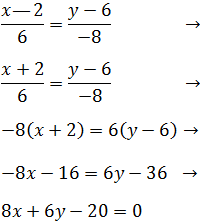
La última ecuación es la buscada, pero podemos dividir
la ecuación por 2 para disminuir los coeficientes:
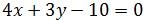
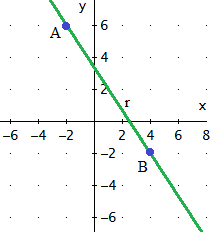
Problema 6
Dados los puntos A y B de la recta r, encontrar
la ecuación implícita de r
Ver Solución
La ecuación implícita de la recta la podemos obtener
rápidamente a partir de la ecuación continua
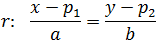
donde
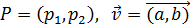
son un punto de la recta y un vector de la recta, respectivamente.
Podemos considerar el punto
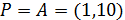
Y el vector
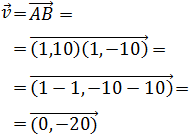
Puesto que los vectores sólo nos indican la inclinación de la recta,
podemos trabajar con sus múltiplos. De hecho, sabemos que
obtenemos todos los puntos de la recta si vamos dando valores
al parámetro λ en la ecuación vectorial:
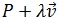
Entonces, trabajaremos con
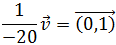
para evitar los números grandes.
Una vez tenemos el punto P y el vector director v
tenemos que sustituir sus componentes en la forma continua de la recta:
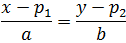
Sin embargo, tenemos un problema ya que la primera componente del vector
es a = 0 y no podemos dividir por 0.
Una forma muy sencilla de solucionar el problema es usar la ecuación
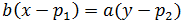
obtenida a partir de la ecuación continua.
Sustituimos los valores:
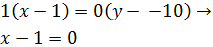
Por tanto, la ecuación implícita de la recta es
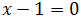
Nota: en esta ecuación no aparece la variable y.
Esto se debe a que la recta es vertical y, por tanto,
los puntos de la recta son todos los que tienen en la primera
coordenada un 1:
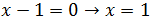
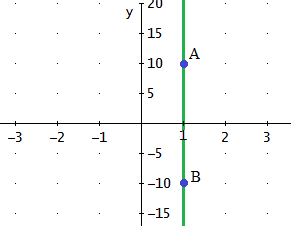
Problema 7
Dados los puntos A y B de una recta r, encontrar
la ecuación continua de r
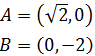
Ver Solución
Un vector director es
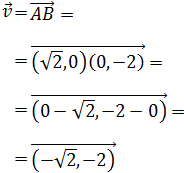
Por tanto, usando el punto B y el vector v la ecuación continua de la recta es
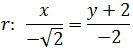
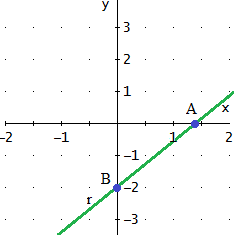
Problema 8
Dados los puntos A y B de una recta r, encontrar
las ecuaciones paramétricas de r
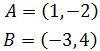
Ver Solución
Las ecuaciones paramétricas de la recta son de la forma
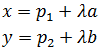
siendo λ el parámetro y
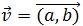
un vector director.
Podemos usar el vector director que une a ambos puntos:
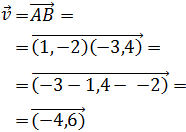
Usando el punto A y el vector anterior podemos obtener
la recta en forma vectorial:
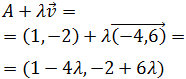
Ahora, usamos las coordenadas para escribir las ecuaciones paramétricas:
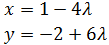
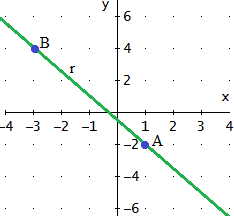
Problema 9
Comprobar si los tres puntos A, B y C determinan una recta en
el espacio bidimensional
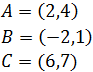
Ver Solución
Lo que tenemos que comprobar es que los puntos están alineados.
Si es así, los vectores que unen a los tres puntos serán
proporcionales, es decir, linealmente dependientes,
dicho matemáticamente:
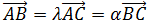
Es suficiente comprobarlo con dos de los vectores:
El vector que une los puntos A y B es
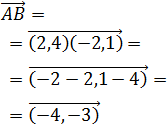
Y el vector que une los puntos A y C es
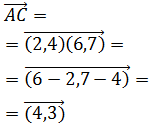
Notemos que
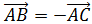
Por tanto, existe una recta que une a los tres puntos A,
B y C.
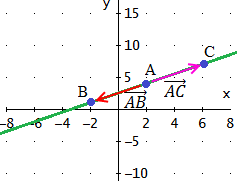
Problema 10
Comprobar si los tres puntos A, B y C determinan una recta
en el plano real:
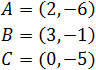
Ver Solución
Procedemos como en el ejercicio anterior: calculamos dos vectores
que unan a los puntos y comprobaremos si son
proporcionales (linealmente dependientes):
El vector que une los puntos A y B es
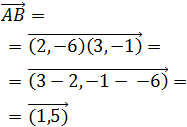
El vector que une los puntos A y C es
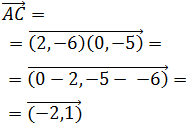
Vamos a ver que no existe ningún valor para
α de modo que se cumpla que
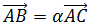
ya que
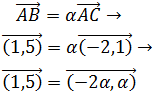
Tenemos el sistema de ecuaciones:
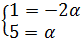
De la primera ecuación tenemos que
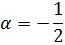
Y de la segunda
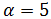
Es decir, multiplicando por α el vector sólo podemos
hacer que coincida una de los dos coordenadas,
pero no las dos.
Por tanto, los vectores no son proporcionales,
con lo que los puntos no están alineados y no
pueden estar en la misma recta.
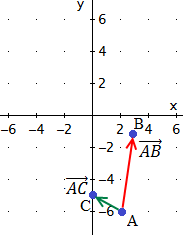
Problema 11
Encontrar el valor del parámetro α para que el punto C
esté en la recta que une los puntos A y B
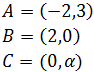
Ver Solución
Tenemos que buscar el valor de α para que los tres
puntos estén alineados.
Los vectores que unen los puntos A con B y A
con C son
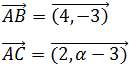
Queremos que
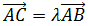
Para algún valor de λ.
Por tanto,
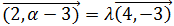
Obtenemos las dos ecuaciones
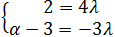
De la primera ecuación tenemos que λ = 1/2.
Sustituimos en la segunda ecuación:
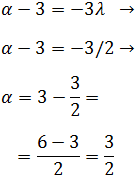
Por tanto,
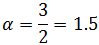
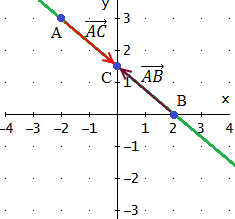
Problema 12
Dada la siguiente ecuación vectorial de la recta r, obtener las
ecuaciones paramétricas de dicha recta
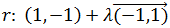
Ver Solución
De la ecuación anterior sabemos que la primera coordenada de los puntos es
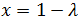
Y la segunda coordenada es
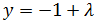
Por tanto, las ecuaciones paramétricas son
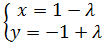
Problema 13
Dadas las siguientes ecuaciones paramétricas de la recta r, obtener la
ecuación implícita de dicha recta
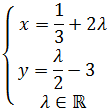
Ver Solución
Despejamos en ambas ecuaciones el parámetro λ.
En la primera ecuación:
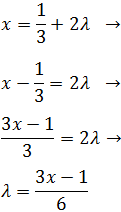
En la segunda ecuación:
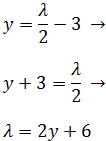
Ahora igualamos las dos ecuaciones:
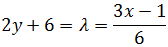
Por tanto,
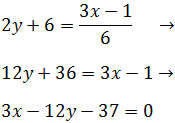
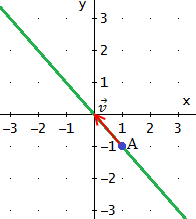
Problema 14
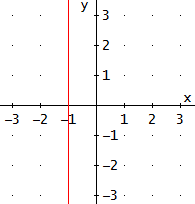
Obtener la ecuación en forma implícita de la recta vertical
que pasa por el punto A = ( -1 , 0 ).
Ver Solución
Como la recta es vertical, todos los puntos tienen
la misma primera coordenada.
Sabemos que uno de sus puntos es
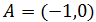
Por tanto, todos los puntos tienen la primera coordenada x = -1.
La expresión
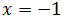
es justamente la ecuación en forma implícita de la recta.
Problema 15
Obtener las ecuaciones paramétricas de la recta horizontal que pasa
por el punto A = ( 5 , 5 ).
Ver Solución
Como la recta es horizontal, la segunda coordenada
de todos sus puntos es la misma.
Puesto que el punto A es uno de sus puntos,
sabemos que la segunda coordenada es
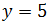
Por tanto,
Las ecuaciones paramétricas de la recta son
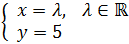
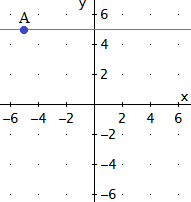
Problema 16
Encontrar un vector director de la recta que pasa por
los puntos A y B
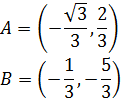
Ver Solución
Un vector director de la recta es cualquiera que una dos
puntos de la recta:
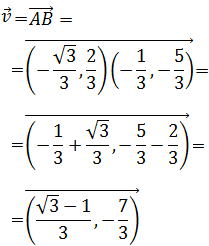
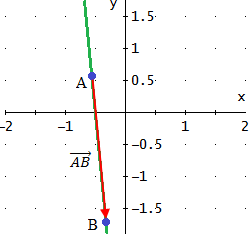
Problema 17
Encontrar un vector director de la recta r cuya ecuación
implícita es
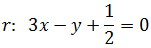
Ver Solución
Un vector director lo podemos obtener a partir de dos
puntos de la recta, por lo que vamos a tomar dos puntos que cumplan
la ecuación (entonces pertenecen a la recta) y calcular el
vector que los une:
Si x = 0, entonces la segunda coordenada es
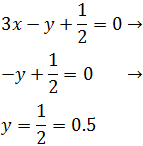
Si x = 1, entonces la segunda coordenada es
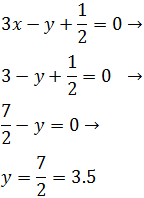
Por tanto, dos puntos de la recta son
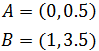
El vector que los une es
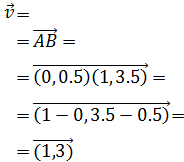
Problema 18
Encontrar la ecuación implícita de la recta que pasa por el punto
A = ( 1 , -1 ) y su vector director es
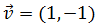
Ver Solución
La obtendremos a partir de la ecuación continua:
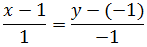
De donde
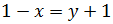
Por tanto, la ecuación implícita es
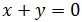
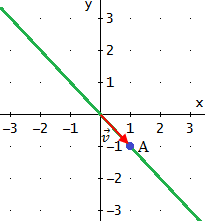

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.