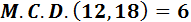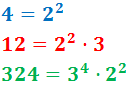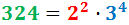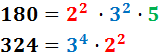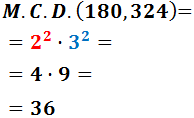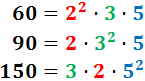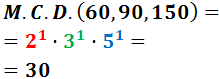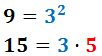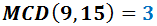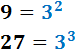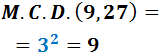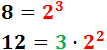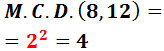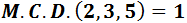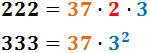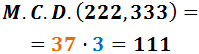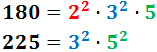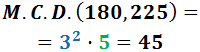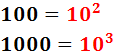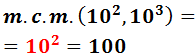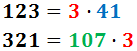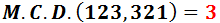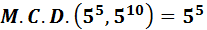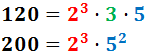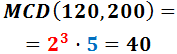Máximo Común Divisor:Teoría y Ejercicios Resueltos |
Contenido de esta página:
-
Concepto de Máximo Común Divisor (MCD)
-
Descomposición en números primos (recordatorio)
-
Método para la obtención del MCD a partir de la descomposición
-
Test y Ejercicios resueltos: calcular el MCD de dos o tres números, preguntas teóricas y problemas de aplicación
1. Definición y Ejemplo
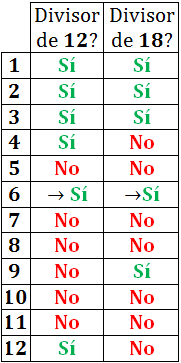
El máximo común divisor de dos números a y b es el número más grande que divide a a y divide a b.
Para denotar el máximo común divisor de a y b escribiremos M.C.D.(a, b) ó MCD(a, b).
2. Descomposición en Números Primos
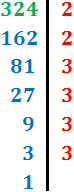
Vamos a recordar cómo descomponer números para escribirlos como un producto de números primos, lo cual facilitará el cálculo del máximo común divisor:
3. Obtención del MCD a partir de las descomposiciones
Regla para el MCD:
«comunes al menor exponente»
4. El MCD de más de dos números
Ejercicios Resueltos de Máximo Común Divisor: Test y Problemas
Ejercicio 1
El máximo común divisor de 9 y 15 es...
Escoger la opción correcta:
|
9, porque el MCD no puede ser mayor que los números
|
|
|
1, porque divide a los dos números
|
|
|
3, porque es el mayor divisor de los números
|
Razonamiento:
Ejercicio 2
El máximo común divisor de 9 y 27 es...
|
3, porque 9 y 27 son potencias de 3
|
|
|
9, porque divide a 9 y a 27 y su MCD debe ser menor o igual que 9 y que 27
|
|
|
27, porque es el MCD debe ser máximo
|
Razonamiento:
Ejercicio 3
El máximo común divisor de 2, 3 y 4 es...
|
1, porque es no hay otro divisor común de 2 y de 3
|
|
|
12, porque es múltiplo de los tres números
|
|
|
2, porque es el MCD debe ser menor o igual que 2, 3 y 4
|
Razonamiento:
Ejercicio 4
El máximo común divisor de 8 y 12 es...
|
1
|
|
|
4
|
|
|
8
|
Razonamiento:
Ejercicio 5
El máximo común divisor de 2, 3 y 5 es...
|
0
|
|
|
1
|
|
|
6
|
Razonamiento:
Ejercicio 6
El máximo común divisor de 222 y 333 es...
|
111
|
|
|
222
|
|
|
333
|
Razonamiento:
Ejercicio 7
El máximo común divisor de 180 y 225 es...
|
12
|
|
|
45
|
|
|
85
|
Razonamiento:
Ejercicio 8
El máximo común divisor de 100 y 1000 es...
|
10
|
|
|
100
|
|
|
1000
|
Razonamiento:
Ejercicio 9
El máximo común divisor de 123 y 321 es...
|
2
|
|
|
3
|
|
|
123
|
Razonamiento:
Ejercicio 10
El máximo común divisor de 55 y 510 es...
|
55
|
|
|
510
|
|
|
515
|
Razonamiento:
Ejercicio 11
El máximo común divisor de dos números primos es...
|
1
|
|
|
El número primo menor.
|
|
|
El producto de los números primos.
|
Razonamiento:
Ejercicio 12
El máximo común divisor es 0 cuando...
|
Uno de los dos números es primo pero el otro no.
|
|
|
Los dos números son potencia de la misma base.
|
|
|
Nunca.
|
Razonamiento:
Ejercicio 13
El máximo común divisor de dos números...
|
Es múltiplo de los dos números.
|
|
|
Es siempre un número par.
|
|
|
Es menor o igual que los dos números.
|
Razonamiento:
Ejercicio 14
Si el máximo común divisor de dos números es el 4...
|
Los dos números son una potencia de 2.
|
|
|
Al menos uno de los números es una potencia de 2.
|
|
|
Los dos números son pares.
|
Razonamiento:
Ejercicio 15
Si el máximo común divisor de dos números es impar, entonces...
|
Los dos números son impares.
|
|
|
No podemos deducir la paridad de los números,
es decir, pueden ser pares, impares o uno par y otro impar.
|
|
|
No pueden ser pares los dos números, es decir, o los dos son impares o uno es par y el otro es impar.
|
Razonamiento:
Ejercicio 16
Tenemos una cuerda de 120 metros y otra de 200 metros. Se desea cortarlas para obtener otras cuerdas, todas de la misma longitud pero lo más largas posibles, de modo que no sobre ningún trozo.
Calcular la longitud de las cuerdas y el número total de cuerdas.
== Ayuda: ==
Ejemplo 1: podemos cortar la de 200m obteniendo una de 120m y una de 80m. Pero esta elección no es correcta ya que no miden todas lo mismo.
Ejemplo 2: si cortamos en cuerdas de 1m, todas medirán lo mismo pero serán demasiado cortas.
Ejercicio 17 (dificultad alta)
Consideremos el MCD de dos números a y b.
Si los números a y b son divisibles por el número primo k (distinto del MCD), entonces...
|
k es divisible por el MCD.
|
|
|
el MCD es divisible por k.
|
|
|
No existe relación de divisibilidad entre k y el MCD.
|
Razonamiento:
Ejercicio 18 (dificultad alta)
El MCD de dos números pares...
|
También es par.
|
|
|
Es impar.
|
|
|
No existe relación.
|
Razonamiento:

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.