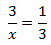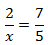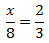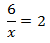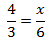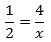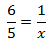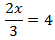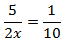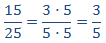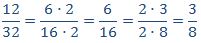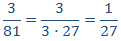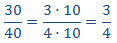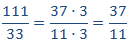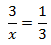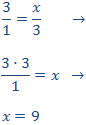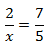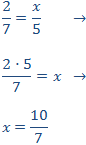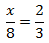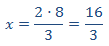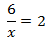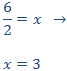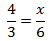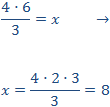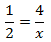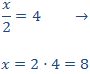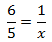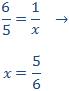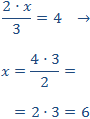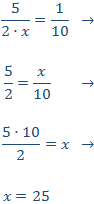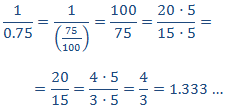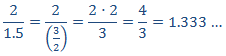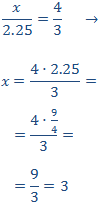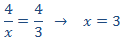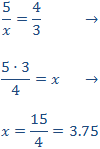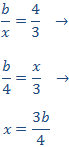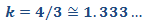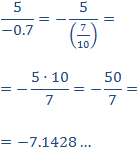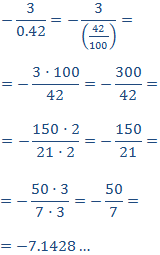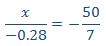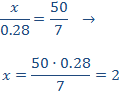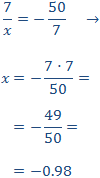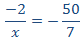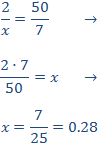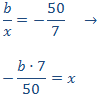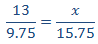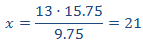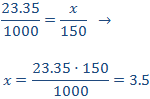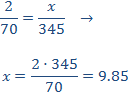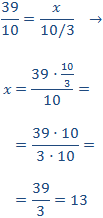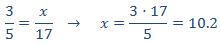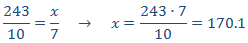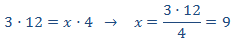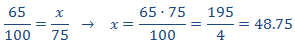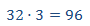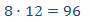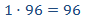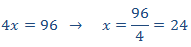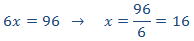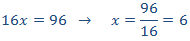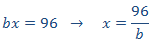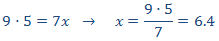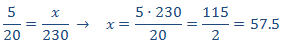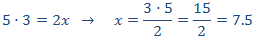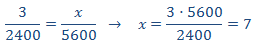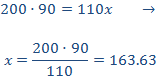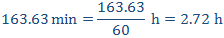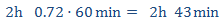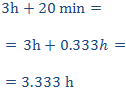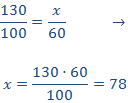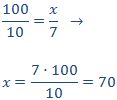Proporcionalidad simple directa e inversa |
Contenido de esta página:
Enlace: Calculadora de porcentajes.
Introducción
Proporcionalidad directa:
Dos magnitudes \(a\) y \(b\) son directamente proporcionales
cuando existe una constante \(k\) tal que
$$ \frac{a}{b} = k$$
La constante \(k\) se denomina constante
de proporcionalidad o razón.
Se dice que \(a\) y \(b\) mantienen una
relación de proporcionalidad directa.
En este tipo de proporcionalidad, cuando una de las magnitudes aumenta, la otra también; y lo mismo ocurre
cuando alguna de las dos disminuye.
Ejemplo:
En un movimiento con velocidad constante \(v\), la distancia
recorrida viene dada por la ecuación
$$ distancia = v \cdot tiempo $$
La distancia es directamente proporcional al tiempo puesto que
$$ \frac{distancia}{tiempo} = v $$
En este ejemplo, la velocidad es la constante de proporcionalidad.
Cuando el tiempo aumenta, la distancia también lo hace y
viceversa.
Regla de tres (directa)
Si dos magnitudes \(a\) y \(b\)
mantienen una relación de proporcionalidad directa, una regla de tres simple directa (o simplemente regla de
tres directa) nos permite conocer el valor de una de las dos magnitudes cuando la otra varía.
Para aplicar una regla de tres, escribimos la siguiente tabla:
+ |
Valor |
Valor |
Magnitud \(a\) |
\(a_1\) |
\(a_2\) |
Magnitud \(b\) |
\(b_1\) |
\(b_2\) |
Como la relación de proporcionalidad directa debe ser constante, ha de cumplirse que
$$ \frac{a_1}{b_1} = \frac{a_2}{b_2}$$
De esta relación podemos despejar el valor que deseamos calcular.
Proporcionalidad inversa:
Dos magnitudes \(a\) y \(b\) son inversamente proporcionales
cuando existe una constante \(k\) tal que
$$ a\cdot b= k $$
La constante \(k\) se denomina constante
de proporcionalidad.
En esta proporcionalidad, cuando una de las magnitudes aumenta, la otra disminuye y viceversa.
Ejemplo:
Si un trabajador pinta una valla en 10 horas, entonces para pintar la misma valla entre dos trabajadores se necesitan 5 horas.
Se trata de una proporcionalidad inversa puesto que cuando aumenta el número de trabajadores, el número de horas necesarias disminuye. La constante de proporcionalidad es 10 porque
$$ 1\cdot 10 =10 =2\cdot 5 $$
Es decir, si \(a\) es el número de trabajadores y \(b\) el número de horas, entonces
$$ a\cdot b = 10$$
Regla de tres (inversa)
Cuando dos magnitudes \(a\) y \(b\) mantienen
una relación de proporcionalidad inversa, una regla de
tres simple inversa (o simplemente regla de tres
inversa) nos permite conocer el valor de una de las dos magnitudes
cuando la otra varía.
Para aplicar una regla
de tres, escribimos la siguiente tabla:
- |
Valor |
Valor |
Magnitud \(a\) |
\(a_1\) |
\(a_2\) |
Magnitud \(b\) |
\(b_1\) |
\(b_2\) |
Como
la relación de proporcionalidad indirecta debe ser constante, se cumple que
$$ a_1\cdot b_1 = a_2\cdot b_2$$
De esta relación podemos despejar el valor que deseamos calcular.
Nota: en ocasiones se utilizan los signos (+) y (-) en las tablas
escritas anteriormente para denotar que se trata de una proporcionalidad directa
e indirecta, respectivamente.
16 Problemas Resueltos
Primero se calculan razones entre dos números y reglas de tres.
Después, problemas en los que hay que
encontrar la relación de proporcionalidad y aplicar una
regla de tres, ya sea directa o inversa.
Problema 1
Calcular la razón de los números
-
15 y 25
12 y 32
3 y 81
30 y 40
111 y 33
Ver solución
La razón es el cociente de los números.
Escribiremos los números como productos
para simplificar las fracciones rápidamente
15 y 20
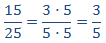
12 y 32
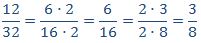
-
3 y 81
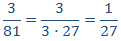
30 y 40
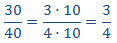
111 y 33
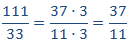
Problema 2
Calcular el valor de la incógnita en cada una de las relaciones de proporcionalidad:
Nota: por ejemplo, la igualdad
$$ \frac{3}{7} = \frac{18}{42} $$
significa que la razón de los números 3 y 7 es la misma que la
razón de los números 18 y 42. Es decir, la relación de proporcionalidad
es la misma.
Ver solución
Tenemos que aislar la x. Los factores que están multiplicando en un lado de la
igualdad pasan al otro lado dividiendo y viceversa.
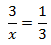
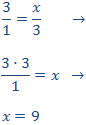
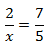
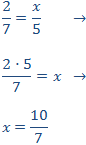
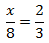
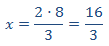
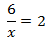
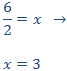
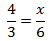
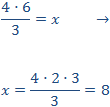
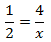
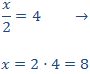
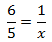
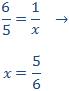
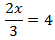
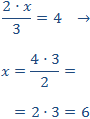
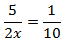
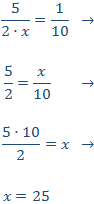
Problema 3
Completar la tabla para que las magnitudes de la primera fila sean directamente proporcionales a las de la segunda e indicar cuál es la
constante de proporcionalidad.

Ver solución
En la primera columna tenemos (recordamos que 0.75 = 75/100):
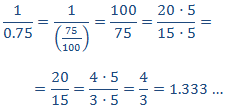
Por tanto, la primera razón es 20/15=1.333…
En la segunda columna tenemos (recordamos que 1.5 = 3/2):
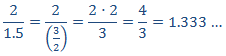
La razón tiene que ser 4/3 en todas las columnas.
Llamamos x al hueco de la columna 3
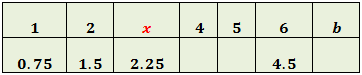
Recordamos que 2.25 = 9/4
Queremos que se cumpla la relación
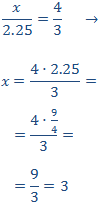
Ahora llamamos x al hueco de la columna 4:
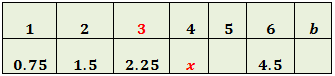
Queremos que se cumpla la relación
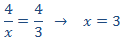
Ahora llamamos x al hueco de la quinta columna:
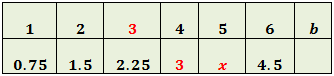
Queremos que se cumpla la relación
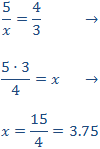
Finalmente, llamamos x al hueco de la última columna

En este caso, la diferencia es que el número es un parámetro (un número que no conocemos), pero se procede de igual modo. Queremos que se cumpla la relación
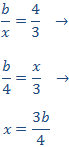
Por tanto, la tabla resultante es

La constante de proporcionalidad de la tabla (es decir, la razón que
se repite en todas las columnas) es
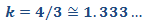
Problema 4
Completar la tabla para que las magnitudes de la primera fila sean directamente proporcionales a las de la segunda e indicar cuál es la
constante de proporcionalidad.

Ver solución
Calculamos la razón de la primera columna (recordamos que 0.7 = 7/10):
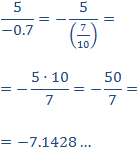
Notemos que es un número negativo.
La razón de la segunda columna es (recordamos que 0.42=42/100):
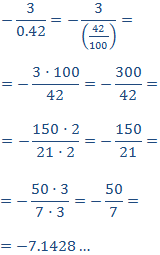
Obtenemos la misma razón, que es la constante de proporcionalidad de la tabla.
Buscamos los 4 números que faltan igual que hicimos en el ejercicio anterior:
Columna 3:
Llamamos x al hueco de la columna 3

Queremos que se cumpla la relación
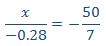
Como los dos lados de la igualdad son negativos, podemos quitar el signo:
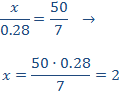
Llamamos x al hueco de la columna 4
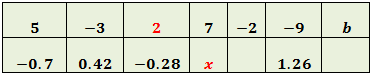
Queremos que se cumpla la relación
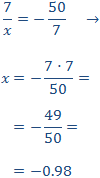
Ahora llamamos x al hueco de la quinta columna

Queremos que se cumpla la relación
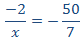
Como tenemos un signo negativo en los dos lados de la igualdad, podemos quitarlo:
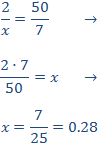
Finalmente, llamamos x al hueco de la última columna

En este caso, el número es un parámetro (un número que no conocemos), pero se procede de igual modo. Queremos que se cumpla la relación
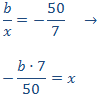
Por tanto, la tabla resultante es

Notemos que en cada columna hay un número positivo y otro negativo. De este modo, el cociente (la razón) siempre es negativo.
La constante de proporcionalidad de la tabla (es decir, la razón
que se repite en todas las columnas) es
$$-\frac{50}{7} \simeq -7.1428$$
Problema 5
El precio de un paquete de 13 rotuladores es de 9.75€.
¿Cuántos rotuladores podemos comprar con un presupuesto de 15.75€?
Ver solución
Aplicaremos una regla de tres:
Se trata de una relación de proporcionalidad directa: cuantos más rotuladores compramos, mayor es el precio total.
Llamamos x al número de rotuladores que queremos comprar y que desconocemos:
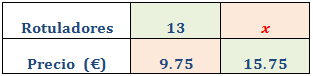
Como es proporcionalidad directa, aplicamos una regla de tres directa:
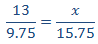
Despejamos la x:
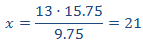
Hemos pintado las celdas en forma de aspa ya que podemos obtener la fórmula anterior directamente multiplicando los dos recuadros verdes y dividiendo entre el rojo (el que
no tiene la x).
Por tanto, podemos comprar 21 rotuladores por el precio total de 15.75€.
Problema 6
José marca 5 goles cada 25 minutos de partido. Calcular mediante una regla de tres cuántos goles marcará en una hora. Indicar si es una proporcionalidad directa o inversa.
Ver solución
Se trata de una proporcionalidad directa: cuanto más minutos, más goles marcará.
Llamamos x al número de goles que marcará en una hora.
Tengamos en cuenta que el tiempo hay que expresarlo en la misma unidad de tiempo (minutos, por ejemplo), por lo que escribimos 60 minutos en lugar de una hora.
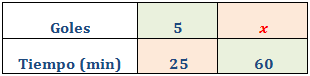
Como es proporcionalidad directa, aplicamos una regla de tres directa:

Por tanto, esperamos que José marque 12 goles en una hora.
Problema 7
El precio por kilo de queso azul es de 23.35€.
¿Cuánto nos costarán 150g de queso? Indicar si es una proporcionalidad directa o inversa.
Ver solución
Se trata de una proporcionalidad directa: cuanto más queso, más caro.
Como tenemos que usar la misma unidad de peso, escribimos 1000g en vez de 1kg.
Llamamos x al precio que buscamos:
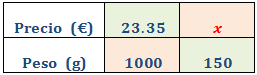
Como es proporcionalidad directa, aplicamos una regla de tres directa:
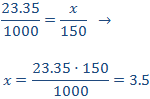
Por tanto, el precio de 150g de queso es de 3.5€
Problema 8
Un autobús recorre 70km en dos horas. ¿Cuánto tardará en realizar un viaje de 345km? Indicar si es una proporcionalidad directa o inversa.
Ver solución
Se trata de un problema de proporcionalidad directa: cuanto mayor es la distancia, mayor es el tiempo.
Llamamos x al tiempo que buscamos:
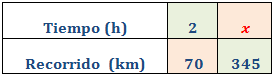
Como es proporcionalidad directa, aplicamos una regla de tres directa:
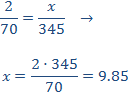
El autobús tardará aproximadamente (porque hemos redondeado) 9.8 horas, es decir, casi 10 horas.
Problema 9
La puntuación de Sandra (sobre 10) en un
examen de matemáticas de 39 preguntas es 3.3333...
puntos. ¿Cuántas preguntas ha contestado correctamente?
Ver solución
Se trata de una proporcionalidad directa: cuantas más respuestas correctas, más puntuación.
Notemos que si contestamos correctamente todas las preguntas, la puntuación será la máxima,
es decir, 10.
Llamamos x al número de respuestas correctas.
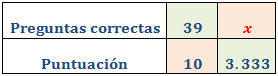
Podemos escribir 3.333… como 10/3.
Como es una proporcionalidad directa, aplicamos una regla de tres directa:
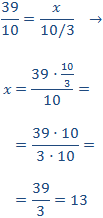
Ha contestado 13 preguntas correctamente.
Problema 10
Si tardamos 3 horas en estudiar los 5 primeros temas del examen,
¿cuántas horas más necesitamos para terminar de estudiar si en total hay 17 temas?
Ver solución
Se trata de una proporcionalidad directa: cuantos más temas, más tiempo se necesita.
Llamamos x al tiempo que queremos calcular:

Como es una proporcionalidad directa, aplicamos una regla de tres directa:
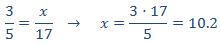
Por tanto, tardaremos 10.2 horas en estudiar los 17 temas. Como ya hemos estudiado
3 horas, necesitamos estudiar 7.2 horas más.
Problema 11
Para obtener el certificado de inglés se necesita obtener un 7 sobre 10 en un test de 243 preguntas. Calcular el número mínimo de preguntas correctas necesarias para obtenerlo.
Ver solución
Proporcionalidad directa: cuantas más respuestas correctas, más puntuación.
Llamamos x al número de preguntas:
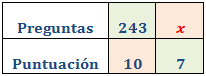
Como es una proporcionalidad directa, aplicamos una regla de tres directa:
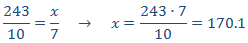
Por tanto, obtenemos un 7 si hay 170.1 respuestas correctas, es decir, se requieren al menos 171 para obtener el certificado.
Problema 12
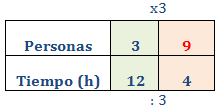
Tres personas tardan 12 horas en pintar un muro. ¿Cuántas personas se necesitan si se quiere finalizar la tarea en tan solo 4 horas?
Ver solución
Es una proporcionalidad inversa: cuantos más trabajadores, menos tiempo.
Llamamos x al número de personas:
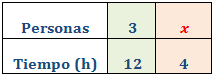
Como es una proporcionalidad inversa, aplicamos una regla de tres inversa:
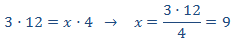
Se necesitan 9 personas.
Notemos que para pasar de la primera columna a la segunda multiplicamos por 3 en la primera fila y dividimos entre 3 en la segunda:
Problema 13
El precio de un barril de 100 litros de petróleo es de 65€. ¿Cuál es el precio de 3 barriles de 75 litros?
Ver solución
Se trata de una proporcionalidad directa: cuantos más litros, mayor es el precio del barril.
Llamamos x al precio de un barril de 75 litros:
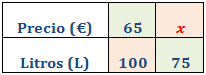
Como es una proporcionalidad directa, aplicamos una regla de tres directa:
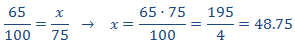
Como queremos tres barriles, multiplicamos por 3.
El precio total es de 3·48.75=146.25€
Problema 14
Completar la tabla para que las magnitudes de la primera fila sean inversamente proporcionales a las de la segunda e indicar cuál es la
constante de proporcionalidad.

Ver solución
Si multiplicamos la fila superior por la inferior tenemos:
En la columna 1:
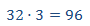
En la columna 2:
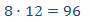
En la columna 4:
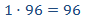
Por tanto, siempre que multiplicamos los números de una misma columna tenemos que obtener 96.
Completamos la tabla:
Llamamos x al hueco de la columna 3
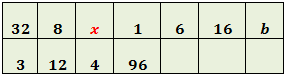
Tiene que cumplirse
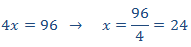
Para la columna 5:
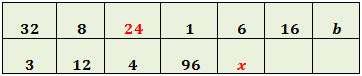
Tiene que cumplirse
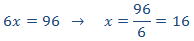
Para la columna 6:
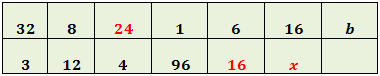
Tiene que cumplirse
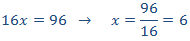
Para la columna 7:
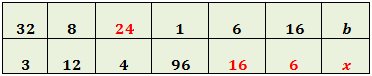
Tiene que cumplirse
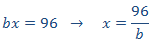
Por tanto, la tabla resultante es
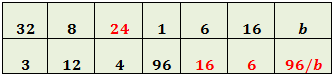
Nota: comparación de columnas:
Comparamos, por ejemplo, las columnas 2 y 6:

En la fila superior se multiplica por 2 y en la inferior se divide entre 2 (cuando una magnitud aumenta, la otra disminuye).

Problema 15
Cinco operarios tardan 9 horas en revisar el motor de todos los trenes de la estación. ¿Cuánto se tardaría en realizar el mismo trabajo si se contratan a dos operarios más?
Ver solución
Se trata de proporcionalidad inversa: cuantos más operarios, menor es el tiempo.
Llamamos x al número de horas.
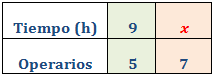
Como es una proporcionalidad inversa, aplicamos una regla de tres inversa:
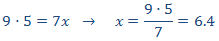
Se tardaría, aproximadamente, 6 horas y media.
Problema 16
Cuando abrimos la manguera el nivel del depósito de agua desciende 20cm cada 5 minutos. Calcular el tiempo que tarda en vaciarse el depósito si su nivel máximo es de 2.3m.
Ver solución
Se trata de una proporcionalidad directa: cuanto más tiempo está abierta la manguera, más baja el nivel del depósito.
Llamamos x al tiempo en minutos. Tengamos en cuenta que 2.3m son 230cm
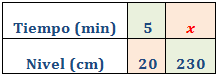
Como es una proporcionalidad directa, aplicamos una regla de tres directa:
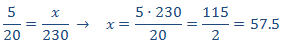
Es decir, el depósito tardará casi 1 hora en vaciarse.
Problema 17
Tres trabajadores recolectan 100 manzanos en 5 horas. Uno de ellos ha sufrido un accidente laboral y no puede continuar con su tarea. Calcular cuánto se tardará en recolectar los 300 manzanos restantes entre los dos trabajadores activos.
Ver solución
Problema de proporcionalidad inversa: cuantos más trabajadores, menos tiempo.
Llamamos x al tiempo:
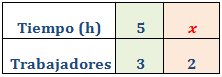
Como es una proporcionalidad inversa, aplicamos una regla de tres inversa:
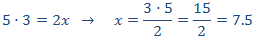
Tengamos en cuenta que este es el tiempo que tardarán en recolectar 100 manzanos. Como hay 300 manzanos, hay que multiplicar este tiempo por 3. Es decir, tardarán 22 horas y media.
Problema 18
Una empresa de refrescos dispone de 3 máquinas embotelladoras,
que son suficientes para satisfacer un pedido diario de 2400 botellas. En verano el pedido diario asciende a 5600 botellas. Calcular cuántas máquinas embotelladoras han de alquilarse para asumir el incremento de la demanda.
Ver solución
Proporcionalidad directa: cuanto más máquinas, más refrescos se embotellan.
Llamamos x al número de máquinas necesario para 5600 botellas:
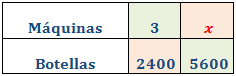
Como es una proporcionalidad directa, aplicamos una regla de tres directa:
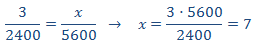
Se requieren 7 máquinas para embotellar 5600 refrescos. Como ya tenemos
3, hay que alquilar 7-3 = 4 máquinas.
Problema 19
Un camión realiza todos los días el mismo
recorrido entre dos almacenes. Se sabe
que tarda 3 horas y 20 minutos porque
mantiene una velocidad constante
de 90km/h. Mañana se debe entregar un paquete
urgente, pero el camión no puede
superar la velocidad máxima de 110km/h.
Se pide:
- Calcular el tiempo que tarda en realizar el envío a velocidad máxima.
- Calcular la distancia entre los almacenes.
Ver solución
a) Proporcionalidad inversa: cuanta más velocidad, menos tiempo.
Llamamos x al tiempo necesario.
Tengamos en cuenta que 3h y 20 minutos son

Como es una proporcionalidad inversa, aplicamos una regla de tres inversa:
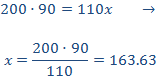
Como son muchos minutos, los pasamos a horas:
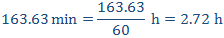
Y para expresarlo en horas y minutos:
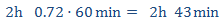
b) Tardamos 3h 20min a una velocidad de 90km/h.
Espacio recorrido es igual a velocidad por tiempo. Escribimos el tiempo en horas:
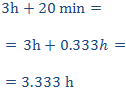
Por tanto, la distancia es de
$$ 3.333\cdot 90 \simeq 300\ km $$
Problema 20
Calcular el precio de una maleta de 130€ a la que se le aplicará una rebaja de un 60%.
Ver solución
El precio total de la maleta es el 100%.
Los porcentajes son relaciones de proporcionalidad
directa.
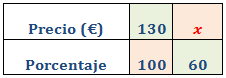
Como es una proporcionalidad directa, aplicamos una regla de tres directa:
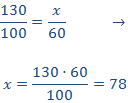
Es decir, el 60 por ciento son 78€. Como es el porcentaje de rebaja, el precio final será 130-78 = 52€.
Podemos hacer la regla de tres escribiendo 40 en vez de 60, que es el porcentaje que pagamos, y obtenemos directamente el precio final.

Nota: como se calculan habitualmente porcentajes, al dividir siempre entre 100 en la regla de tres, podemos multiplicar directamente la cantidad por (porcentaje a calcular)/100.
Por ejemplo, si queremos calcular el 60% de una cantidad, multiplicamos esta cantidad por 0.6. Si queremos calcular el 5%, multiplicamos por 0.05. Si queremos calcular el 125%, multiplicamos por 1.25.
Problema 21
En una tienda se aplica un mismo tanto por ciento de descuento en todos sus productos. Si pagamos 7€ por una camiseta que antes costaba 10€, ¿cuál era el precio inicial de unos pantalones que ahora cuestan 15€?
Ver solución
Proporcionalidad directa.
Usamos los precios de la camiseta para calcular el porcentaje:
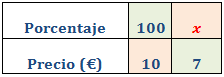
Como es una proporcionalidad directa, aplicamos una regla de tres directa:
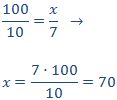
Es decir, hemos pagado un 70 por ciento del precio inicial (han rebajado un 30 por ciento).
Por tanto, también hemos pagado un 70% del precio inicial por los pantalones. Queremos calcular el 100%.
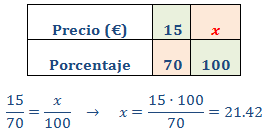
El precio inicial era 21.42€.


Proporcionalidad simple directa e inversa: regla de tres -
(c) -
matesfacil.com

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.