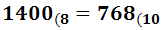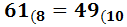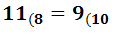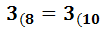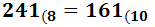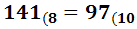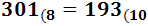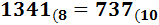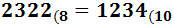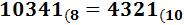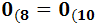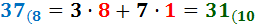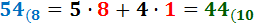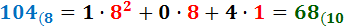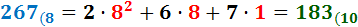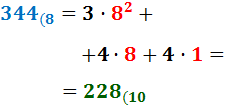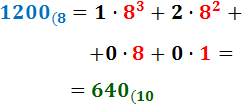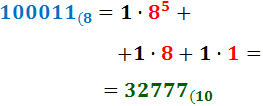Sistema de Numeración Octal
(Base 8)
Contenido de esta página:
-
Introducción
-
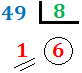
Cambio de base 10 a base 8 (método)
-
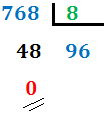
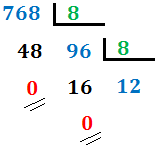
Cambio de base 8 a base 10 (método)
-
20 Ejercicios Resueltos: diez ejercicios de cambio de base 8 a base 10 y diez de cambio de base 10 a base 8
Introducción
El sistema decimal es un sistema de numeración posicional. Cuando nos enseñan los números por primera vez, éste es el sistema que se emplea y sin duda es el que más se usa en matemáticas. Sin embargo, hay otros sistemas de numeración que, debido a sus aplicaciones prácticas, también son importantes. Tal es el caso del sistema octal, que se utiliza a veces en informática.
El sistema octal es un sistema de numeración posicional de base 8.
Los símbolos que se usan en este sistema son:
0, 1, 2, 3, 4, 5, 6, 7
Para indicar que un número está escrito en base 8, usamos el subíndice \(_{(8}\), y para indicar que un número está escrito en base 10, usamos el subíndice \(_{(10}\).
Ejemplos:
-
\( 13_{(8} = 11_{(10} \)
-
\( 25_{(8} = 21_{(10} \)
-
\( 1077_{(8} = 575_{(10} \)
-
\( 7_{(8} = 7_{(10} \)
Observación:
El sistema octal sólo utiliza los dígitos del 0 al 7, con lo que los siguientes números NO están bien expresados:
-
\( 80_{(8} \)
-
\( 89_{(8} \)
-
\( 138_{(8} \)
-
\( 12A_{(8} \)
-
\( 2129_{(8} \)
Para pensar:
¿Puede haber un sistema posicional cuya base sea el número 1?
Hay un símbolo (0 en nuestro caso) que expresa la ausencia de unidades en un orden determinado.
¿Puede haber un sistema posicional sin un signo que indique esta ausencia?
Tenemos un número escrito en base 10. Si queremos pasarlo al sistema octal, ¿puede que necesitemos usar más cifras que en el sistema decimal?
Cambio de base decimal/octal
A continuación, explicamos cómo pasar un número del sistema decimal al sistema octal, y viceversa.
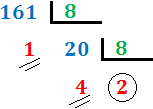
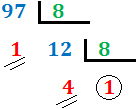
Cambio de base 10 a base 8
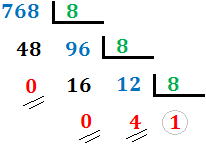
Cambio de base 8 a base 10

Ejercicios Resueltos de Cambio de Base
A. Cambio de base 10 a base 8
Escribir en base 8 los siguientes números escritos en el sistema decimal (es decir, en base 10):
Ejercicio 1: \( 49_{(10} \)
Ejercicio 2: \( 9_{(10} \)
Ejercicio 3: \( 3_{(10} \)
Ejercicio 4: \( 161_{(10} \)
Ejercicio 5: \( 97_{(10} \)
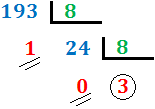
Ejercicio 6: \( 193_{(10} \)
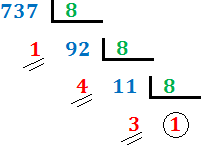
Ejercicio 7: \( 737_{(10} \)
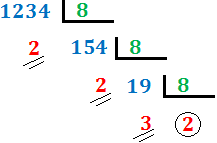
Ejercicio 8: \( 1234_{(10} \)
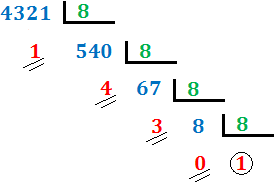
Ejercicio 9: \( 4321_{(10} \)
Ejercicio 10: \( 0_{(10} \)
B. Cambio de base 8 a base 10
Escribir en base 10 los siguientes números escritos en el sistema octal (es decir, en base 8):
Ejercicio 1: \( 37_{(8} \)
Ejercicio 2: \( 54_{(8} \)
Ejercicio 3: \( 104_{(8} \)
Ejercicio 4: \( 401_{(8} \)
Ejercicio 5: \( 156_{(8} \)
Ejercicio 6: \( 267_{(8} \)
Ejercicio 7: \( 344_{(8} \)
Ejercicio 8: \( 1200_{(8} \)
Ejercicio 9: \( 56754_{(8} \)
Ejercicio 10: \( 100011_{(8} \)
Sistema de numeración octal - (c) - matesfacil.com

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.