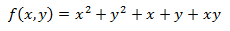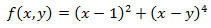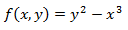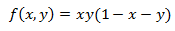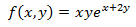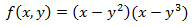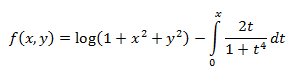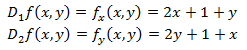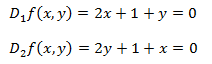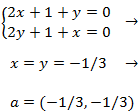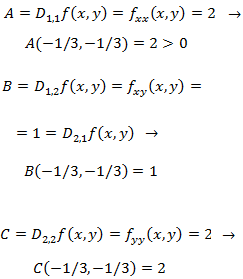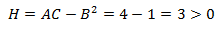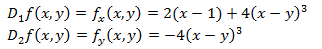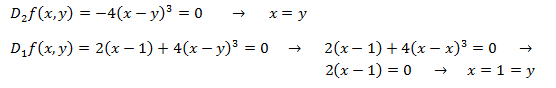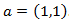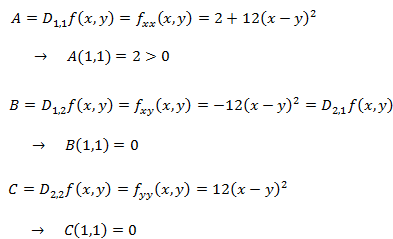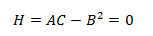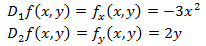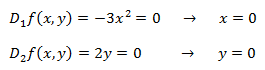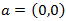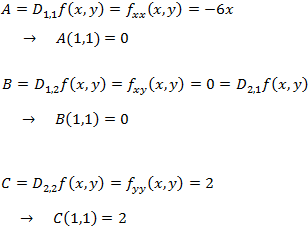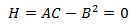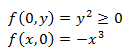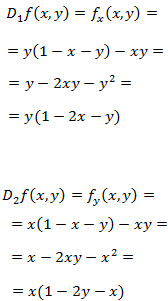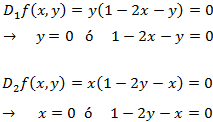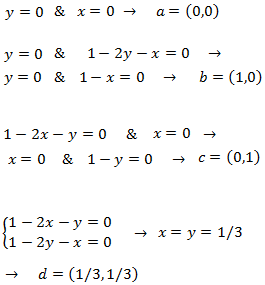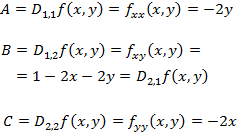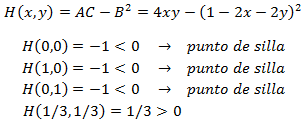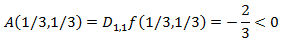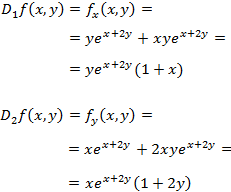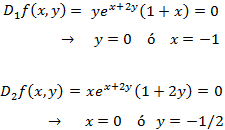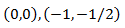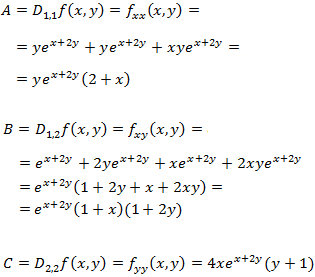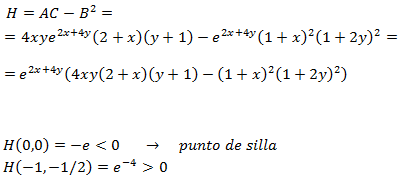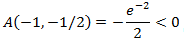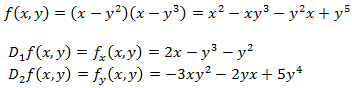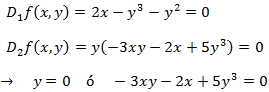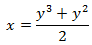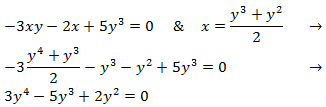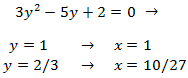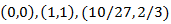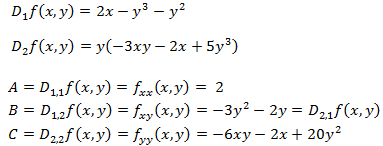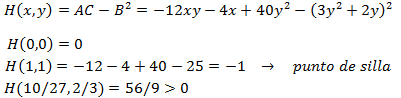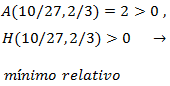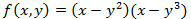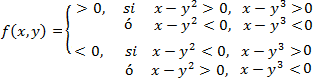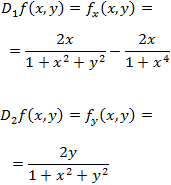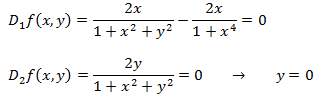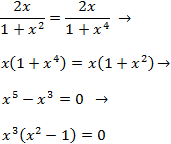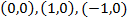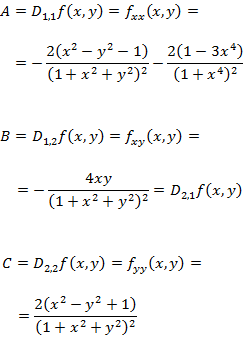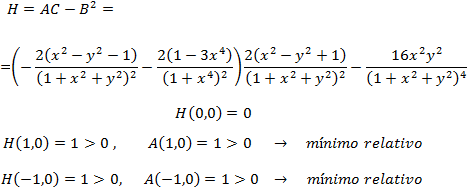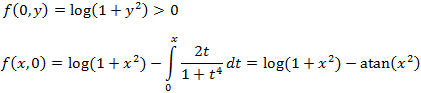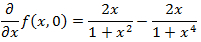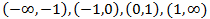Cálculo de Extremos de Funciones de Varias Variables |
Contenido de esta página:
-
Introducción
-
Método de Resolución: puntos críticos y de silla, condición suficiente de la existencia de extremos relativos y matriz Hessiana.
-
Ejercicios Resueltos: cálculo de extremos y de puntos de silla
Introducción
Al igual que las funciones de una variable, las de varias variables también
tienen extremos relativos y absolutos.
Un máximo (ó mínimo)
absoluto es un valor para el que la función toma el mayor (ó menor)
valor.
Un punto es un extremo relativo si es un extremo en un entorno de dicho punto. Es decir, si es un
extremo con respecto a los puntos cercanos.
En esta sección estudiaremos analíticamente la existencia de extremos
de funciones de dos variables en el dominio de la función (que consideramos
abierto). Para ello usaremos cálculo diferencial.
Método de Resolución
Nos basaremos, básicamente, en dos teoremas:
Puntos críticos: según teorema,
Si la función \(f\) admite derivadas
parciales (es decir, que existen) en un
extremo relativo \(a\), entonces son iguales a 0.
Es decir, los candidatos a extremos relativos son los puntos
que anulan las derivadas parciales. Es una condición
necesaria pero no suficiente, esto es,
que se anulen en \(a\) no significa que \(a\) sea un extremo, pero es un requisito indispensable.
A estos candidatos los llamamos puntos críticos.
Teorema: condición suficiente de extremos relativos:
Sean \(f\) una función de clase \(C^2\) en un abierto del plano que es entorno del punto \(a\), siendo \(a\) un punto crítico.
Llamamos a las derivadas parciales de \(f\) en \(a\) del siguiente modo:
$$ A = D_{1,1}f(a) $$
$$ B = D_{1,2}f(a) $$
$$ C = D_{2,2}f(a) $$
Y definimos el Hessiano de \(f\) en \(a\) como
$$ H = A\cdot C - B^2 $$
El Hessiano es el determinante de la matriz Hessiana.
Entonces se cumple que
-
Si \(H > 0\) y \(A<0\), entonces \(f\) tiene un máximo local en \(a\)
-
Si \(H > 0\) y \(A>0\), entonces \(f\) tiene un mínimo local en \(a\)
-
Si \(H < 0\), entonces \(f\) tiene un punto de silla en \(a\)
Un punto de silla es un punto donde el gradiente de la función es nulo. Es un punto donde la
superficie presenta un máximo con respecto a una dirección y un mínimo con respecto a la dirección perpendicular.
Ejercicios Resueltos
Ejercicio 1
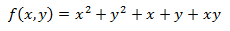
Ver Solución
Calculamos los puntos críticos
Calculamos las derivadas parciales de \(f\):
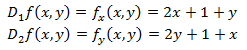
Los puntos críticos son aquellos que anulan a las derivadas parciales. Por tanto, igualamos a 0 las derivadas parciales para obtener un sistema de ecuaciones:
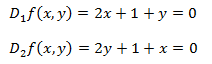
Resolvemos el sistema y obtenemos el punto crítico
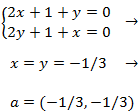
Calculamos el Hessiano y aplicamos el teorema
Evaluamos las derivadas parciales segundas en dicho punto:
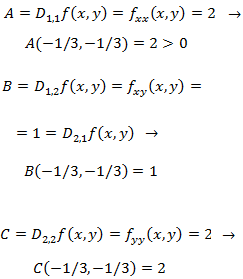
Por tanto, el Hessiano en dicho punto es
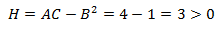
Con lo que, aplicando el teorema, el punto es un mínimo relativo.
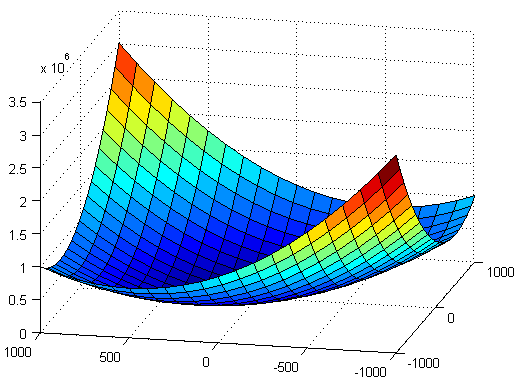
Ejercicio 2
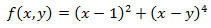
Ver Solución
Buscamos los puntos críticos
Las derivadas parciales son
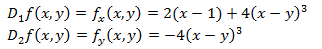
Los puntos críticos son aquellos que anulan a las derivadas parciales. Por tanto, queremos que
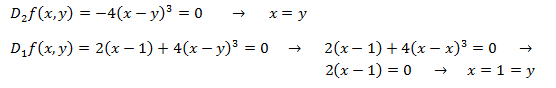
Tenemos un único punto crítico:
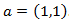
Aplicamos el teorema
Evaluamos las derivadas parciales segundas en dicho punto:
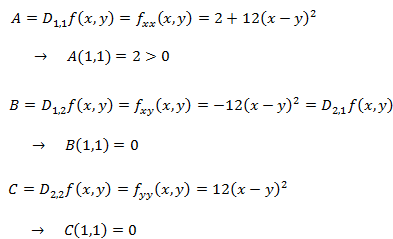
El Hessiano en dicho punto es
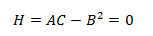
Y no podemos aplicar el teorema.
Notemos que la función nunca es negativa por ser la suma de potencias pares, por tanto, el punto crítico debe ser donde se anula la función y, por tanto, se trata de un mínimo absoluto.
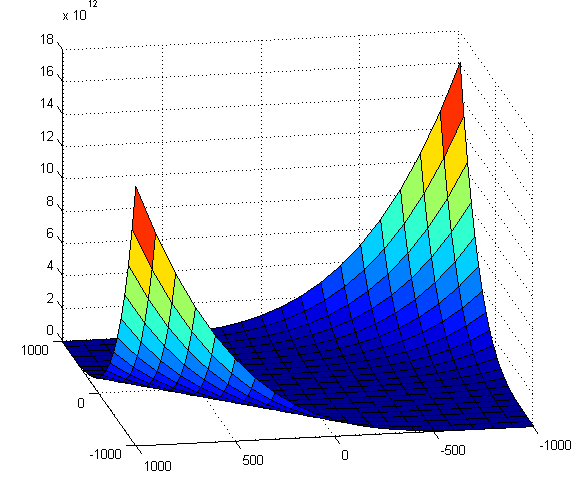
Ejercicio 3
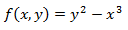
Ver Solución
Puntos críticos
Calculamos las derivadas parciales
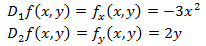
Las igualamos a 0:
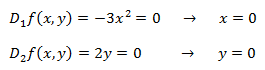
Tenemos un único punto crítico:
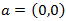
Aplicamos el Teorema
Evaluamos las derivadas parciales segundas en el punto crítico:
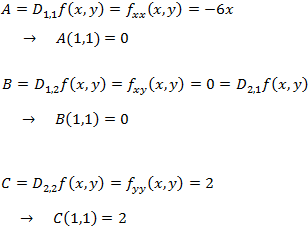
Por tanto, el Hessiano en el punto crítico es
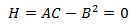
Y no podemos aplicar el teorema.
Puesto que la función se anula en el origen, estudiamos el signo de la
función en un entorno de éste, por ejemplo, en los ejes.
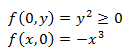
Desde el origen, la función crece sobre el eje OY y, sobre el eje OX, decrece hacia la derecha y crece hacia la izquierda. Por tanto, se trata de un punto de silla.
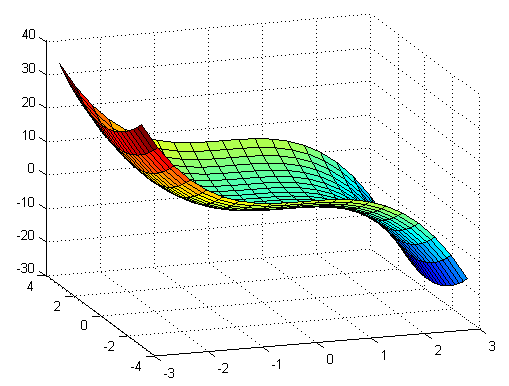
Ejercicio 4
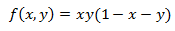
Ver Solución
Buscamos los puntos críticos
Las derivadas parciales son
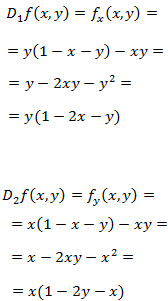
Los puntos críticos son aquellos que anulan a las derivadas parciales. Por tanto, queremos que
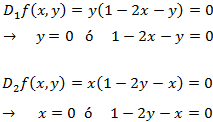
Tenemos cuatro puntos críticos:
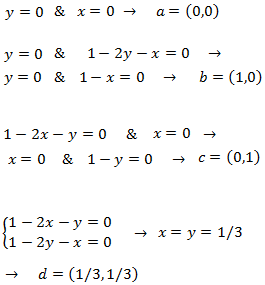
Las derivadas parciales segundas son
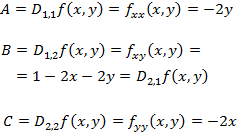
El Hessiano en cada punto es
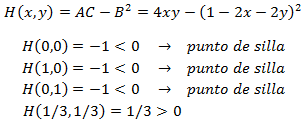
Para determinar el último punto crítico necesitamos saber el signo de
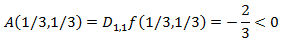
Por tanto, aplicando el teorema, se trata de un máximo relativo.
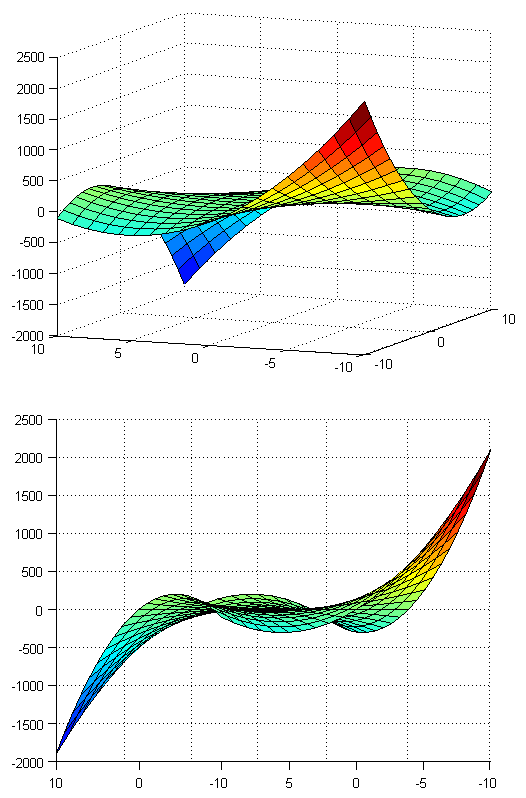
Ejercicio 5
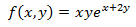
Ver Solución
Primero calculamos los puntos críticos.
Las derivadas parciales son
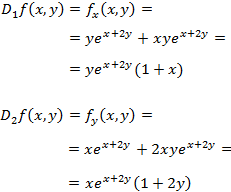
Los puntos críticos son aquellos que anulan a las derivadas parciales. Por tanto, queremos que
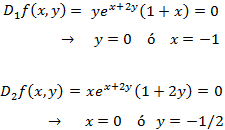
Puesto que han de cumplirse las dos ecuaciones, tenemos dos puntos críticos:
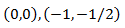
Las derivadas parciales segundas son
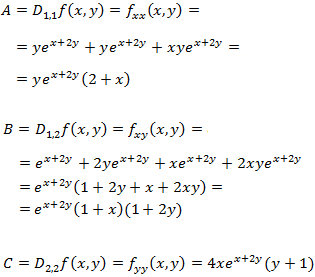
El Hessiano es
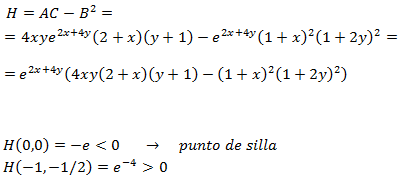
Necesitamos comprobar el signo de \(a\) para estudiar el segundo punto crítico:
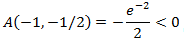
Por tanto, se trata de un máximo relativo.
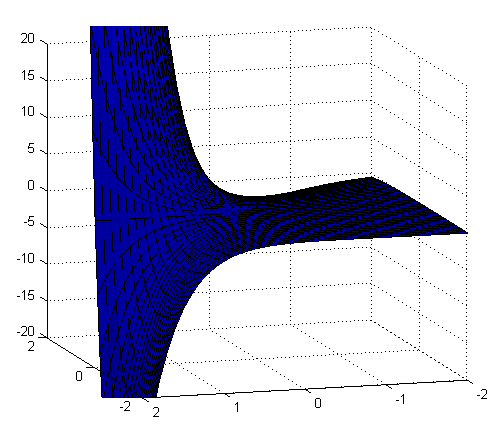
Ejercicio 6
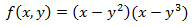
Ver Solución
Primero calculamos los puntos críticos.
Las derivadas parciales son
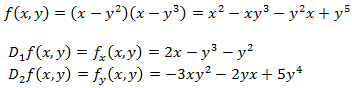
Los puntos críticos son aquellos que anulan a las derivadas parciales. Por tanto, queremos que
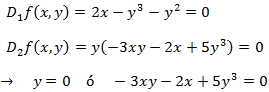
Supongamos que y = 0, con lo que se cumple la primera ecuación y, de la segunda, tenemos que
x = 0.
Asimismo, de la primera ecuación podemos despejar x:
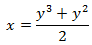
Sustituyendo en la segunda ecuación obtenemos
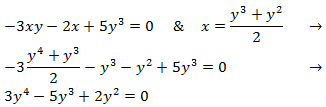
Hay dos soluciones que son y = 0, pero ya hemos contemplado este caso. Luego la ecuación queda
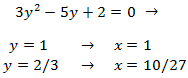
Hemos obtenido tres puntos críticos:
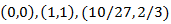
Derivadas parciales segundas:
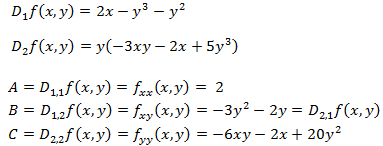
Por tanto, el Hessiano en los puntos críticos es:
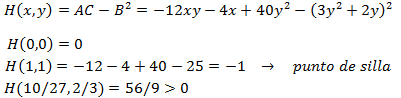
Analizamos el signo de A en el tercer punto crítico:
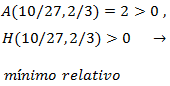
Falta estudiar el origen:
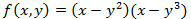
La función se anula en 0, por lo que tenemos que estudiar el signo de ésta en un entorno de dicho punto (método de las regiones).
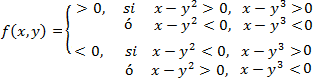
Representamos las distintas regiones:
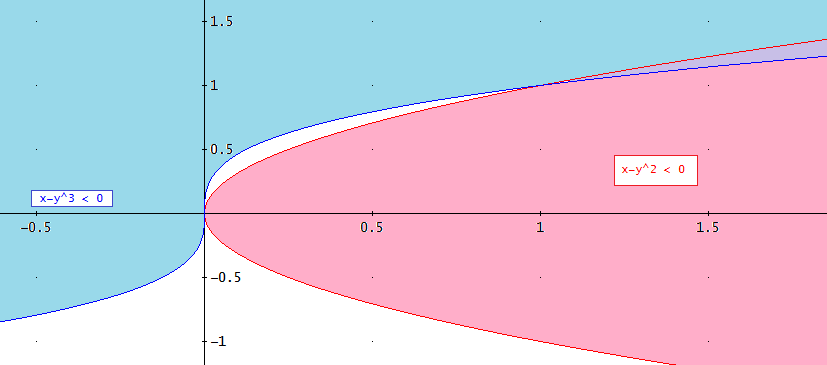
Ahora estudiamos el signo de la función en las distintas regiones:
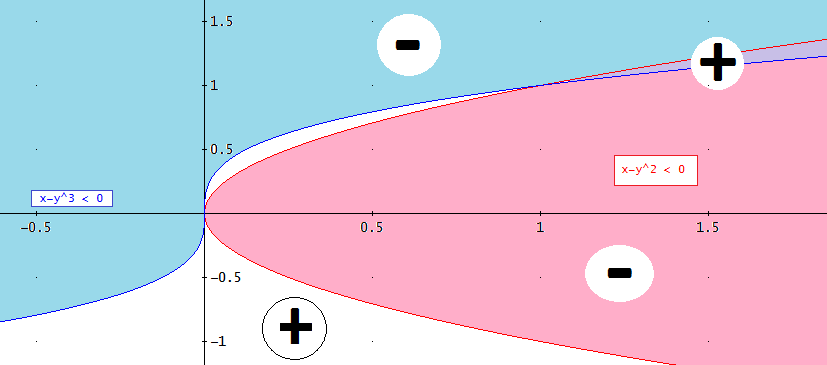
Tenemos signos positivos y negativos en cualquier entorno del origen, se trata, pues de un punto de silla.

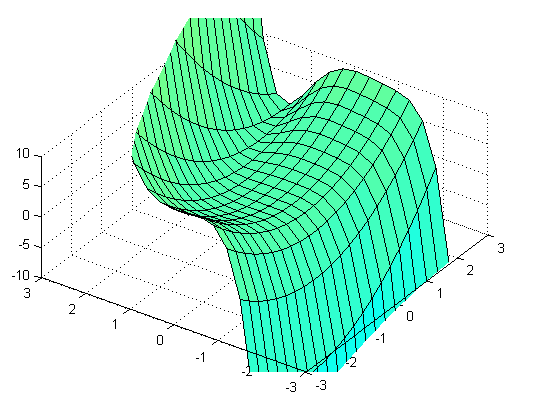
Ejercicio 7
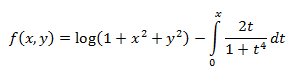
Ver Solución
Primero calculamos los puntos críticos.
Las derivadas parciales son
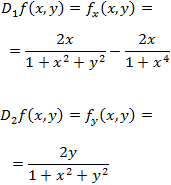
Los puntos críticos son aquellos que anulan a las derivadas parciales. Por tanto, queremos que
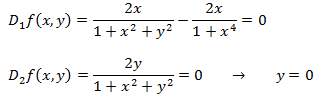
Como y = 0 , de la primera ecuación tenemos
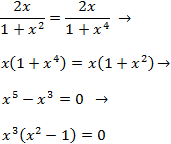
Luego tenemos los puntos críticos
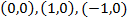
Las derivadas parciales segundas son:
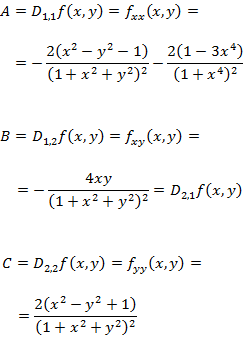
Por tanto, el Hessiano en dichos puntos es
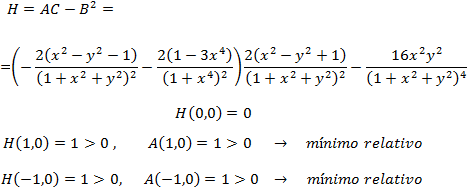
Falta el origen. Puesto la función se anula en dicho punto, estudiamos su signo en
un entorno, por ejemplo, sobre los ejes:
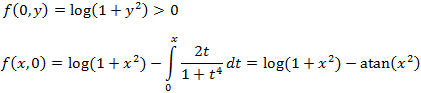
La función es positiva sobre el eje OY.
Estudiamos la monotonía de la función f(x,0)
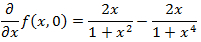
Sabemos que la derivada se anula en x = -1 , 0 , 1
Y tenemos que es decreciente, creciente, decreciente y creciente, respectivamente,
en los intervalos
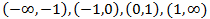
Al anularse en el origen y ser creciente y decreciente a su izquierda y a su derecha, respectivamente, deducimos que la función es negativa (en un entorno del origen) sobre el eje OX.
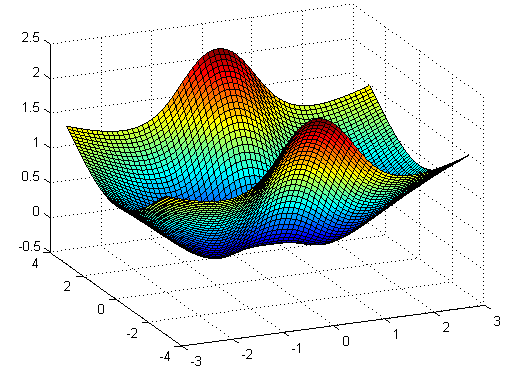
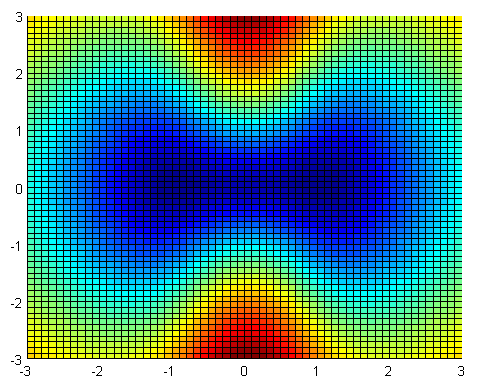
Con todo ello, concluimos que el origen es un punto de silla.


Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.