Autómata Finito Determinista |
Contenido de esta página:
Introducción.
-
Definición de Autómata Finito Determinista (AFD).
-
Representación de un AFD.
-
Lenguaje de un AFD.
-
Función de transición de estados extendida.
Páginas relacionadas:
-
Autómatas Finitos No deterministas y con transiciones-ε.
-
Ejemplos de Autómatas Finitos y Lenguajes Regulares.
-
Teoremas sobre los lenguajes de Autómatas.
-
Máquinas de Turing.
Introducción
La Teoría de Autómatas es una rama de la Teoría de la Computación que estudia las máquinas teóricas llamadas autómatas. Estas máquinas son modelos matemáticos.
Un Autómata está formado por un conjunto de estados, uno de los cuales es el estado en el que la máquina se encuentra inicialmente. Recibe como entrada una palabra (una concatenación de símbolos del alfabeto del autómata) y según esta palabra la máquina puede cambiar de estados.
Los Autómatas se clasifican según el número de estados (finito o no), la forma en que se realiza el cambio de estado (determinista o no), si acepta o no el símbolo vacío ε, si tiene o no una pila, etc.
Los Autómatas están estrechamente relacionados con la máquina de Turing (1936), de gran importancia en la Teoría de la Computación. Esto se debe a que una máquina de Turing puede simular el almacenamiento y la unidad de control de una computadora. Tenemos certeza de que lo que no puede ser resuelto por una máquina de Turing no puede ser resuelto por una computadora real.
Autómata Finito Determinista
Llamamos Autómata Finito Determinista a
$$ A = ( Q, \Sigma ,\delta , q_0 , F ) $$
siendo
Q el conjunto finito de estados, que denotaremos por
$$ q_0, q_1, q_2,...$$
Σ el alfabeto, es decir, un conjunto finito de símbolos que formarán palabras o cadenas.
El conjunto de palabras que se pueden formar concatenando los símbolos de Σ se denota por Σ*. La palabra vacía, que no está formada por ningún símbolo, forma parte de Σ*.
δ es la función de transición. Determina el comportamiento del autómata.
$$ \delta (q_i,a)=q_j $$
significa que si en el estado qi de Q el autómata recibe el símbolo de entrada a de Σ, entonces pasa al estado qj de Q.
q0 es el estado inicial, el estado en qué el autómata se encuentra inicialmente.
F es el subconjunto de Q (por tanto, finito) que contiene los estados de aceptación (o finales), que son los estados que provocan la parada del autómata.
Cuando se llega a uno de estos estados a través de una palabra w de Σ*, diremos que el autómata acepta a dicha palabra (es una palabra del lenguaje del autómata).
Representación o diagrama de un AFD
Representaremos los estados del AFD mediante círculos que encierran el nombre del estado (q0, q1,...).
La posible transición
$$ \delta (q_i,x)=q_j $$
se representa mediante una flecha que empieza en qi y termina en qj con la etiqueta "x".
Los circulos de los estados de aceptación tienen el borde doble.
El estado inicial, q0, se representa con una flecha que termina en dicho estado (pero no empieza en ningún estado).
EJEMPLO 1
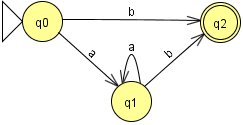
Lenguaje de un AFD
Llamamos lenguaje del autómata finito determinista A, L(A), al conjunto de palabras para las cuales el autómata llega a un estado de aceptación.
Si empleamos la función de transición extendida (definida más adelante), podemos definir el lenguaje como
$$ L(A):= \{ w\in {\Sigma}^* \ ∶\ \widehat{\delta} (q_0,w)\in F \} $$
EJEMPLO 2
Lenguaje del autómata del EJEMPLO 1.
Función de transición de estados extendida
Llamamos función de transición extendida a la función
$$ \widehat{\delta} $$
definida inductivamente como sigue:
$$ \widehat{\delta}(q_0, \epsilon)=q_0 $$
$$ \widehat{\delta}(q,w)= \delta( \widehat{\delta}(q,x),a) $$
siendo w una palabra que se puede descomponer como w = xa donde a es el último símbolo de la palabra w y x es la cadena de símbolos que precede a a.
PROBLEMA 3
Para el EJEMPLO 1
$$ \widehat{\delta} (q_0, aaab) = q_2 $$

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.
