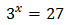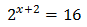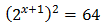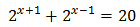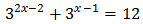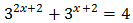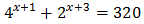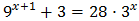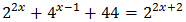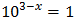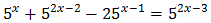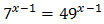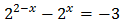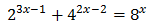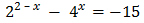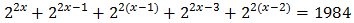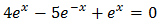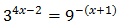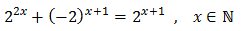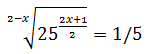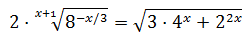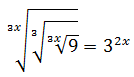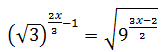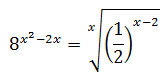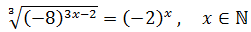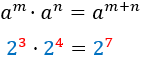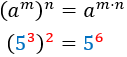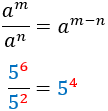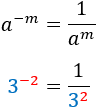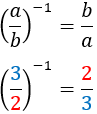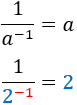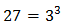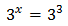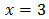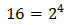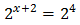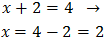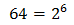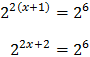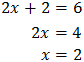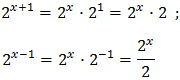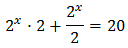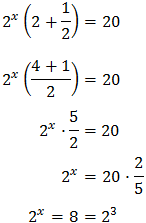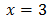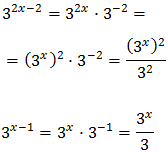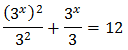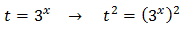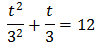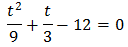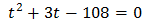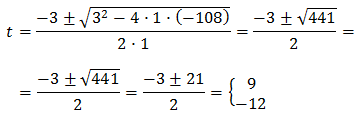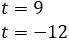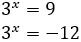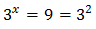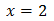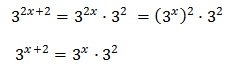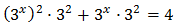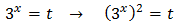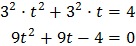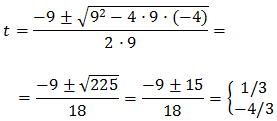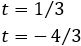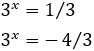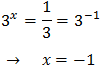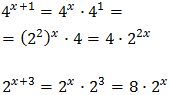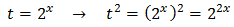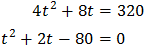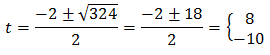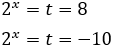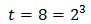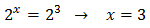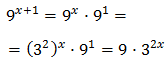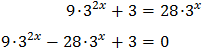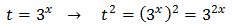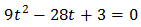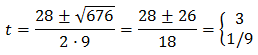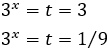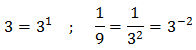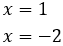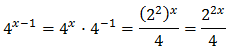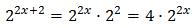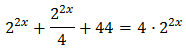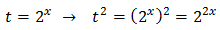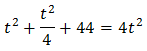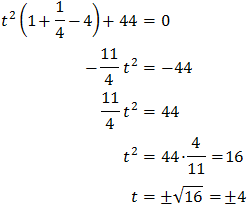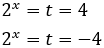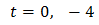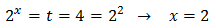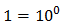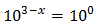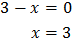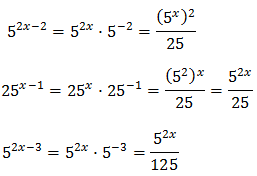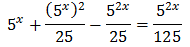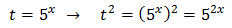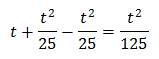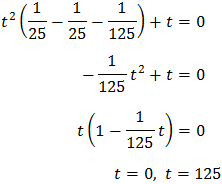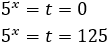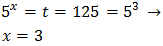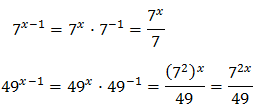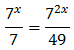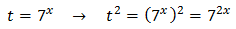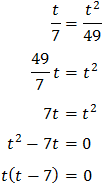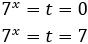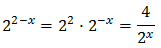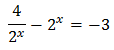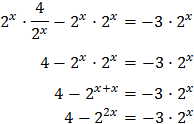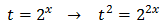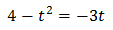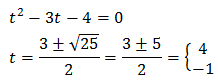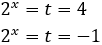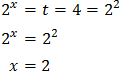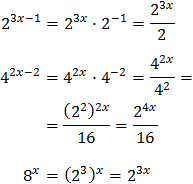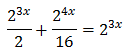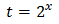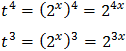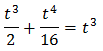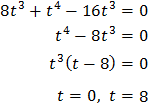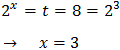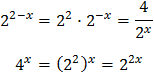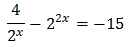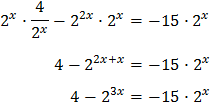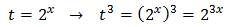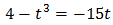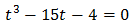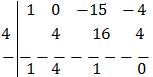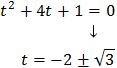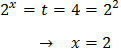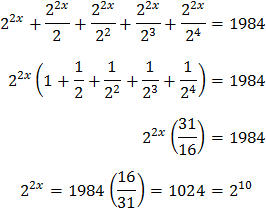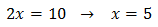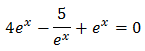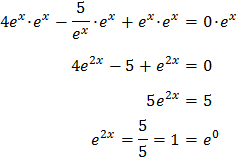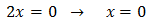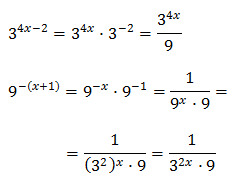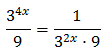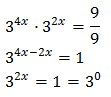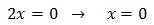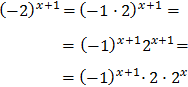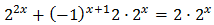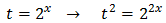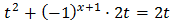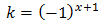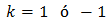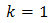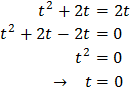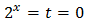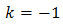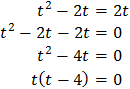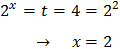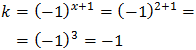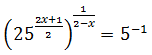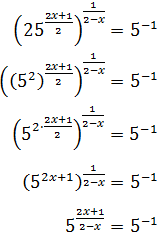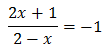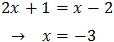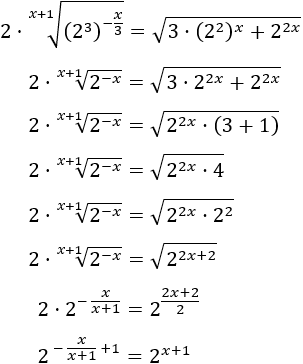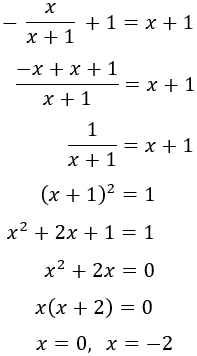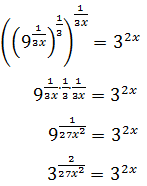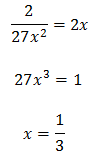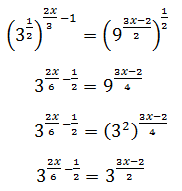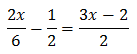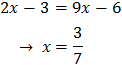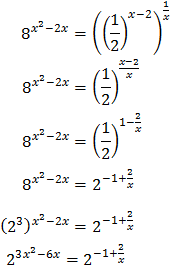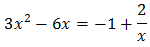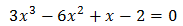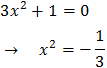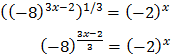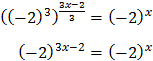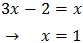Equacions Exponencials: Exercicis Resolts
Contingut d'aquesta pàgina:
Novetat!
Intel·ligència artificial
Com els algorismes condicionen les nostres vides
Enric Senabre, Vicent Costa
Més informació: sembra llibres.
|
 |
Introducció a les equacions exponencials
Una equació exponencial és aquella en la que apareixen exponencials, és a dir,
potències que tenen la incògnita, x, en els exponents. En aquesta pàgina resoldrem equacions
exponencials sense emprar logaritmes.
El mètode de resolució consisteix en aconseguir una igualtat entre dues exponencials amb la mateixa
base per poder igualar els seus exponents. Per exemple:
$$3^{2x}= 3^6$$
Òbviament, x ha de ser 3 perquè es compleixi la igualtat.
Per aconseguir aquest tipus de igualtats haurem de factoritzar, expressar els nombres
en forma de potències, aplicar les propietats de las potències
i escriure les arrels com potències. Sovint caldrà aplicar un canvi de variable
per transformar l'equació en una de segon grau.
Aquestes equacions també es poden resoldre, com hem dit abans, emprant logaritmes,
però nosaltres deixarem aquest procediment per a equacions més difícils en les que
les exponencials tenen bases distintes i, per tant, no podem igualar. Per exemple, l'equació
$$3^{x+3} = 5^x$$
té la solució real, emprant logaritmes,
$$x = 3 \frac{ln 3}{ln (\frac{5}{3})}$$
Abans de començar... recordem les propietats de les potències:
|
Producte (mateixa base)
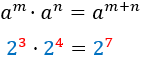
|
Potència (d'una potència)
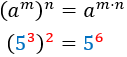
|
| Quocient
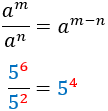
|
Exponent negatiu 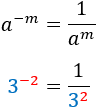
|
| Invers 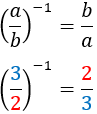
|
Invers
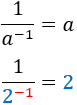
|
Equacions Exponencials Resoltes
Equació 1
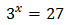
Veure solució
Tenim en compte que
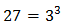
Podem reescriure l'equació com
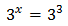
Per tant,
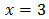
Equació 2
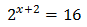
Veure solució
Tenim en compte que
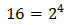
Podem reescriure l'equació com
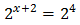
Per tant,
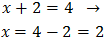
Equació 3
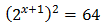
Veure solució
Tenim en compte que
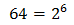
Operem en l'equació aplicant les propietats de les potències:
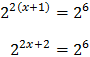
Per tant, tenim que
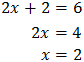
Equació 4
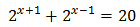
Veure solució
Tenim en compte que
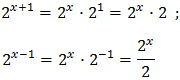
Així, podem reescriure l'equació com
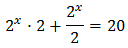
D'aquesta manera podem treure factor comú de \(2^x\)
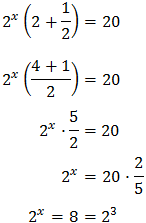
És a dir,
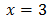
Equació 5
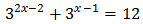
Veure solució
Tenim en compte que
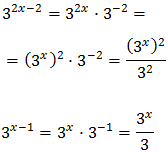
I d'aquesta manera podem reescriure l'equació com
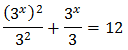
Tenim la base comú 3x però, com que una de les potències està al quadrat, escrivim
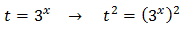
Substituint, l'equació queda com
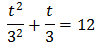
És a dir, una equació de segon grau
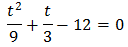
Multipliquem per 9:
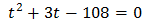
Resolem:
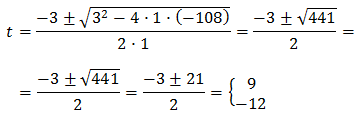
Per tant, tenim que
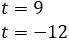
És a dir,
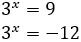
La segona opció no és possible perquè és negativa. Per tant,
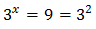
D'on obtenim
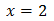
Equació 6
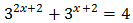
Veure solució
Tenim en compte que
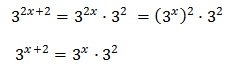
La qual cosa ens permet reescriure l'equació com
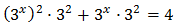
Anomenem
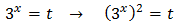
Substituïm i obtenim una equació de segon grau
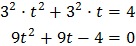
Resolem l'equació
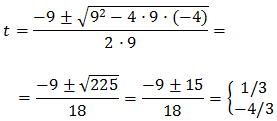
Per tant, tenim que
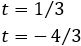
És a dir
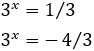
La segona solució no és possible per ser negativa, però la primera sí que ho és
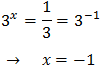
Equació 7
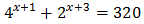
Veure solució
Tenim en compte que
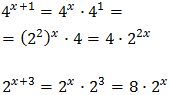
I així podem reescriure l'equació com

Anomenem
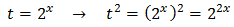
Substituïm i obtenim l'equació de segon grau
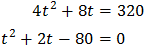
Resolem
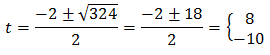
Tenim que
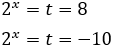
La segona solució no és possible per ser negativa. Per tant,
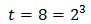
És a dir,
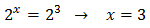
Equació 8
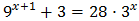
Veure solució
Tenim en compte que
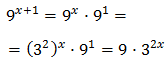
Així, podem reescriure l'equació com
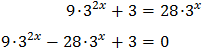
Anomenem
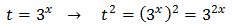
Substituïm i obtenim l'equació de segon grau
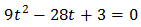
Resolem
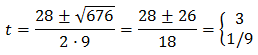
Per tant,
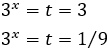
Notem que
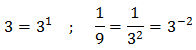
És a dir, ambdues són potències de 3. Llavors les solucions són
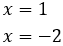
Equació 9
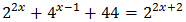
Veure solució
Tenim en compte que
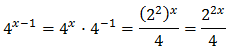
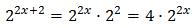
Així, podem reescriure l'equació com
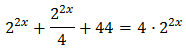
Anomenem
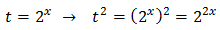
Substituïm i obtenim l'equació de segon grau
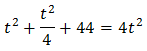
Resolem
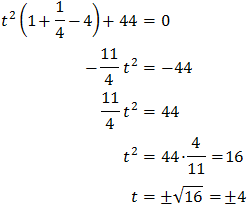
Per tant,
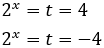
Las solucions
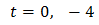
no són possibles per ser una zero i l'altra negativa. Llavors la solució de l'equació exponencial és
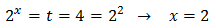
Equació 10
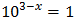
Veure solució
Tenim en compte que
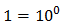
Així, podem reescriure l'equació com
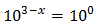
Per tant,
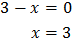
Equació 11
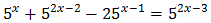
Veure solució
Tenim en compte que
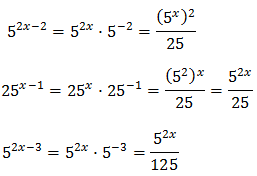
Així, podem reescriure l'equació com
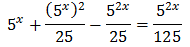
Anomenem
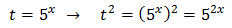
Substituïm i obtenim l'equació de segon grau
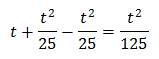
Resolem
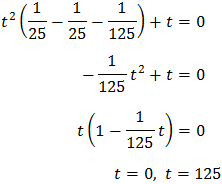
Per tant,
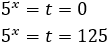
La primera no és possible per ser zero. Per tant,
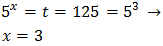
Equació 12
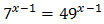
Veure solució
Tenim en compte que
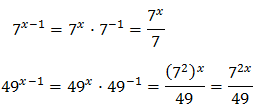
Així, podem reescriure l'equació com
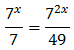
Anomenem
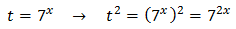
Substituïm i obtenim l'equació de segon grau
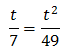
Resolem
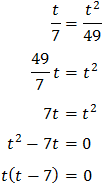
Per tant,
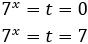
La primera no és possible per ser zero. Per tant, x = 1.
Equació 13
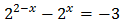
Veure solució
Tenim en compte que
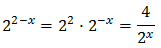
Així, podem reescriure l'equació com
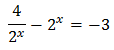
Com que tenim una exponencial dividint, multipliquem tota l'equació per aquesta perquè desaparegui:
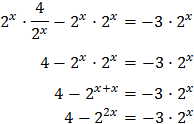
Anomenem
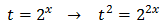
Substituïm i obtenim l'equació de segon grau
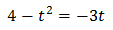
Resolem
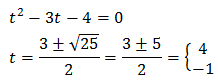
Per tant,
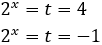
La segona no és possible per ser negativa. Per tant,
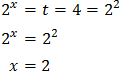
Equació 14
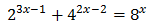
Veure solució
Tenim en compte que
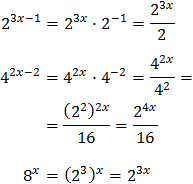
Així, podem reescriure l'equació com
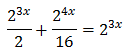
Anomenem
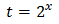
Aleshores
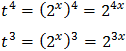
Substituïm i obtenim una equació de quart grau
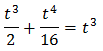
Resolem
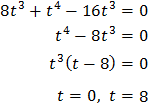
La primera solució no és possible per ser zero. Per tant,
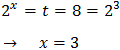
Equació 15
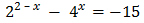
Veure solució
Tenim en compte que
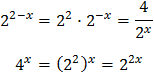
Així, podem reescriure l'equació com
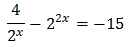
Com que tenim una exponencial dividint, multipliquem tota l'equació per aquesta perquè desaparegui:
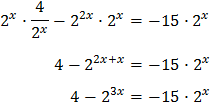
Anomenem
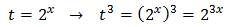
Substituïm i obtenim l'equació de tercer grau
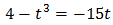
Resolem:
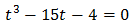
Apliquem la regla de Ruffini
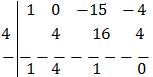
Una solució és t = 4. Calculem les altres dues:
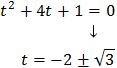
Però, aquestes no són solucions possibles ja que són negatives. Per tant,
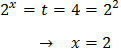
Equació 16
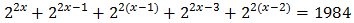
Veure solució
Reescrivim l'equació
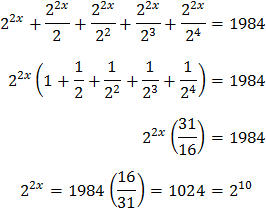
Per tant,
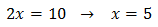
Equació 17
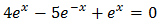
Veure solució
Reescrivim l'equació
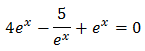
Com que tenim una exponencial en un denominador, multipliquem tota l'equació per aquesta perquè desaparegui:
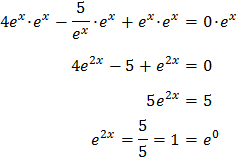
Per tant,
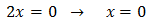
Equació 18
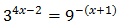
Veure solució
Tenim en compte que
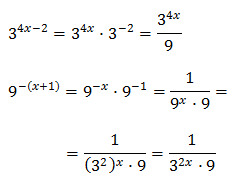
Reescrivim l'equació
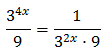
Operem:
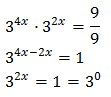
Per tant,
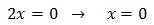
Equació 19: dificultat alta
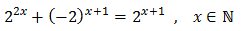
Veure solució
Tenim en compte que
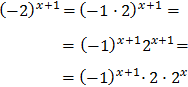
Així, podem reescriure l'equació com
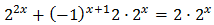
Anomenem
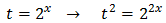
Obtenim l'expressió
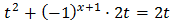
Anem a definir
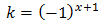
Notem que
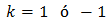
Anem a suposar primer que
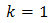
L'equació resultant és
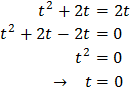
Així,
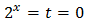
I açò no és possible. Suposem ara que
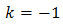
L'equació resultant és
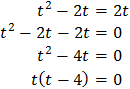
Una solució és t = 0 que, com abans, no és possible.
L'altra és
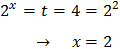
Però hem suposat que k = -1 i s'ha de comprovar que, en efecte, és així:
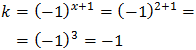
Com que la relació s'acompleix, la solució de l'equació exponencial és x = 2.
Equació 20
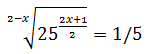
Veure solució
Podem reescriure l'equació com
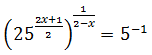
Anem a escriure 25 com 25 = 52 i, fent ús de les propietats de les potències, escrivim
l'arrel en forma de potència
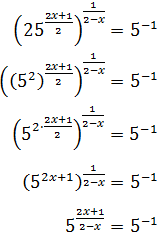
Per tant, tenim que
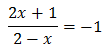
Finalment, resolem l'equació
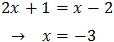
Equació 21
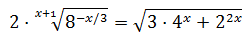
Veure solució
Escrivim les arrels en forma de potències
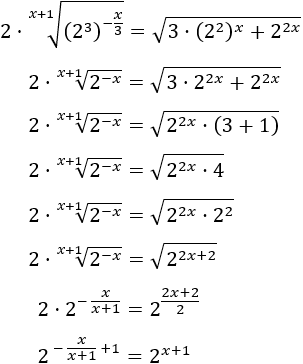
Volem que
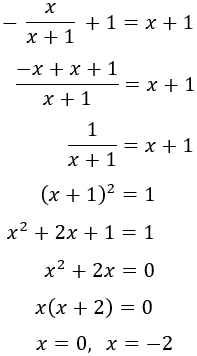
Per tant, tenim dues solucions:
$$x = 0, \ x = -2$$
Equació 22
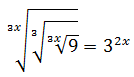
Veure solució
Escrivim les arrels en forma de potències
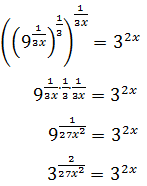
Volem que
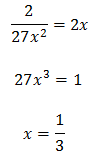
Equació 23
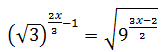
Veure solució
Escrivim les arrels en forma de potències. L'equació queda com:
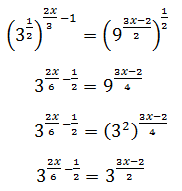
Volem que
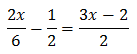
Resolem l'equació de primer grau i obtenim la solució:
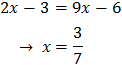
Equació 24
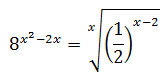
Veure solució
Escrivim l'arrel en forma de potència. L'equació queda com:
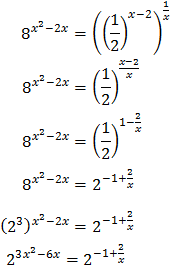
Volem que
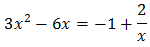
Hem de tenir en compte que x no pot ser mai 0 perquè està en el denominador.
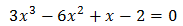
Resolem per Ruffini

Una arrel és x = 2. Calculem les altres:
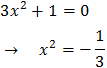
No hi ha arrels reals. Per tant, l'única solució de
l'equació exponencial és \(x = 2\).
Equació 25
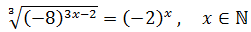
Veure solució
Escrivim l'arrel en forma de potència. L'equació queda com:
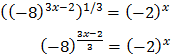
Notem que -8 = (-2)3
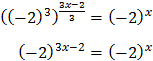
Volem que
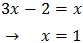

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.