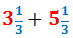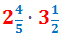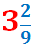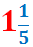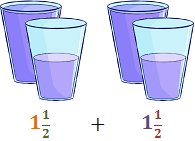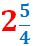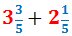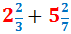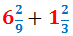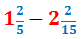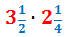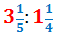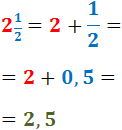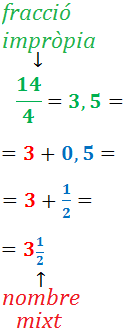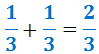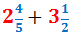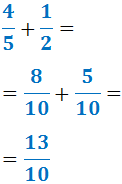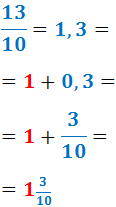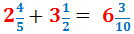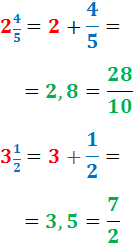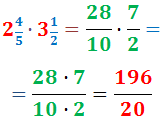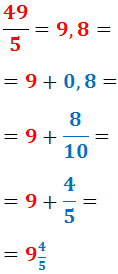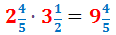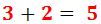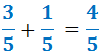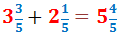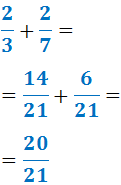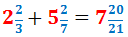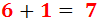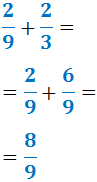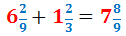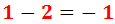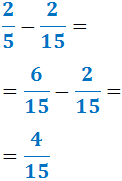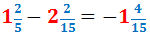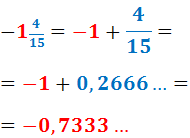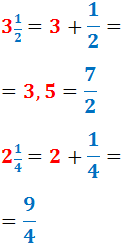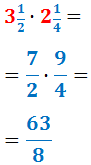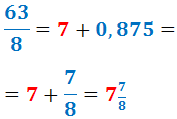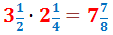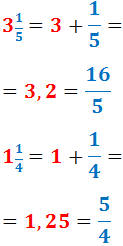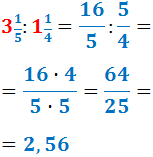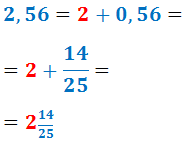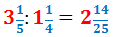Fraccions Mixtes: Test i Exercicis Resolts
|
Contingut d'aquesta pàgina:
-
Concepte de Fracció Mixta
-
De Fraccions Impròpies a Fraccions Mixtes
-
Operacions entre Fraccions Mixtes: suma, resta, producte i quocient
-
Test i Exercicis resolts: conceptes bàsics i operacions
Novetat!
Intel·ligència artificial
Com els algorismes condicionen les nostres vides
Enric Senabre, Vicent Costa
Més informació: sembra llibres.
|
 |
1. Concepte de Fracció Mixta

Veure Concepte
Els nombres mixtos (o fraccions mixtes)
són nombres formats per un nombre
enter (1,2,3,4,...) i una fracció pròpia
(el seu numerador és menor que el seu denominador).
El nombre enter de la fracció mixta és la seva part sencera i la fracció
pròpia és la part fraccionària o part decimal.
Exemple: fracció mixta dos i un mig

La part sencera és 2 i la fracció és ½.
La fracció és pròpia ja que el numerador, 1, és menor que el denominador, 2.
L'enter indica que hi ha 2 gots d'aigua "sencers" i la fracció indica que hi ha "mig got" d'aigua.
La fracció mixta representa el nombre que s'obté al sumar l'enter (part sencera) i la fracció pròpia
(part fraccionària).
Com que la fracció és pròpia (menor que 1), el resultat de la suma sempre és un nombre decimal.
Segons el que hem vist,
per passar d'un nombre mixt a un nombre
decimal
hem de sumar-li la fracció pròpia (en forma de decimals) a la part sencera.
Exemple:
En l'exemple anterior teníem dos gots i mig d'aigua:
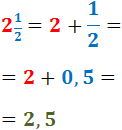
Les fraccions mixtes s'utilitzen, per exemple, en les receptes de
cuina i per expressar intervals de temps:
2. De Fraccions Impròpies a Fraccions Mixtes
(necessari per sumar nombres mixtos)
Veure Transformació
Les fraccions impròpies (numerador major o igual que el denominador)
són nombres majors (o iguales) que 1.
Per tant, ja que aquestes fraccions estan formades per al menys
una unitat, podem escriure-les com nombres mixtos: el nombre de unitats més els decimals.
Exemple:
La fracció catorze quarts és una fracció impròpia (ja que 14>4):
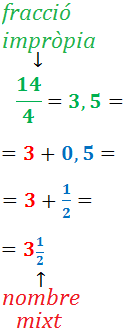
És a dir:
Escrivim la fracció com un nombre decimal.
-
Escrivim el nombre decimal com una suma: l'enter més la part fraccionària.
-
El segon sumand (el decimal) l'escrivim com una fracció
(pròpia).
Finalment, escrivim l'enter junt a la fracció.
3. Suma i Resta de Nombres Mixtos
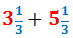
Veure Operacions
A l'hora de sumar (o restar) dos nombres mixtos tenim que sumar cadascuna de les seves parts:
les dues parts senceres i les dues fraccions.
A més, si al sumar les fraccions obtenim una fracció impròpia,
hem de reescriure el nombre mixt perquè la part fraccionària sigui una fracció pròpia.
És a dir:
Per sumar dues fraccions mixtes:
Sumem les parts senceres.
Sumem les parts decimals (les fraccions).
-
Comprovem que la fracció és pròpia, si no,
hem de sumar les seves unitats a la part sencera.
Exemple (cas fàcil):
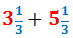
-
Sumem les parts senceres:

Sumem les fraccions:
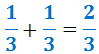
Com que la fracció resultant és pròpia, hem acabat.
La suma de les fraccions mixtes és:

Exemple (cas difícil):
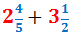
Sumem les parts senceres:

Sumem les fraccions: com que els denominadors són distints, hem d'utilitzar el
mínim comú múltiple de 5 i 2, que és 10:
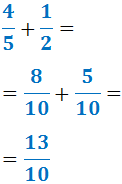
-
Com que la fracció resultant és impròpia (ja que 13 és major que 10),
hem de separar la part sencera:
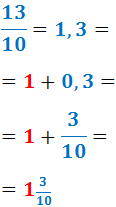
-
La part sencera d'aquest nombre mixt és
1 i l'hem de sumar a la part sencera
que hem calculat anteriorment:

Per tant, la suma de les fraccions mixtes és:
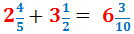
4. Producte de Nombres Mixtos
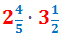
Veure Operació
La forma més rapida de multiplicar (o dividir)
fraccions mixtes és fer-ho en forma de fraccions (impròpies), és a dir,
Escrivim les fraccions mixtes com fraccions (impròpies) i les multipliquem.
Després, escrivim el resultat com una fracció mixta.
Exemple:
Anem a calcular el producte de nombres mixtos
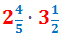
-
Escrivim les dues fraccions mixtes com fraccions impròpies:
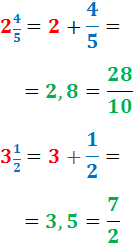
Multipliquem les fraccions (numerador per numerador i
denominador per denominador):
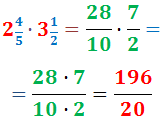
Simplifiquem el resultat (dividim el numerador i el denominador entre 4):
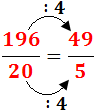
-
La fracció anterior és impròpia, així que anem a separar
la part sencera i la decimal:
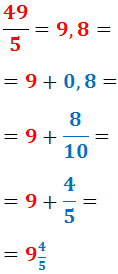
Nota: hem simplificat la fracció 8/10 dividint entre 2.
-
Per tant, el producte de les fraccions mixtes és
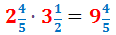
Test i Exercicis Bàsics de Fraccions Mixtes
Exercici 1
Considerar la fracció mixta
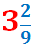
Triar l'opció correcta:
|
|
La part sencera de la fracció mixta es 3
i la part fraccionària és 2/9.
|
|
|
La part sencera de la fracció mixta es 2/9 i la part fraccionària és 3.
|
Exercici 2
El nombre mixt
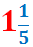
és el nombre decimal...
Exercici 3
Considerar el següent nombre mixt:

Triar l'afirmació correcta:
|
|
És el nombre 5 ja que els dos 7’s poden simplificar-se.
|
|
|
És la fracció mixta set i cinc setens.
|
|
|
No és correcte escriure aquest nombre mixt ja que el denominador és major que el numerador.
|
Exercici 4
El nombre decimal 5,75 pot escriure's com la fracció mixta...
|
|
5¼
|
|
|
5¾
|
|
|
Ninguna de les anteriors.
|
Exercici 5

El nombre de gots d'aigua és...
|
|
2½
|
|
|
3½
|
|
|
Ninguna de les anteriors.
|
Exercici 6
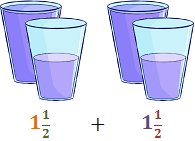
El resultat de la suma de les fraccions mixtes és...
Exercici 7
Considerar el nombre mixt
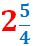
Quina de les següents afirmacions és FALSA?
|
|
No és completament correcte escriure aquest nombre mixt ja que la fracció és impròpia.
|
|
|
És el doble de cinc quarts.
|
|
|
És preferible escriure el nombre mixt 3¼.
|
Exercici 8
Si al exprimir 3 taronges tenim 2 gots de suc,
quantes taronges són necessàries per a tenir un got de suc?
Exercici 9
Calcular la següent suma de fraccions mixtes:
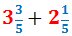
Veure Solució
Sumem les parts senceres:
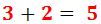
Sumem les parts decimals:
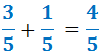
Per tant, la suma és
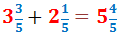
Exercici 10
Calcular la següent suma de fraccions mixtes:
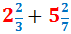
Veure Solució
Sumem les parts senceres:

Sumem les parts decimals (no oblidem que els denominadors són distints):
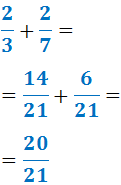
Com que la fracció és pròpia
(denominador major que numerador),
ja podem escriure el nombre mixt:
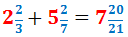
Exercici 11
Calcular la següent suma de nombres mixtos:
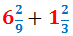
Veure Solució
Sumem les parts senceres:
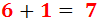
Sumem les parts decimals (les fraccions):
Com que els denominadors són distints, necessitarem el mínim comú múltiple de 9 i de 3, que
és 9.
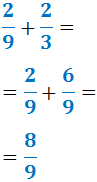
La fracció obtinguda és pròpia, per tant, ja podem escriure el nombre mixt:
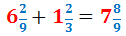
Exercici 12
Calcular la següent resta de fraccions mixtes:
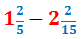
Veure Solució
La resta es calcula de manera similar a la suma.
Restem les parts senceres:
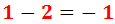
Nota:
recordem que la suma de dos nombres de
signe distint es calcula restant els nombres i
mantenint el signe del major.
Restem les fraccions:
El mínim comú múltiple de 5 i 15 és 15.
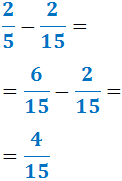
Com que la fracció és pròpia, ja podem escriure el nombre mixt:
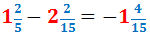
Nota: la fracció mixta obtinguda és el nombre decimal:
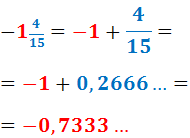
Exercici 13
Calcular el següent producte de fraccions mixtes:
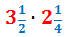
Veure Solució
Escrivim les dues fraccions mixtes com fraccions impròpies (sumant la part sencera i la fracció):
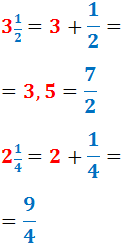
Nota: per obtenir les fraccions impròpies hem calculat les sumes:
$$ 3 + \frac{1}{2} = $$
$$ = \frac{6}{2} + \frac{1}{2} = \frac{7}{2} $$
$$ 2 + \frac{1}{4} = $$
$$ = \frac{8}{4} + \frac{1}{4} = \frac{9}{4} $$
Multipliquem les fraccions (numerador per numerador i denominador per denominador):
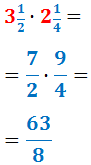
La fracció obtinguda és impròpia, així que la escrivim com una fracció mixta:
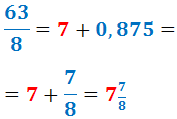
Per tant, el producte de les fraccions impròpies és:
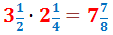
Exercici 14
Calcular la següent divisió de fraccions mixtes:
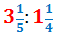
Veure Solució
Farem el mateix que quan calculem el producte però, dividint les fraccions impròpies en
lloc de multiplicar-les.
Escrivim les fraccions mixtes com fraccions impròpies:
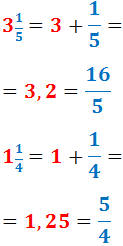
Dividim les dues fraccions obtingudes (multipliquem en creu: numerador per denominador i
denominador per numerador):
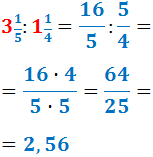
Escrivim el nombre decimal obtingut com un nombre mixt:
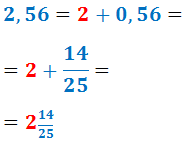
Per tant,
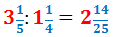

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.