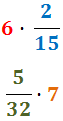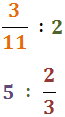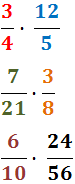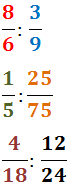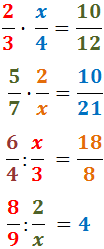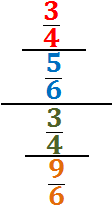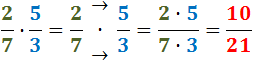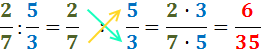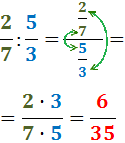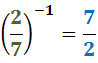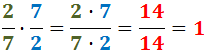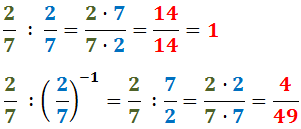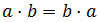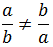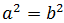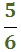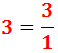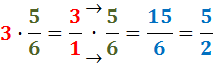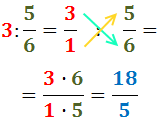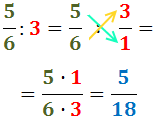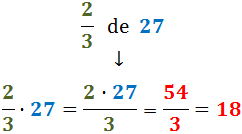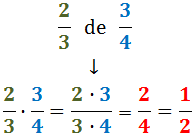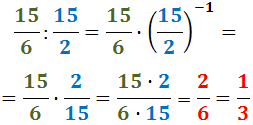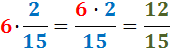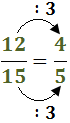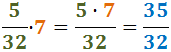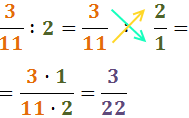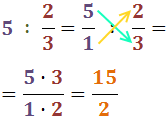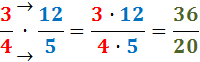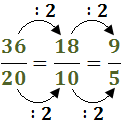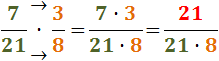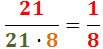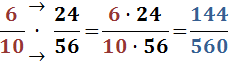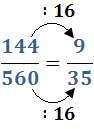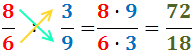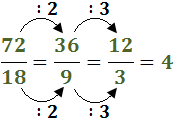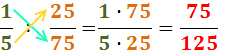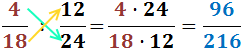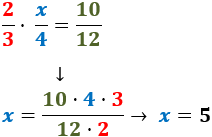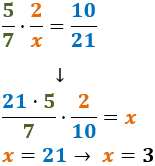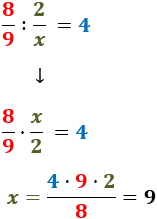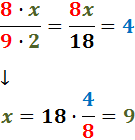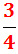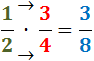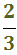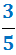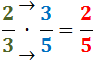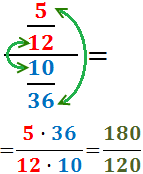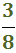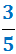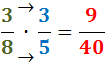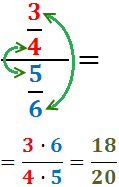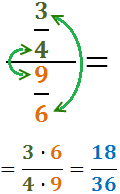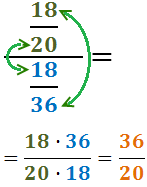Multiplicar i Dividir Fraccions: Exercicis Resolts
|
Contingut d'aquesta pàgina:
Novetat!
Intel·ligència artificial
Com els algorismes condicionen les nostres vides
Enric Senabre, Vicent Costa
Més informació: sembra llibres.
|
 |
Introducció
Com ja sabem, les fraccions representen nombres. Per tant, és lògic que els puguem sumar, restar,
multiplicar i dividir al igual que ho fem amb
els nombres enters o els decimals.
En aquesta pàgina anem a veure com multiplicar i
dividir fraccions. A diferència de la suma (o resta),
aquestes operacions no requereixen que els denominadors siguin iguals.
Finalment, com es d'esperar, el resultat d'aquestes operacions és
una fracció, encara que és recomanable escriure la seva forma irreductible
(fracció simplificada al màxim), per la qual cosa el resultat pot ser
un nombre enter (per exemple, al reduir la fracció 4/2 obtenim l'enter 2).
Multiplicació de Fraccions
Veure Operació
El resultat del producte de dues fraccions és la fracció que:
Exemple (el punt · representa l'operació
multiplicació):
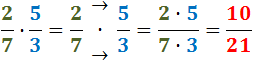
En aquest exemple el resultat ja és irreductible.
Com a regla mnemotècnica solen escriure's les fletxes Paral·leles
(Producte) per indicar que els nombres deuen multiplicar-se; per
al Quocient (divisió) s'utilitzen les fletxes Creuades.
Divisió de Fraccions
Veure Operació
La divisió de dues fraccions és la fracció que:
Exemple (els dos punts : representen la divisió):
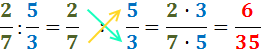
Notes i Consells
Veure Consells
-
Regla mnemotècnica: el Producte
es calcula multiplicant en Paral·lel i el
Quocient (divisió) se
calcula multiplicant en Creu.
-
La divisió pot representar-se com un quocient de fraccions. Per exemple,
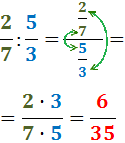
Regla mnemotècnica: en el numerador
multipliquem el de dalt, el 2, pel de baix, el 7;
i en el denominador multipliquem els dos del mig, 7 i 5.
Producte per l'invers: el producte d'una fracció pel seu invers
(canviem numerador per denominador) és 1.
Exemple:
El invers de 2/7 es
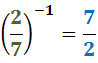
Aleshores,
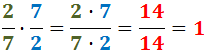
Nota: no ocorre el mateix amb la divisió. Si dividim la fracció per
ella mateixa, obtenim 1; però no si la dividim pel seu invers (obtenim el seu quadrat):
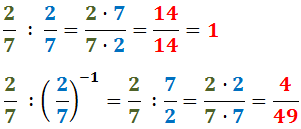
El producte és commutatiu:
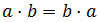
Però la divisió NO és commutativa:
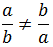
Excepte el cas que
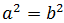
Producte i Divisió d'una Fracció per un Enter
Veure Operació
Si volem calcular el producte o la divisió d'una
fracció per un enter, podem escriure l'enter com
una fracció (escrivint el denominador 1) i aplicar les regles que hem vist.
Exemple: considerem l'enter 3 i la fracció
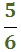
Podem escriure l'enter com
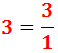
El seu producte és:
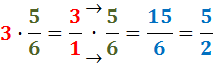
Les divisions són:
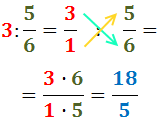
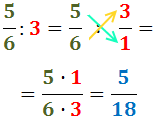
Nota: el producte (o divisió) d'una fracció
per un real es calcula de la mateixa manera.
Interpretació del Producte de Fraccions
Veure Text
Habitualment, ens trobem amb problemes (d'aplicació de les fraccions) en els
que hem de calcular sumes i restes de fraccions, o bé, fraccions d'una
certa quantitat.
Recordem que quan volem calcular
la fracció d'una quantitat multipliquem la fracció per dita quantitat.
Per exemple, dos terços de 27 són
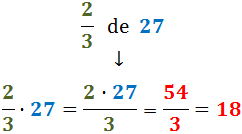
Encara que sembla estrany, sovint la quantitat de la qual
volem conèixer la seva fracció és també una fracció
(veure exercici 9). Aleshores, hem de calcular el producte de les dues fraccions.
Per exemple, dos terços de tres quarts són:
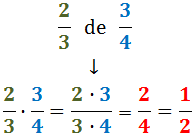
(en l'última igualtat hem reduït la fracció)
La Divisió escrita com un Producte
Veure Explicació
Ja que dividir és el mateix que multiplicar per l'invers,
podem transformar les divisions de fraccions
en productes de fraccions.
Açò s'aconsegueix multiplicant per l'invers de la fracció que divideix.
Exemple:
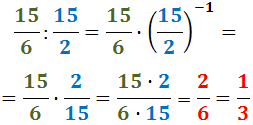
(en l'última igualtat hem reduït la fracció)
Exercicis Resolts
Exercici 1
Calcular els següents productes d'un enter per una fracció:
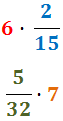
Veure solució
El producte es calcula multiplicant l'enter al numerador:
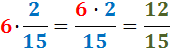
Simplifiquem el resultat:
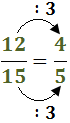
El segon producte és:
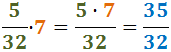
No podem simplificar el resultat ja que la fracció ja és irreductible.
Exercici 2
Calcular les següents divisions d'una fracció i un enter:
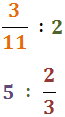
Veure solució
Per facilitar els càlculs escriurem els enters com fraccions.
Açò ho podem fer, per exemple, afegint el denominador 1.
Recordem que la divisió es calcula multiplicant en creu:
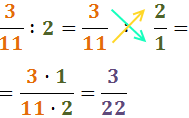
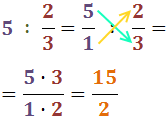
Els resultats ja són fraccions irreductibles.
Exercici 3
Calcular els següents productes de fraccions:
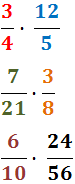
Veure solució
Recordem que el producte de fraccions es
calcula multiplicant els numeradors i
els denominadors en paral·lel.
El primer producte és
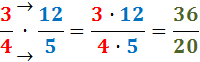
Reduïm la fracció:
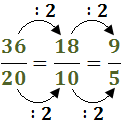
El segon producte és
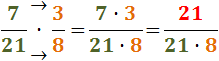
No hem calculat el producte del denominador perquè així és més
ràpid simplificar (tenim 21 en el numerador i en el denominador):
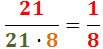
El tercer producte és
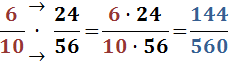
Reduïm la fracció:
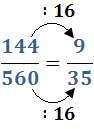
Nota: hem dividit per 16 directament. Açò és el mateix que
dividir per 2 quatre vegades.
Exercici 4
Calcular les següents divisions de fraccions:
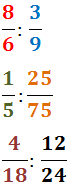
Veure solució
Recordem que la divisió de fraccions es
calcula multiplicant numeradors i denominadors en creu:
La primera divisió es
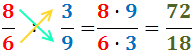
Reduïm la fracció:
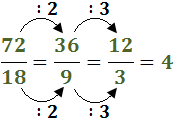
La segona divisió es
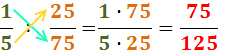
Simplifiquem:
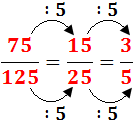
La tercera divisió es
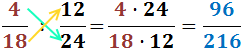
Reduïm:
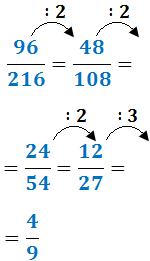
Exercici 5
Calcular x perquè es compleixin les igualtats:
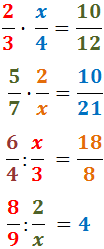
Veure solució
En la primera igualtat, com que tenim un
producte de fraccions, és molt senzill obtenir
el valor de x ja que multipliquem
els numeradors i els denominadors en paral·lel:
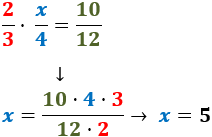
Segona igualtat: de manera similar,
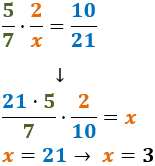
En les divisions, el procés és un poc més complicat
ja que els productes es calculen en creu:
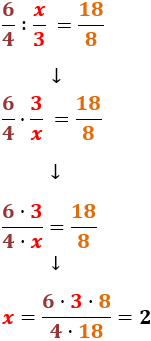
Finalment,
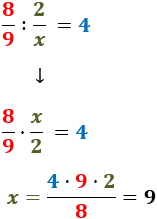
Calcular x no és tan
directe perquè al costat dret no hi ha denominador.
Hem d'aïllar la incògnita:
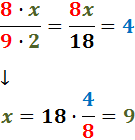
Exercici 6
Quina fracció del total és la meitat d'una tercera quarta part?
Veure solució
Una tercera quarta part s'obté al multiplicar per
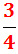
La meitat sempre s'obté multiplicant per
un mig.
Per tant, la meitat d'una tercera quarta part és
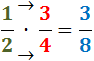
Exercici 7
Calcular quant són dos terços de tres cinquenes parts.
Veure solució
Dos terços són
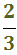
i tres cinquens són
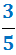
Llavors dos terços de tres cinquens són
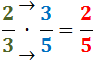
Exercici 8
Calcular la divisió de fraccions
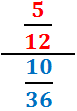
Veure solució
Las fletxes indiquen els productes que realitzem:
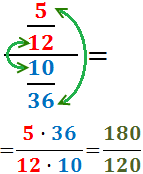
Simplifiquem el resultat:
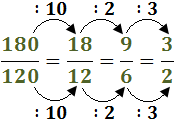
Exercici 9
Utilitzem tres cinquenes parts de l'aigua d'un dipòsit que només conté tres vuitenes
parts de la seva capacitat total.
Calcular la fracció d'aigua que hem utilitzat respecte a la capacitat total del dipòsit.
Veure solució
El dipòsit conté tres vuitenes parts, que és la fracció:
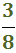
Consumim tres cinquenes parts, que és la fracció:
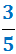
Llavors tres cinquenes parts de tres vuitenes parts és el producte
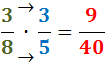
Exercici 10
Calcular el següent quocient de quocients:
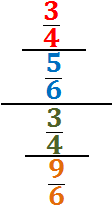
Veure solució
Tenim una divisió de fraccions en el
numerador i altra en el denominador.
Anem a calcular primer aquestes dues divisions i, després, a dividir els resultats.
La divisió del numerador és:
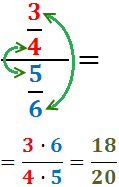
La divisió del denominador és:
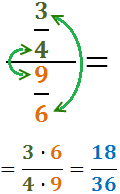
La divisió dels resultats anteriors és:
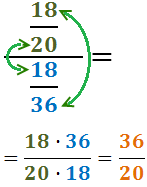
Finalment, simplifiquem el resultat:


Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.