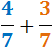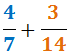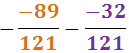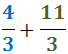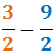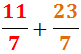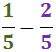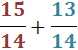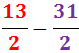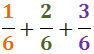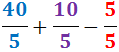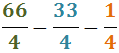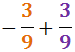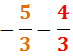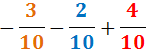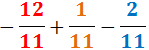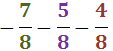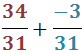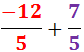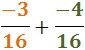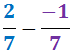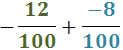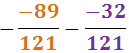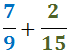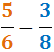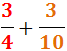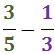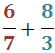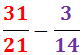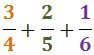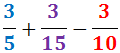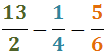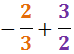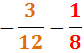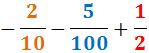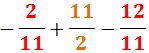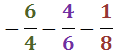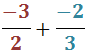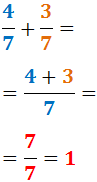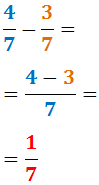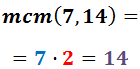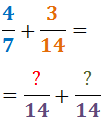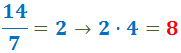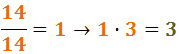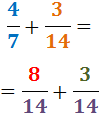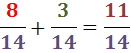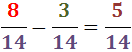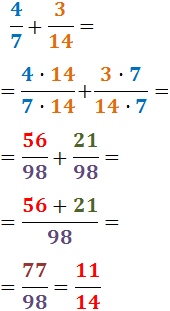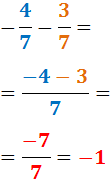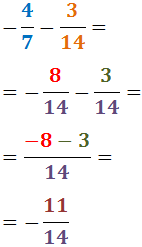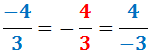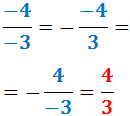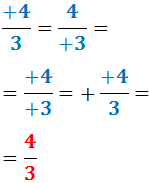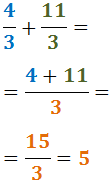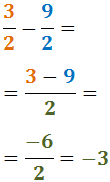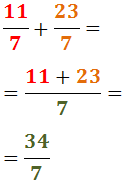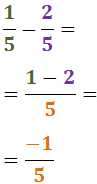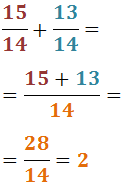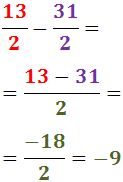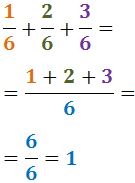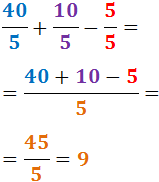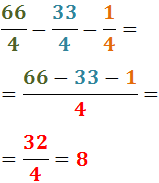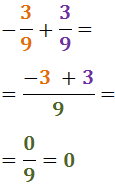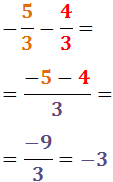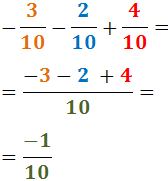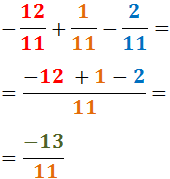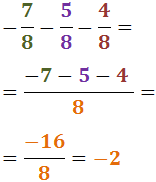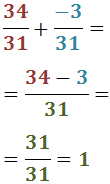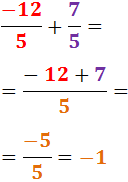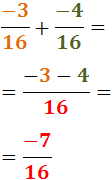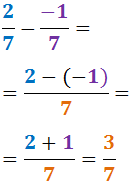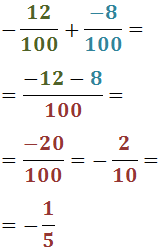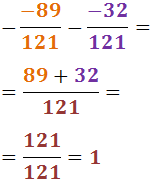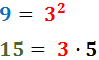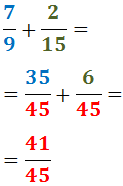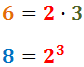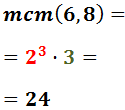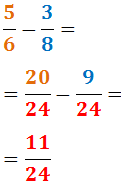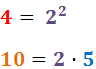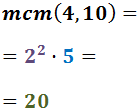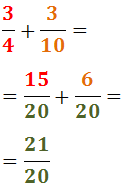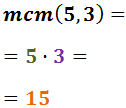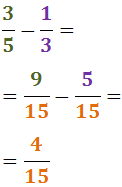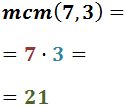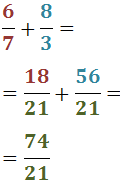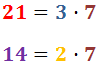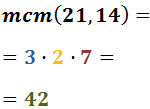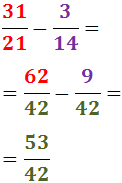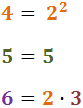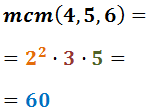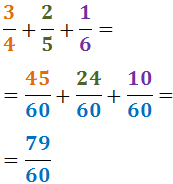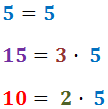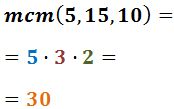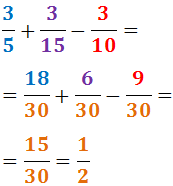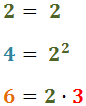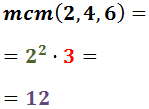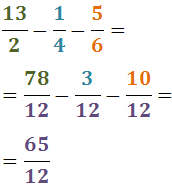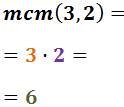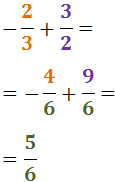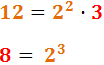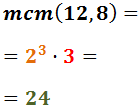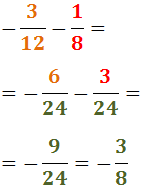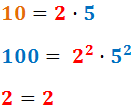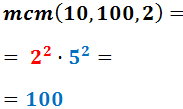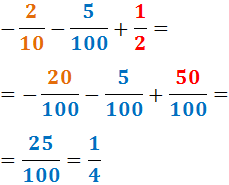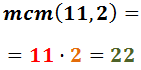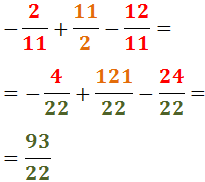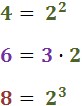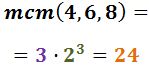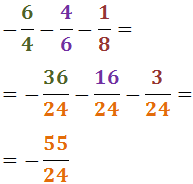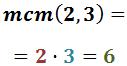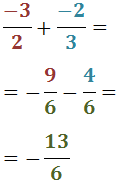Sumar i Restar Fraccions: Exercicis Resolts
|
Contingut d'aquesta pàgina:
-
Breu Introducció
-
Operacions entre Fraccions amb el mateix denominador i amb denominador distint
-
Suma de Fraccions Negatives i Fraccions amb diversos signes Negatius
-
Exercicis Resolts: Calcular sumes i restes de Fraccions
Novetat!
Intel·ligència artificial
Com els algorismes condicionen les nostres vides
Enric Senabre, Vicent Costa
Més informació: sembra llibres.
|
 |
Introducció
Com que les fraccions representen nombres (generalment, nombres decimals), té
sentit que puguem realitzar operacions entre fraccions: sumar,
restar, multiplicar,
dividir, etc.
En aquesta pàgina anem a veure com sumar i restar fraccions.
En les dues operacions distingirem dos casos:
En qualsevol cas, no oblidem que sempre hem de simplificar
el resultat.
Amb el Mateix Denominador
Com la suma
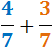
Veure Operacions
Suma
El denominador es manté. Només hem de sumar els numeradors.
Exemple:
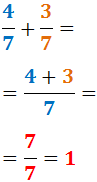
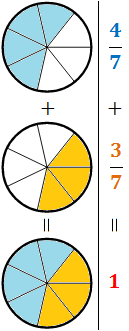
Representació gràfica:
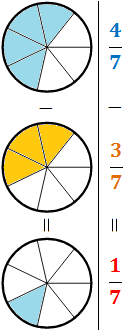
Resta
Només hem de restar els numeradors.
Exemple:
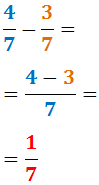
Representació gràfica:
Amb Distint Denominador
Com la suma
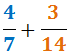
Veure Operacions
Tant per a sumar com per a restar, si els denominadors de les
fraccions no són el mateix, aleshores hem d'aconseguir que ho siguin.
El que farem en aquests casos és escriure una fracció equivalent a cadascun dels sumands. Vegem com:
Suma
Calculem el mínim comú múltiple dels denominadors
(factors comuns i no comuns al major exponent)
Exemple:
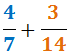
La descomposició de 14 en nombres primers és:
$$ 14 = 7 \cdot 2 $$
El nombre 7 no es pot descompondre en primers ja que ell mateix és un nombre
primer.
Els factors que apareixen en les descomposicions són 2 i 7, tots dos
amb exponent 1.
El mínim comú múltiple és el producte de tots els
factors al major exponent. Per tant, el mínim comú múltiple de 7 i 14 és
En el denominador de cada fracció
escrivim el mínim comú múltiple obtingut:
Exemple (continuació):
-
En el numerador de cada fracció escrivim el
resultat de dividir el mínim comú múltiple (el nou denominador)
entre el denominador inicial i multiplicar-lo pel numerador inicial:
Exemple (continuació):
El denominador inicial de la primera fracció era 7
i el numerador inicial era 4:
El denominador inicial de la segona fracció era 14 i el numerador inicial era 3:
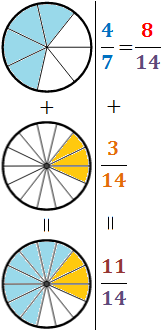
Per tant,
Com que els denominadors són iguals, sumem els numeradors:
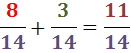
Representació gràfica:
Resta
De la mateixa manera que en la suma, fem que els denominadors siguin el mateix:
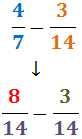
Com que els denominadors són iguals, restem els numeradors:
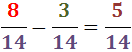
Representació gràfica:

Mètode alternatiu (distints denominadors)
Veure Mètode
Un mètode alternatiu per aconseguir el mateix
denominador és multiplicar en el numerador i el denominador
de cada fracció pel denominador de l'altra fracció.
Exemple:
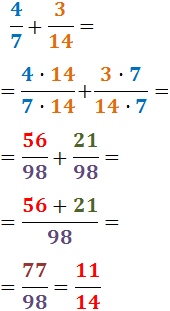
Recomanem el mètode anterior (el del mínim comú múltiple) ja que en el que acabem de veure
No obstant això, podem triar el mètode que preferim ja que els dos són correctes.
Suma de Fraccions Negatives
Veure Text
Quan les dues fraccions a sumar són negatives
es procedeix de la mateixa manera que en els casos
anteriors però, en el numerador tindrem la suma de dos nombres
negatius.
Hem de realitzar les operacions que realitzem quan es tracta de nombres enters.
Exemple (mateix denominador):
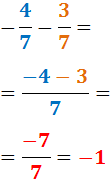
Exemple (distint denominador):
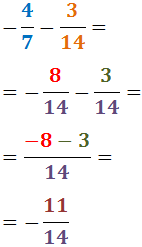
Operacions entre Fraccions amb signes Negatius
Com
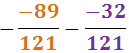
Veure Text
Una fracció pot tenir un signe negatiu en el numerador
i/o en el denominador i/o davant de la fracció:
-
Si només té un signe negatiu, la fracció és negativa:
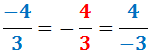
-
Si té dos signes negatius, la fracció és positiva:
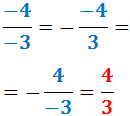
-
Si els signes són positius, la fracció és positiva (normalment, no trobarem
fraccions escrites d'aquesta manera ja que el signe positiu es sol reservar per
indicar una suma):
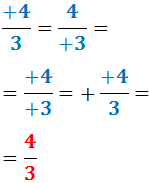
Els casos anteriors són el resultat d'aplicar la regla
dels signes (del producte).
Exercicis Resolts
Exercici A
Calcular les següents sumes i restes de fraccions amb denominador comú i
simplificar, si és possible, el resultat.
Exercici 1
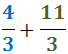
Veure solució
Exercici 2
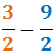
Veure solució
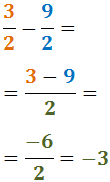
Notem que el signe negatiu es manté.
Exercici 3
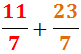
Veure solució
Exercici 4
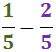
Veure solució
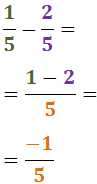
Notem que l'operació es redueix a una operació entre enters: com que tenen els signes
distints, mantenim el signe del major.
Exercici 5
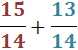
Veure solució
Exercici 6
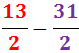
Veure solució
Exercici 7
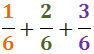
Veure solució
Exercici 8
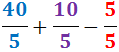
Veure solució
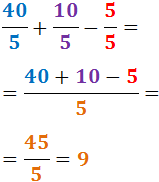
Notem que les tres fraccions es poden simplificar abans de sumar i restar:
$$ \frac{40}{5} = 8 $$
$$ \frac{10}{5} = 2$$
$$ \frac{5}{5} = 1$$
Per tant
$$ \frac{40}{5} + \frac{10}{5} + \frac{5}{5} = $$
$$ = 8 + 2 -1 = 9 $$
Exercici 9
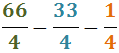
Veure solució
Exercici 10
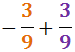
Veure solució
Exercici 11
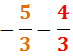
Veure solució
Com que les dues fraccions són negatives, haurem de sumar els numeradors i deixar
el signe negatiu:
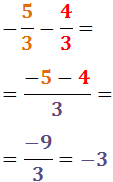
Exercici 12
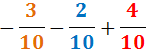
Veure solució
Exercici 13
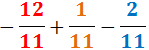
Veure solució
Exercici 14
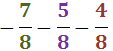
Veure solució
Exercici 15
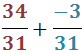
Veure solució
Exercici 16
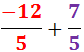
Veure solució
Exercici 17
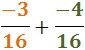
Veure solució
Exercici 18
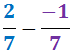
Veure solució
Notem que tenim un signe negatiu davant de la fracció i altre en el numerador: com que tenim
dos signes negatius, la fracció és positiva (és a dir,
podem treure els dos signes negatius i
escriure'n un positiu).
Nosaltres tractarem els signes com en una operació entre enters:
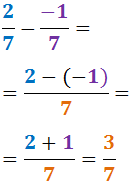
Exercici 19
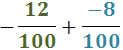
Veure solució
Notem que les dues fraccions són negatives: una té el signe negatiu davant
i l'altra el té al numerador.
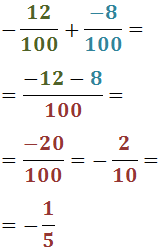
L'última fracció és el resultat de dividir primer entre 10 i després entre 2 (numerador i denominador) per
simplificar la fracció.
Exercici 20
Veure solució
En quest exercici les dues fraccions són positives perquè les dos tenen dos signes negatius.
Hem de tenir en compte que al treure els dos signes negatius haurem d'afegir-ne un positiu
entre les dues fraccions per indicar que s'han de sumar:
Exercici B
Calcular les següents sumes i restes de fraccions amb distint denominador i
simplificar, si és possible, el resultat.
Exercici 1
Veure solució
Descomponem els denominadors:
Per tant, el mínim comú múltiple és:

Reescrivim les fraccions i calculem l'operació:
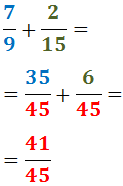
Exercici 2
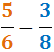
Veure solució
Descomponem els denominadors:
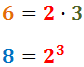
Per tant, el mínim comú múltiple és:
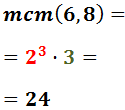
Reescrivim les fraccions i calculem l'operació:
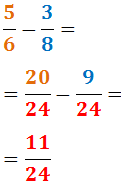
Exercici 3
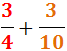
Veure solució
Descomponem els denominadors:
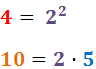
Per tant, el mínim comú múltiple és:
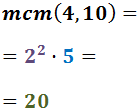
Reescrivim les fraccions i calculem l'operació:
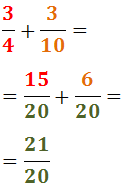
Exercici 4
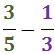
Veure solució
No descomponem els denominadors perquè 5 i 3 són nombres primers.
Per tant, el mínim comú múltiple és:
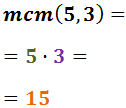
Reescrivim les fraccions i calculem l'operació:
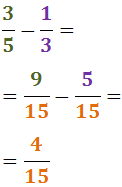
Exercici 5
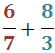
Veure solució
No descomponem els denominadors perquè 7 i 3 són nombres primers.
Per tant, el mínim comú múltiple és:
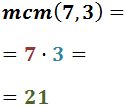
Reescrivim les fraccions i calculem l'operació:
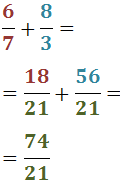
Exercici 6
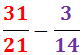
Veure solució
Descomponem els denominadors:
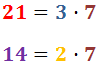
Per tant, el mínim comú múltiple és:
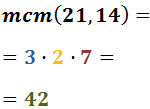
Reescrivim les fraccions i calculem l'operació:
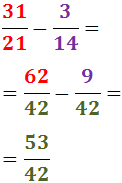
Exercici 7
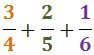
Veure solució
Descomponem els denominadors:
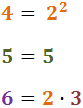
Per tant, el mínim comú múltiple és:
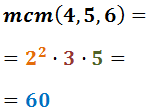
Reescrivim les fraccions i calculem l'operació:
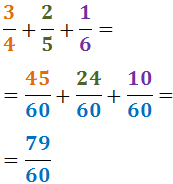
Exercici 8
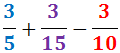
Veure solució
Descomponem els denominadors:
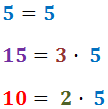
Per tant, el mínim comú múltiple és:
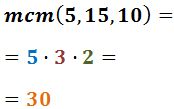
Reescrivim les fraccions i calculem l'operació:
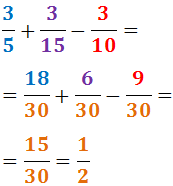
L'última fracció és el resultat de dividir entre 15 (numerador i denominador) per
simplificar la fracció.
Exercici 9
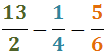
Veure solució
Descomponem els denominadors:
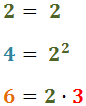
Per tant, el mínim comú múltiple és:
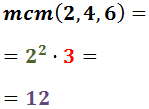
Reescrivim les fraccions i calculem l'operació:
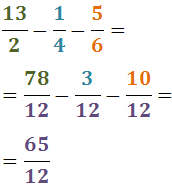
Exercici 10
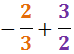
Veure solució
No descomponem els denominadors perquè 3 i 2 són nombres primers.
Per tant, el mínim comú múltiple és:
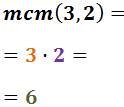
Reescrivim les fraccions i calculem l'operació:
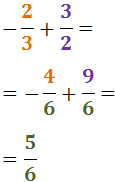
Exercici 11
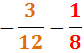
Veure solució
Descomponem els denominadors:
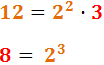
Per tant, el mínim comú múltiple és:
Reescrivim les fraccions i calculem l'operació:
L'última fracció és el resultat de dividir entre 3 (numerador i denominador) per
simplificar la fracció.
Exercici 12
Veure solució
Descomponem els denominadors:
Per tant, el mínim comú múltiple és:
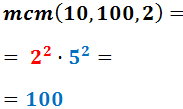
Reescrivim les fraccions i calculem l'operació:
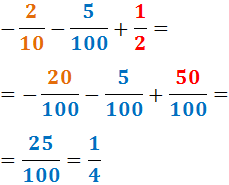
L'última fracció és el resultat de dividir entre 25 (numerador i denominador) per simplificar la fracció.
Exercici 13
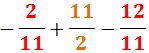
Veure solució
No descomponem els denominadors perquè 11 i 2 són nombres primers.
Per tant, el mínim comú múltiple és:
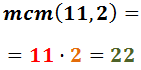
Reescrivim les fraccions i calculem l'operació:
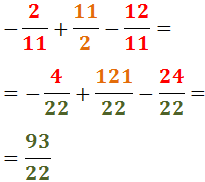
Exercici 14
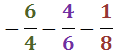
Veure solució
Descomponem els denominadors:
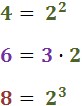
Per tant, el mínim comú múltiple és:
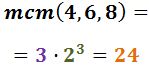
Reescrivim les fraccions i calculem l'operació:
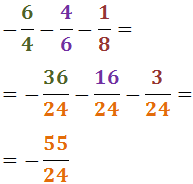
Exercici 15
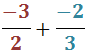
Veure solució
No descomponem els denominadors 2 i 3 perquè són nombres primers.
Per tant, el mínim comú múltiple és:
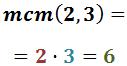
Reescrivim les fraccions i calculem l'operació:
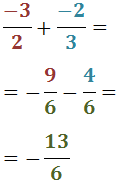

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.