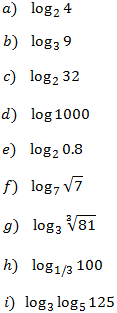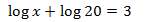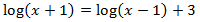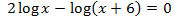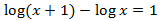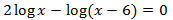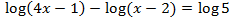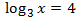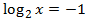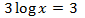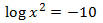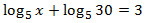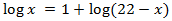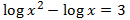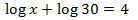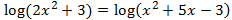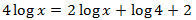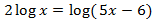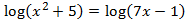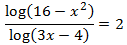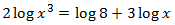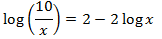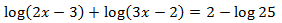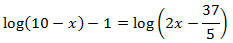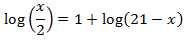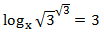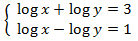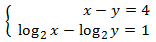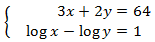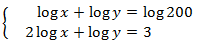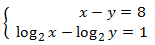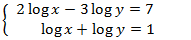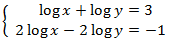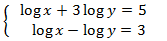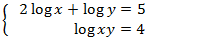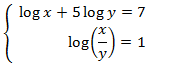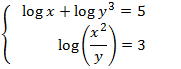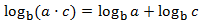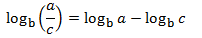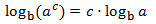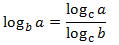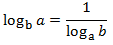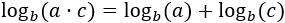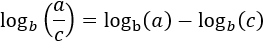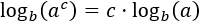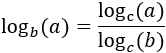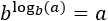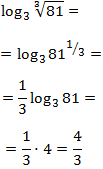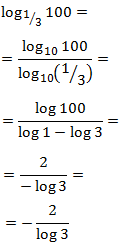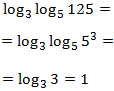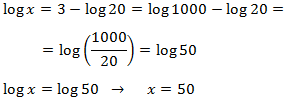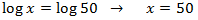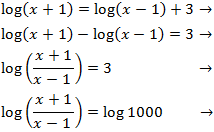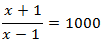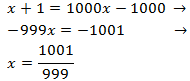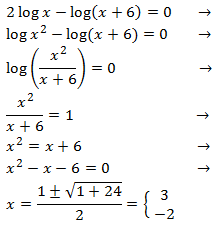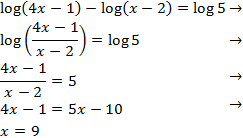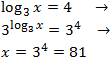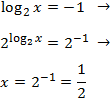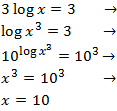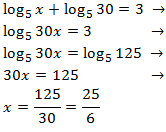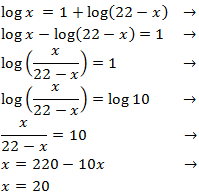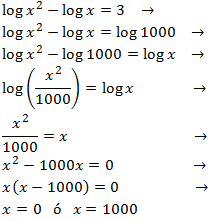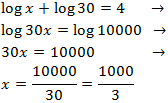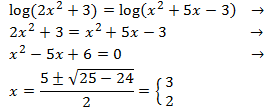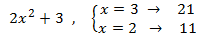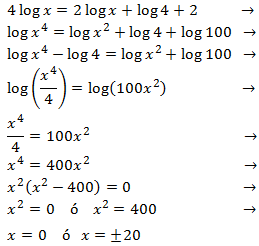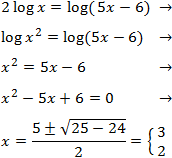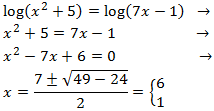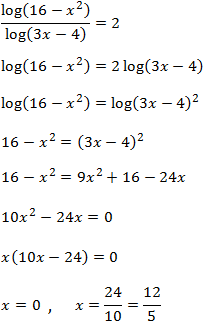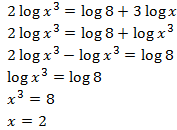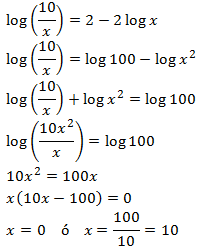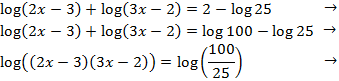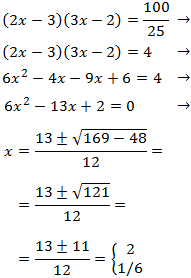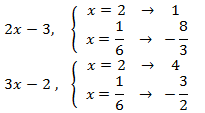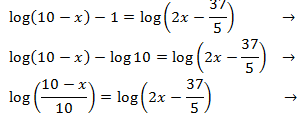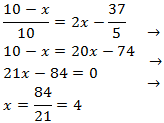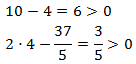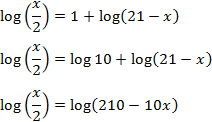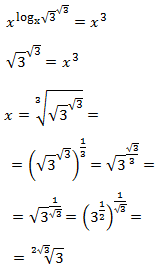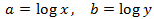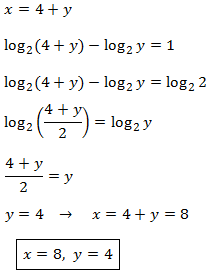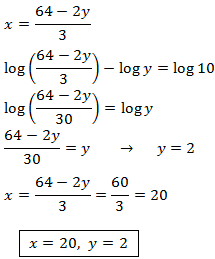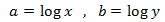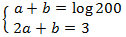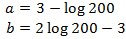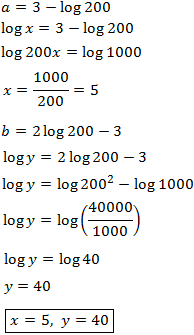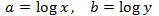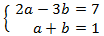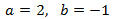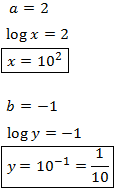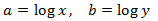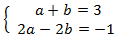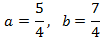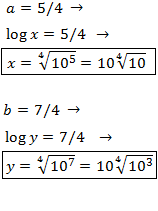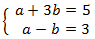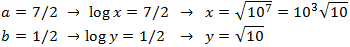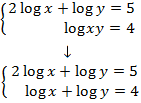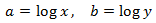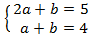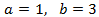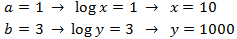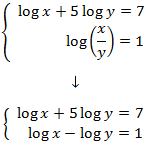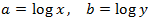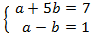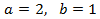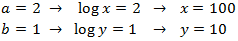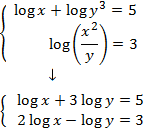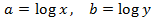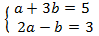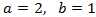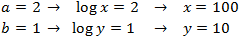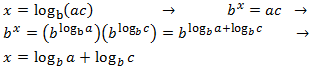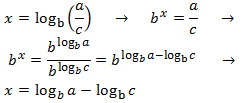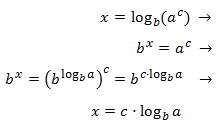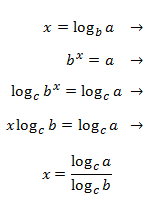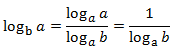Logaritmes:
Equacions, sistemes i demostracions
Contingut d'aquesta pàgina:
Breu introducció
Propietats dels logaritmes
-
25 Equacions logarítmiques resoltes
-
11 Sistemes resolts (d'equacions logarítmiques)
Demostració de les propietats dels logaritmes
Novetat!
Intel·ligència artificial
Com els algorismes condicionen les nostres vides
Enric Senabre, Vicent Costa
Més informació: sembra llibres.
|
 |
Introducció
En les equacions logarítmiques, la incògnita es troba
en l'argument de logaritmes. La seva resolució
es redueix, en realitat, a la resolució
d'equacions del mateix tipus que les
expressions dels arguments (equacions
de segon grau, tercer grau, irracionals...)
Aquesta secció és una col·lecció d'exercicis
resolts d'equacions i sistemes d'equacions
logarítmiques. En
la majoria dels logaritmes no s'especifica
la base perquè pressuposem que és 10.
Encara que cal dir que normalment en
els textos científics es considera, si
no s'indica el contrari, que la base és e
(és a dir, són logaritmes neperians).
A més, al final de la pàgina demostrarem
les propietats dels logaritmes: logaritme del producte, del
quocient, de la potència i el canvi
de base.
Pel que fa a les aplicacions dels logaritmes,
podem comentar que s'empren amb freqüència en
la física. Apareixen, per exemple, al calcular
la magnitud
aparent d'un cos celest (mesura de la quantitat de llum que percebem);
la magnitud d'un
terratrèmol en l'escala de Richter;
l'edat (el temps
transcorregut) en la datació
radiomètrica (com la prova del carboni 14); el pH.
Abans de començar amb els exercicis, recordem la definició del logaritme:
$$ log_b (a) = c \Leftrightarrow b^c = a $$
I les seves propietats:
logaritme del producte:
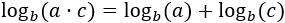
|
logaritme del quocient:
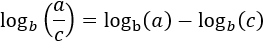
|
logaritme de la potència:
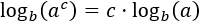
|
canvi de base:
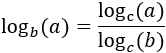
|
Propietat útil en la pràctica (definició de logaritme):
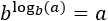
|
25 Equacions logarítmiques resoltes
Exercici previ
Calcular els següents logaritmes:
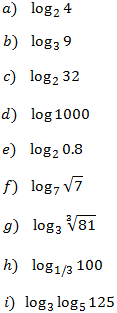
Mostrar solució
-
$$ log_2(4) = $$
$$ =log_2(2^2) = 2 $$
-
$$ log_3(9) = $$
$$ = log_3 (3^2) = 2$$
-
$$ log_2 (32) = $$
$$ = log_2(2^5) = 5 $$
-
$$ log(1000) =$$
$$ = log_{10} (1000)= $$
$$ =log_{10}(10^3) =3 $$
-
$$ log_2(0.8) = $$
$$ =log_2 \left( \frac{8}{10} \right) =$$
$$ = log_2 (8) - log_2(10) = $$
$$ = log_2 (2^3) - log_2(2·5) = $$
$$ = 3 -( log_2 (2·5) ) = $$
$$ = 3 - (log_2(2) + log_2(5))= $$
$$ = 3 - (1+log_2(5)) = $$
$$ = 2 -log_2(5) $$
-
$$ log_7(\sqrt{7}) = log_7(7^{\frac{1}{2}}) = $$
$$ \frac{1}{2} \cdot log_7(7) = $$
$$= \frac{1}{2}\cdot 1 $$
-
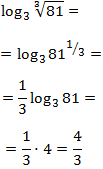
-
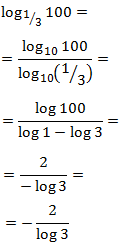
-
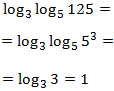
Equació 1
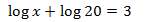
Mostrar solució
Emprarem les propietats dels logaritmes i que
$$log (1000) = log (10^3) = 3$$
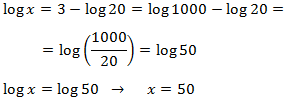
Tenim una igualtat entre logaritmes, aleshores els arguments (el de dins) han de
ser els mateixos
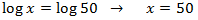
La solució és x = 50.
Equació 2
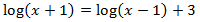
Mostrar solució
Emprarem la propietat del logaritme del quocient i escrivim 3 com
$$3=log(10^3)=log(1000)$$
per aconseguir una igualtat de logaritmes
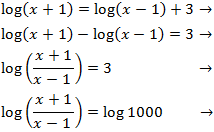
Els logaritmes són iguals quan els seus arguments (el de dins) són els iguals. és a dir,
volem
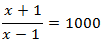
Resolem l'equació
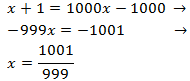
Ara tenim que comprovar que per a la solució obtinguda els arguments són
positius (perquè existeixin els logaritmes).
$$x+1 = \frac{1001}{99} > 0 $$
$$x-1 = \frac{1001}{99}-1 \simeq 0.002 >0 $$
per tant, és la solució.
Equació 3
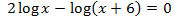
Mostrar solució
En aquesta equació, al aplicar les propietats per obtenir una igualtat de logaritmes
tindrem que resoldre una equació de segon grau:
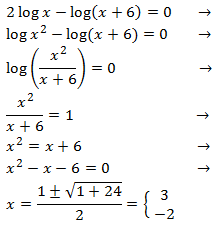
Notem que l'única solució possible és x = 3 ja que els arguments han de ser positius.
Equació 4
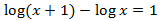
Mostrar solució
Fem servir les propietats dels logaritmes i que log(10) = 1:
$$ log(x+1)-log(x)=1 \rightarrow $$
$$ log\left( \frac{x+1}{x} \right) = log(10) \rightarrow $$
$$ \frac{x+1}{x} =10 \rightarrow $$
$$ x+1= 10x \rightarrow $$
$$ 9x = 1 \rightarrow $$
$$ x=\frac{1}{9} $$
Equació 5
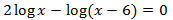
Mostrar solució
$$ 2log(x)-log(x-6)=0 $$
$$ log(x^2) = log(x-6) $$
Perquè els logaritmes siguin iguals es necessita que
$$ x^2 = x-6 $$
Resolem l'equació de segon grau:
$$ x^2 -x +6 = 0 $$
$$ x=\frac{1\pm \sqrt{1-24}}{2} $$
Com que el discriminant és negatiu (-23), no hi ha solucions (reals).
Per tant, no existeix solució.
Equació 6
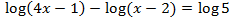
Mostrar solució
Equació 7
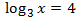
Mostrar solució
Com que tenim que dos termes són iguals, 3 elevat a aquests termes
serà el mateix nombre:
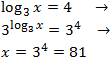
Elevem 3 ja que 3 és la base del logaritme.
Equació 8
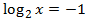
Mostrar solució
Equació 9
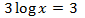
Mostrar solució
Equació 10
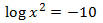
Mostrar solució
Com que el dos nombres son iguals (el logaritme i el nombre -10), aleshores, si elevem la base (10) a aquests
termes, també seran iguals:
$$ 10^{log(x^2)} = 10^{-10} $$
$$ x^2 = 10^{-10} = \frac{1}{10^{10}} $$
Per tant, fent l'arrel quadrada:
$$ x = \pm \sqrt{\frac{1}{10^{10}}} = $$
$$ = \pm \frac{1}{10^5} $$
Com que l'argument del logaritme és x al quadrat, ambdós valors són
solució de l'equació ja que al elevar al quadrat són nombres positius.
Equació 11
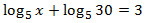
Mostrar solució
Emprarem el fet que
$$ 3 = log_5(125) $$
Per tant,
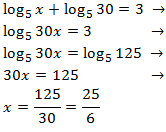
Equació 12
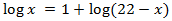
Mostrar solució
Sabem que
$$ log(10) = 1$$
Per tant
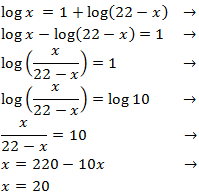
Equació 13
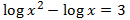
Mostrar solució
Utilitzarem el fet que
$$ log(1000) = 3 $$
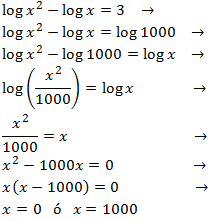
L'única solució és x = 1000 ja que l'argument d'un logaritme no mai
pot ser zero.
Equació 14
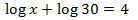
Mostrar solució
Escrivim 4 com un logaritme
$$ log(10000) = log(10^4) = 4 $$
Aleshores
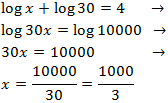
Equació 15
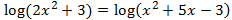
Mostrar solució
Igualem els arguments (el de dins del logaritme) i resolem l'equació de segon grau:
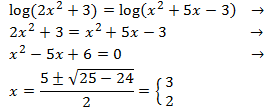
Les solucions d'aquesta equació, x = 3 i x = 2, són els valors
de x que fan que els arguments dels logaritmes siguen el mateix i, per tant,
la igualtat entre els logaritmes sigui vertadera. Però, hem de comprovar que els arguments siguin positius:
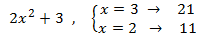
En efecte, ho són. Llavors són les solucions de l'equació logarítmica.
Equació 16
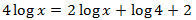
Mostrar solució
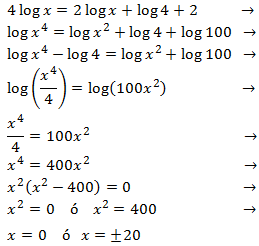
L'única solució possible és x = 20 ja que l'argument d'un logaritme
ha de ser necessàriament positiu.
Equació 17
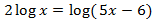
Mostrar solució
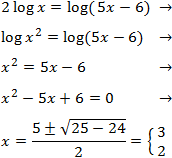
Les dues arrels de l'equació són solucions de l'equació logarítmica
ja que els arguments són positius.
Equació 18
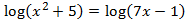
Mostrar solució
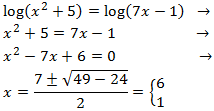
Tenim dues solucions ja que els arguments són positius.
Equació 19
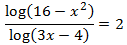
Mostrar solució
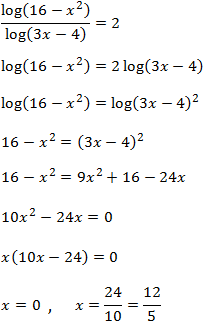
L'única solució és
$$ x = \frac{12}{5} $$
perquè si x = 0, l'argument del logaritme del denominador és negatiu.
Equació 20
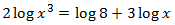
Mostrar solució
Equació 21
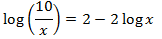
Mostrar solució
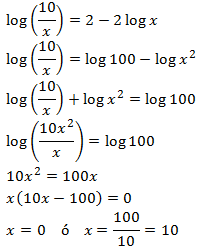
L'única solució és x = 10.
Equació 22
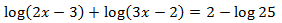
Mostrar solució
Emprarem les propietats dels logaritmes i que
$$2 = log (10^2)= log(100)$$
per obtenir una igualtat de logaritmes:
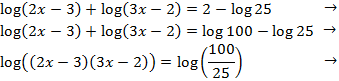
com que ja tenim la igualtat de logaritmes, valdran el mateix quan tinguin
el mateix argument, per tant, obtenim la equació de segon grau:
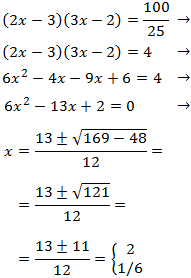
Ara comprovem si per a aquestes dues (possibles) solucions els arguments són positius:
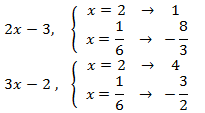
per tant, l'única solució és x = 2.
Equació 23
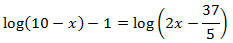
Mostrar solució
Escrivim 1 com
$$1 = log(10)$$
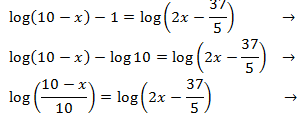
com que tenim una igualtat de logaritmes (amb la mateixa base), igualem els seus arguments i
resolem l'equació
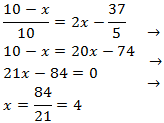
Ara comprovem que els arguments són positius:
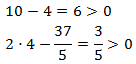
Equació 24
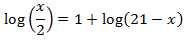
Mostrar solució
Equació 25
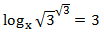
Mostrar solució
En aquesta equació tenim la incògnita en la base del logaritme. El que farem és utilitzar la definició
del logaritme per calcular-la. és a dir, emprarem la següent propietat:
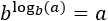
aleshores,
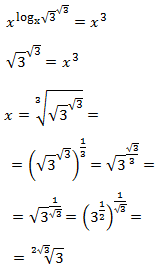
11 Sistemes Resolts
Sistema 1
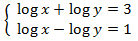
Mostrar solució
Apliquem el següent canvi de variable:
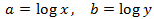
Obtenim el sistema d'equacions lineals
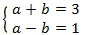
El resolem i desfem el canvi de variable
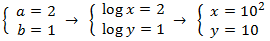
Sistema 2
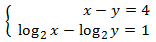
Mostrar solució
Notem que la primera equació del sistema no és logarítmica.
Aïllem x en la primera equació i la substituïm en la segona:
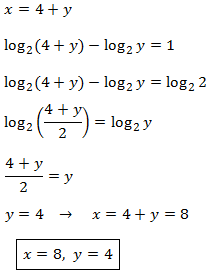
Sistema 3
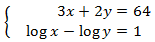
Mostrar solució
Aquest sistema és semblant al de l'exercici anterior:
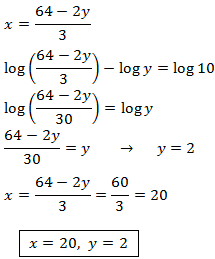
Sistema 4
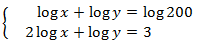
Mostrar solució
Apliquem el següent canvi de variable:
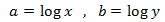
El sistema resultant és
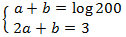
Les solucions d'aquest sistema són:
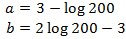
Ara desfem el canvi de variable i obtenim la solució del
sistema original:
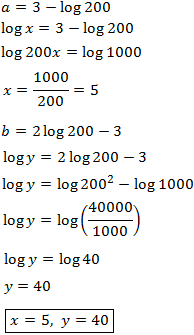
Sistema 5
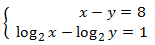
Mostrar solució
Sistema 6
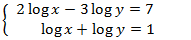
Mostrar solució
Apliquem el següent canvi de variable:
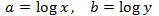
El sistema resultant és
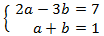
Les solucions d'aquest sistema són:
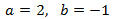
Ara desfem el canvi de variable i obtenim la solució del
sistema original:
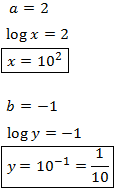
Sistema 7
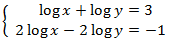
Mostrar solució
Apliquem el següent canvi de variable:
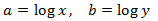
El sistema resultant és
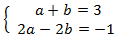
Les solucions d'aquest sistema són:
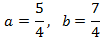
Desfem el canvi de variable i obtenim la solució del
sistema original:
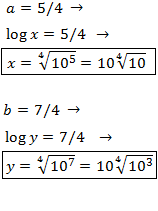
Sistema 8
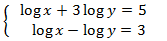
Mostrar solució
Apliquem el canvi de variable:

obtenint el següent sistema d'equacions lineals
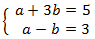
la solució del qual és

Finalment, desfem el canvi de variable:
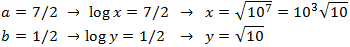
No és necessari comprovar les solucions ja que són positives.
Sistema 9
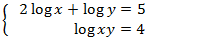
Mostrar solució
Emprem la propietat del logaritme del producte
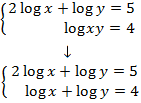
Ara apliquem el canvi de variable
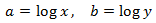
Obtenim així el sistema d'equacions
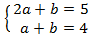
amb solució
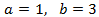
Només cal desfer el canvi de variable:
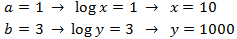
No és necessari comprovar les solucions ja que són positives.
Sistema 10
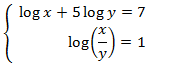
Mostrar solució
Primer apliquem la propietat del quocient del logaritme
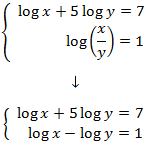
Apliquem el canvi de variable habitual:
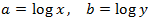
obtenint el següent sistema d'equacions lineals
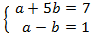
que té per solució
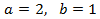
Per acabar, desfem el canvi de variable
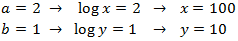
No cal comprovar les solucions.
Sistema 11
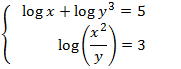
Mostrar solució
Emprem la propietat del logaritme del quocient i de la potència
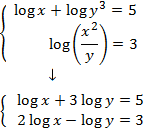
Ara apliquem el canvi de variable com de costum
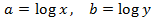
Obtenint el sistema d'equacions
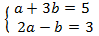
que té per solució
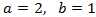
Desfem el canvi de variable:
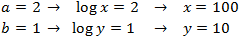
Demostració de les propietats dels logaritmes
Propietat 1: logaritme del producte
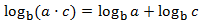
Mostrar demostració
Propietat 2: logaritme del quocient
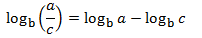
Mostrar demostració
Propietat 3: logaritme de la potència
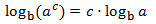
Mostrar demostració
Propietat 4: canvi de base
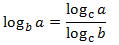
Mostrar demostració
Propietat 5: invers del logaritme
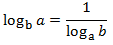
Mostrar demostració

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.