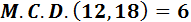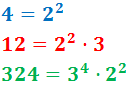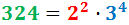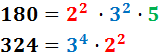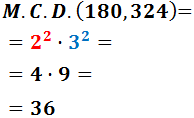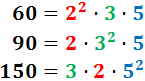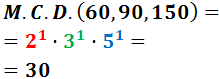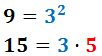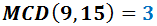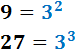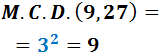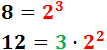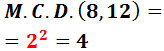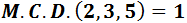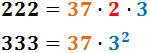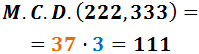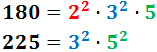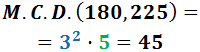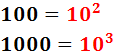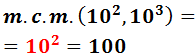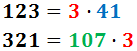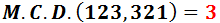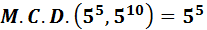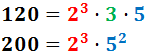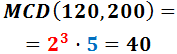Màxim Comú Divisor |
Contingut d'aquesta pàgina:
-
Concepte de Màxim Comú Divisor (MCD)
-
Descomposició en nombres primers (recordatori)
-
Mètode per l'obtenció del MCD a partir de la descomposició
-
Test i Exercicis resolts: calcular el MCD de dos o tres nombres, preguntes teòriques i problemes d'aplicació
Novetat!Intel·ligència artificialCom els algorismes condicionen les nostres videsEnric Senabre, Vicent Costa Més informació: sembra llibres. |
 |
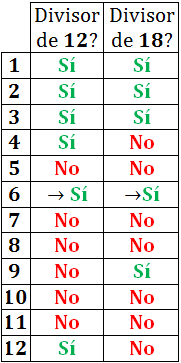
1. Definició i Exemple
2. Descomposició en Nombres Primers
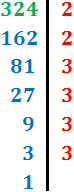
Anem a recordar com descompondre nombres per escriure'ls com un producte de nombres primers, la qual cosa facilitarà el càlcul del màxim comú divisor:
3. Obtenció del MCD a partir de les descomposicions
Regla per al MCD:
«comuns al menor exponent»
4. El MCD de més de dos nombres
Exercicis Resolts de Màxim Comú Divisor: Test i Problemes
Exercici 1
El màxim comú divisor de 9 i 15 és...
Triar l'opció correcta:
|
9, perquè el MCD no pot ser major que els nombres
|
|
|
1, perquè divideix als dos nombres
|
|
|
3, perquè és el major divisor dels nombres
|
Raonament:
Exercici 2
El màxim comú divisor de 9 i 27 és...
|
3, perquè 9 i 27 són potències de 3
|
|
|
9, perquè divideix a 9 i a 27 i el seu MCD ha de ser menor o igual que 9 i que 27
|
|
|
27, perquè és el MCD ha de ser màxim
|
Raonament:
Exercici 3
El màxim comú divisor de 2, 3 i 4 és...
|
1, perquè es no hi ha altre divisor comú de 2 i de 3
|
|
|
12, perquè és múltiple dels tres nombres
|
|
|
2, perquè és el MCD ha de ser menor o igual que 2, 3 i 4
|
Raonament:
Exercici 4
El màxim comú divisor de 8 i 12 és...
|
1
|
|
|
4
|
|
|
8
|
Raonament:
Exercici 5
El màxim comú divisor de 2, 3 i 5 és...
|
0
|
|
|
1
|
|
|
6
|
Raonament:
Exercici 6
El màxim comú divisor de 222 i 333 és...
|
111
|
|
|
222
|
|
|
333
|
Raonament:
Exercici 7
El màxim comú divisor de 180 i 225 és...
|
12
|
|
|
45
|
|
|
85
|
Raonament:
Exercici 8
El màxim comú divisor de 100 i 1000 és...
|
10
|
|
|
100
|
|
|
1000
|
Raonament:
Exercici 9
El màxim comú divisor de 123 i 321 és...
|
2
|
|
|
3
|
|
|
123
|
Raonament:
Exercici 10
El màxim comú divisor de 55 i 510 és...
|
55
|
|
|
510
|
|
|
515
|
Raonament:
Exercici 11
El màxim comú divisor de dos nombres primers és...
|
1
|
|
|
El nombre primer menor.
|
|
|
El producte dels nombres primers.
|
Raonament:
Exercici 12
El màxim comú divisor és 0 quan...
|
Un dels dos nombres és primer però l'altre no ho és.
|
|
|
Els dos nombres són una potència de la mateixa base.
|
|
|
No mai.
|
Raonament:
Exercici 13
El màxim comú divisor de dos nombres...
|
És múltiple dels dos nombres.
|
|
|
És sempre un nombre parell.
|
|
|
És menor o igual que els dos nombres.
|
Raonament:
Exercici 14
Si el màxim comú divisor de dos nombres és el 4...
|
Els dos nombres són una potència de 2.
|
|
|
Al menys un dels nombres és una potència de 2.
|
|
|
Els dos nombres són parells.
|
Raonament:
Exercici 15
Si el màxim comú divisor de dos nombres és senar, aleshores...
|
Els dos nombres són senars.
|
|
|
No podem deduir la paritat dels nombres,
és a dir, poden ser parells, senars o un parell i l'altre senar.
|
|
|
No poden ser parells els dos nombres, és a dir, o els dos són senars o un és parell i l'altre és senar.
|
Raonament:
Exercici 16
Tenim una corda de 120 metres i una altra de 200 metres. Volem tallar-les per obtenir altres cordes, totes de la mateixa longitud però, el més llargues possibles, de manera que no sobre cap tros.
Calcular la longitud de les cordes i el nombre total de cordes.
== Ajuda: ==
Exemple 1: podem tallar la de 200 m obtenint una de 120 m i una de 80 m. Però aquesta elecció no és correcta ja que no mesuren totes el mateix.
Exemple 2: si tallem en cordes d'1 m, totes mesuraran el mateix però seran massa curtes.
Exercici 17 (dificultat alta)
Considerem el MCD de dos nombres a i b.
Si els nombres a i b són divisibles pel nombre primer k (distint del MCD), aleshores...
|
k és divisible pel MCD.
|
|
|
el MCD és divisible per k.
|
|
|
No existeix relació de divisibilitat entre k i el MCD.
|
Raonament:
Exercici 18 (dificultat alta)
El MCD de dos nombres parells...
|
També és parell.
|
|
|
És senar.
|
|
|
No existeix cap relació.
|
Raonament:

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.