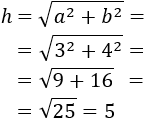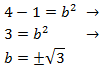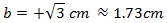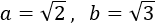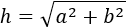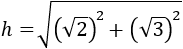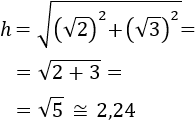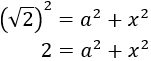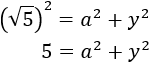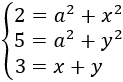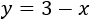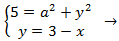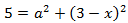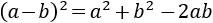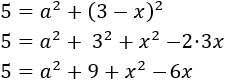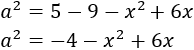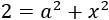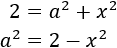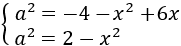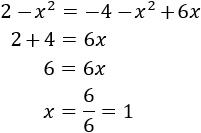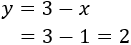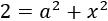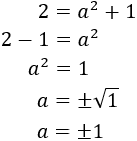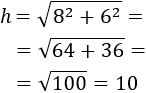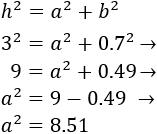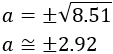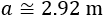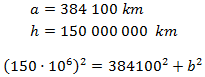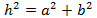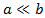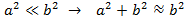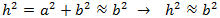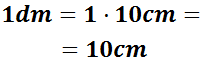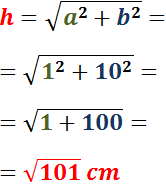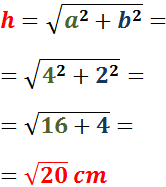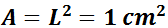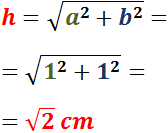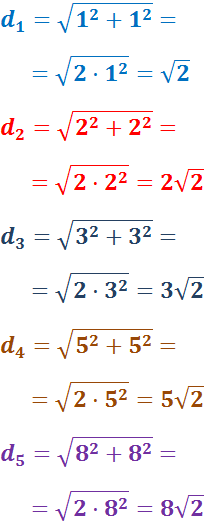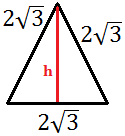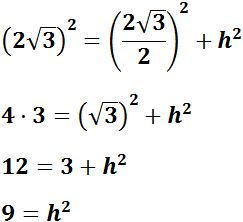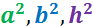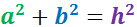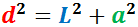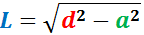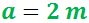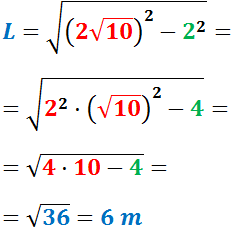Teorema de Pitàgores
Contingut d'aquesta pàgina:
-
Breu introducció
-
Problemes resolts d'aplicació del Teorema de Pitàgores
-
Test sobre el teorema de Pitàgores
Novetat!Intel·ligència artificialCom els algorismes condicionen les nostres videsEnric Senabre, Vicent Costa Més informació: sembra llibres. |
 |
Introducció
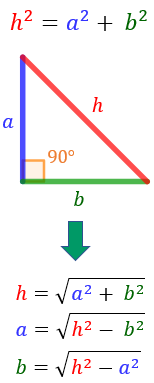
Teorema: donat un triangle rectangle amb catets a i b i hipotenusa h (el costat oposat a l'angle recte). Aleshores,
Recordem que:
-
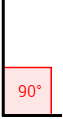
el triangle és rectangle perquè té un angle recte, és a dir, un angle de 90 graus ó π / 2 radiants.
-
la hipotenusa és el costat oposat a l'angle recte
Nota: h sempre és major que els dos catets, és a dir, h > a i h > b.
El teorema de Pitàgores és un dels resultats més coneguts de les matemàtiques i també un dels més antics amb cents de demostracions.
La piràmide de Kefrén (segle XXVI a. C.) fou construïda en base a l'anomenat triangle sagrat egipci, que és el triangle rectangle de costats 3, 4 i 5.
La comprensió del teorema de Pitàgores és senzilla i té moltes aplicacions en la vida quotidiana, com veurem als problemes d'aquesta secció. Però, també té les seves aplicacions en les matemàtiques avançades (com en l'anàlisi vectorial i l'anàlisi funcional).
Problemes Resolts
Problema 1
Calcular la hipotenusa del triangle rectangle de costats 3cm i 4cm.
Problema 2
Si la hipotenusa d'un triangle rectangle mesura 2cm i un dels seus costats mesura 1cm, quant mesura l'altre costat?
Problema 3
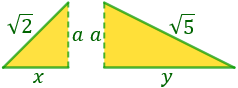
Calcular la hipotenusa del triangle rectangle amb costats de longitud 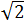 i
i 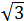 .
.
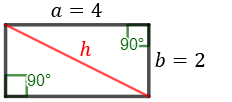
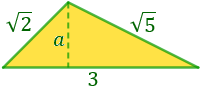
Problema 4 (dificultat alta)
Calcular l'altura del següent triangle sabent que els seus costats mesuren
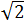 ,
,
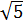 i la seva base 3.
i la seva base 3.
Problema 5
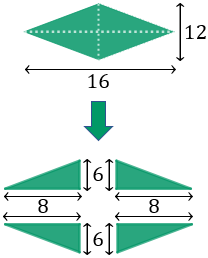
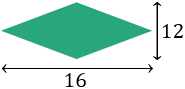
Calcular el perímetre del següent rombe si sabem que les seves diagonals (altura i amplària) mesuren 16 i 12.
Problema 6
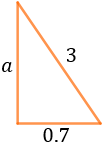
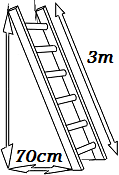
Calcular l'altura a la que podem arribar amb una escala de 3 metres d'altura recolzada sobre la paret si la part inferior la situem a 70 centímetres de la paret.
Problema 7 (dificultat alta)
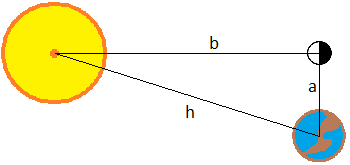
Distàncies Sol-Terra-Lluna.
Suposem que la Lluna està en la fase del seu primer quart, la qual cosa significa que des de la Terra la veiem de la següent manera

sent la meitat clara la que veiem, és a dir, la il·luminada pel Sol.
Sabem que la distància de la Terra a la Lluna és de 384100km i de la Terra al Sol és d'uns 150 milions de quilòmetres. Es vol calcular la distància de la Lluna al Sol en aquesta fase (considerar les distàncies des dels centres).
Plantejar el problema però no cal calcular el resultat.
Test
Tria l'opció correcta en totes les preguntes:
Pregunta 1
Un angle recte és...
|
Un angle de 45 graus.
|
|
|
Un angle de 90 graus.
|
|
|
Un angle de 180 graus.
|
Raonament:
Pregunta 2
Per poder aplicar el teorema de Pitàgores...
|
És necessari tenir un angle obtús.
|
|
|
És necessari tenir un angle recte.
|
|
|
És necessari tenir un triangle equilàter.
|
|
|
Totes les opcions anteriors són falses.
|
Raonament:
Pregunta 3
En un triangle rectangle de costats 1cm i 1dm, quant mesura la hipotenusa?
|
$$ \sqrt{101} \ cm $$ |
|
|
$$ \sqrt{202} \ cm $$
|
|
|
$$ \sqrt{101} \ dm $$
|
|
|
Totes les opcions anteriors són falses.
|
Raonament:
Pregunta 4
La diagonal d'un rectangle de costats 2cm i 4cm mesura...
|
(a) $$ \sqrt{20} \ cm $$
|
|
|
(b)$$ \sqrt{0,3} \ dm $$
|
|
|
Les opcions (a) i (b) són correctes.
|
|
|
Les opcions (a) i (b) són falses.
|
Raonament:
Pregunta 5
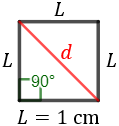
La diagonal d'un quadrat d'àrea 1cm2 mesura...
|
$$ 1\ cm $$
|
|
|
$$ 1\ dm $$
|
|
|
$$ \sqrt{2} \ cm $$
|
|
|
$$ \sqrt{3} \ dm $$
|
Raonament:
Pregunta 6
La següent figura està formada per dos rectangles (un és blau i l'altre és groc) i un triangle equilàter (tots els seus costats mesuren el mateix).
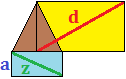
Sabem que un dels costats i la diagonal del rectangle blau mesuren:
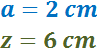
Es vol calcular quant mesura la diagonal de l'altre rectangle (d) aplicant el teorema de Pitàgores.
|
No és possible calcular la diagonal amb les dades que coneixem.
|
|
|
És possible calcular-la i mesura 7.5cm.
|
|
|
És possible calcular-la i mesura 11cm.
|
|
|
Ninguna de les opcions anteriors és certa.
|
Raonament:
Pregunta 7
La següent figura està formada per quadrats de distintes mides, sent el nombre que hi ha en cadascun dels quadrats la longitud dels seus costats (són els primers termes de la sèrie de Fibonacci).
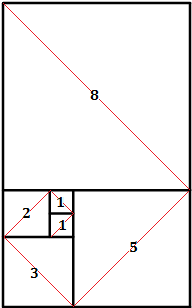
Es vol calcular la longitud de la corda de color vermell.
|
No es pot calcular la longitud amb les dades donades.
|
|
|
La longitud és $$20$$
|
|
|
La longitud és $$2\sqrt{20}$$
|
|
|
La longitud és $$20 \sqrt{2}$$
|
Raonament:
Pregunta 8
Volem calcular l'altura, h, d'un triangle equilàter de costat
$$ 2\sqrt{3} $$
La representació del triangle és
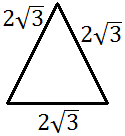
|
$$ h=1 $$
|
|
|
$$ h=2 $$
|
|
|
$$ h=3 $$
|
|
|
Totes les opcions anteriors són falses.
|
Raonament:
Pregunta 9
La següent figura
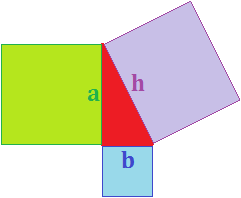
pot emprar-se per provar geomètricament el teorema de Pitàgores perquè...
|
L'àrea del quadrat morat és igual a l'àrea del triangle (color vermell).
|
|
|
La suma de les àrees dels quadrats morat i blau és igual a l'àrea del triangle (color vermell).
|
|
|
La suma de les àrees del triangle i del quadrat verd és igual a la suma de les àrees dels
quadrats blau i morat.
|
|
|
La suma de les àrees dels quadrats verd i blau és igual a l'àrea del quadrat morat.
|
Raonament:
Pregunta 10
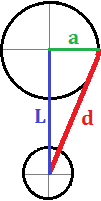
Els radis de les circumferències de la figura mesuren 1 i 2 metres
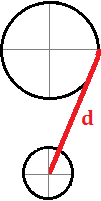
I el segment vermell que les uneix mesura
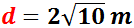
Es desitja calcular la distància, L, que hi ha entre els centres d'ambdues circumferències.
|
No podem calcular L, al menys aplicant Pitàgores, perquè les circumferències no tenen angles rectes.
|
|
|
La distància és L = 5 m.
|
|
|
La distància és L = 60 dm.
|
|
|
La distància és L = 0,5 cm.
|
Raonament:

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.