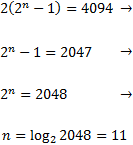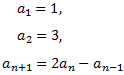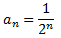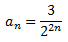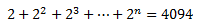Problema 1
En una seqüència aritmètica, sabem que el sext terme és 28 i que la diferència és 5. Calcular el terme general i els 5 primers termes.
Veure solució
Coneixem el terme 6-èsim i la diferència:
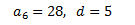
Volem calcular el terme general de la successió, \(a_n\), que sabem
que és de la forma
$$ a_n = a_1 + (n-1)\cdot d$$
Com que la diferència és \(d = 5\), tenim
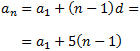
Necessitem calcular el primer terme de la successió, \(a_1\). Per a això, apliquem la fórmula per al cas \( n = 6\) ja que sabem que
\( a_6 = 28\). Substituïm en la fórmula:
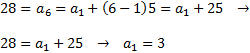
Per tant, el terme general de la successió aritmètica és
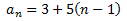
Els cinc primers termes són
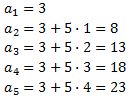
Nota: hem calculat els termes aplicant el terme general però, una
vegeda sabem que el primer terme és 3 i que la diferència és 5, també podem obtenir
els termes sumant 5:
\( a_ 1 = 3\)
\( a_ 2 = 3 + 5 = 8\)
\( a_ 3 = 8 + 5 = 13\)
\( a_ 4 = 13 + 5 = 18\)
\( a_ 5 = 18 + 5 = 23\)
Problema 2
En una seqüència geomètrica, sabem que el primer terme és 6 i el quart és 48. Calcular el terme general i la suma dels 5 primers termes.
Veure solució
Coneixem el primer i el quart terme:

Com que la seqüència és geomètrica, el seu terme general és de la forma
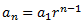
D'aquesta fórmula coneixem el terme \(a_1\) però, no coneixem la raó,
\(r\). Per calcular-la, apliquem la fórmula per al cas \(n=4\) perquè sabem
que \( a_4 = 48\):
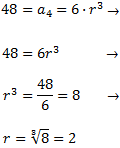
Per tant, la raó és \(r = 2\) i el terme general és
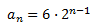
Per calcular la suma dels 5 primers termes, apliquem la fórmula. Necessitarem calcular el terme \(a_5\):
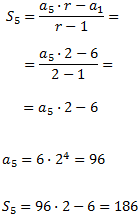
Problema 3
Trobar el terme general de la successió
20, 19.3, 18.6, 17.9, …
És aritmètica o geomètrica? Trobar els termes desè (10), vintè (20) i trentè (30).
Veure solució
Si la successió és aritmètica, aleshores la diferència entre dos
termes consecutius sempre és la mateixa.
Cerquem la diferència restant termes consecutius:
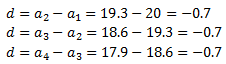
Es tracta d'una successió aritmètica amb diferència d = -0.7 (és una successió decreixent, d < 0). Per tant, el terme general és
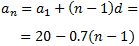
Aplicant la fórmula, podem calcular els terms desè, vintè i trentè:
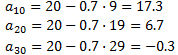
Problema 4
Trobar el terme general de la successió
0.5, 0.25, 0.125, 0.0625,...
És aritmètica o geomètrica? Calcular els termes n- èsims per als valors de n = 10, 100.
Es sap que la suma dels infinits termes d'aquesta successió és 1 (Problema 26). Raonar com és possible
que la suma d'infinits termes positius no sigui infinita.
Veure solució
Cerquem la diferència restant termes consecutius:
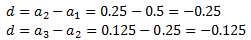
Com que les diferències no coincideixen, la successió no és aritmètica.
Cerquem la raó dividint termes consecutius:
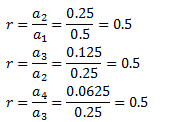
Es tracta d'una successió geomètrica amb raó r = 0.5 (decreixent ja que r < 1).
Com que coneixem el primer terme i la raó, podem obtenir el terme general:
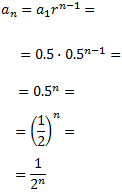
Llavors, podem calcular els termes 10-èsim i 100-èsim:
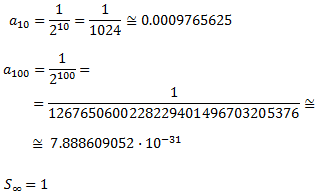
Observem que els termes de la successió són molt menuts: el desè té tres zeros
després de la coma i el centè en té trenta.
Encara que els termes de la successió siguin positius, són cada vegada més menuts i molt propers
a 0. Per això, al sumar-los, a penes augmenta el valor,
fins i tot, encara que en sumem infinits.
Problema 5
En una progressió aritmètica, sabem que el primer terme és 1 i la suma dels 10 primers termes és 63. Calcular el terme general.
Veure solució
Coneixem el primer terme i la suma dels deu primers termes:
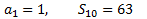
Utilitzarem les fórmules del terme general i de la suma (d'una seqüència aritmètica) per poder calcular la diferència, \(d\). Aquestes fórmules són:
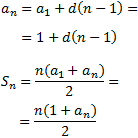
Hem escrit en les fórmules el primer terme \(a_1 = 1\).
Substituïm les dades conegudes:
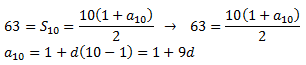
Podem substituir \( a_{10}\) en la primera fórmula:
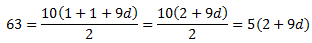
De l'equació resultant obtenim d:
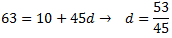
Llavors, la diferència és \(d = 53/45\) i el terme general és
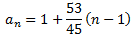
Problema 6
En una seqüència aritmètica finita, el
segon terme és -23 i l'últim és 32. Si
es sap que hi ha 12 termes, calcular el terme general.
Veure solució
Coneixem el segon terme i el 12-èsim:
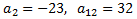
El fet que la successió sigui finita no canvia a l'hora de trobar el seu terme general.
Per ser aritmètica, sabem que el terme general de la seqüència és de la forma
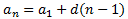
Amb les dades que tenim, podem construir un sistema d'equacions per calcular
el primer terme i la diferència:
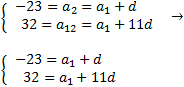
Resolem el sistema pel mètode d'igualació:
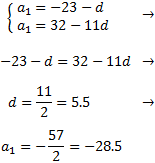
Per tant, el terme general és
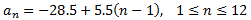
Nota: hem indicat els valors que pot ser n per fer notar que la successió és finita.
Problema 7
La suma de tres termes consecutius d'una successió aritmètica que té diferència 11 és 66. Trobar aquests termes.
Veure solució
Els nombres són
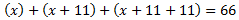
És a dir, tenim una equació de primer grau:

Llavors, els tres nombres són 11, 22 i 33.
L'equació la podem expressar en termes d'una seqüència com
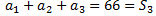
És a dir, com la suma dels tres primers termes d'una seqüència de terme general
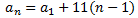
Problema 8
La suma de n nombres naturals
consecutius a partir de 55 (sense incloure'l) és 738. Trobar n.
Veure solució
El problema diu que
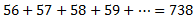
Hem de calcular \(n\), que és el nombre de sumands que hi ha a l'esquerra de la igualtat.
Podem expressar l'equació d'abans com
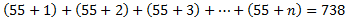
És a dir,
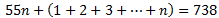
En realitat, l'interior del parèntesi és la
suma dels n primers termes d'una
seqüència aritmètica amb diferència 1 i amb
primer terme igual a 1, és a dir,
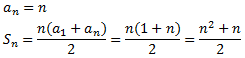
Per tant, podem reescriuire l'equació como
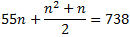
Tenim, aleshores, una equació de segon grau amb les solucions
n = -123 i n = 12. Com que n
representa la quantitat de sumands, ha de ser un
nombre natural (un enter positiu), de manera que ha de ser n = 12.
Problema 9
La suma de 6 nombres imparells i consecutius és 120. Trobar aquests nombres.
Veure solució
Un nombre imparell és de la forma
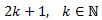
Per tant, cerquem el k que compleix
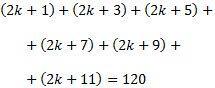
Simplificant,
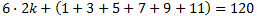
L'interior del parèntesi és la suma dels 6 primers termes d'una successió aritmètica de diferència 2 i que comença en 1, és a dir,
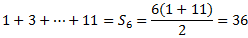
Per tant,
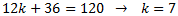
Els nombres són 15, 17, 19, 21, 23, 25.
Problema 10
Demostrar que en qualsevol successió geomètrica
positiva, cada terme és l'arrel quadrada del producte del seu
terme anterior pel seu terme següent. És a dir,
$$ a_n = \sqrt{a_{n-1}\cdot a_{n+1}}$$
Veure solució
El terme general d'una successió geomètrica és
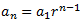
I volem demostrar que
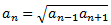
Per demostrar-ho, calculem \(a_{n-1}\) i \(a_{n+1}\) emprant el terme general:
$$a_{n-1} = a_1 r^{n-1-1} = a_1 r^{n-2} $$
$$a_{n+1} = a_1 r^{n+1-1} = a_1 r^{n} $$
Substituint en el radicant, estarà demostrat al obtenir que l'arrel és el terme \(a_n\):
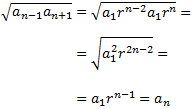
Observacions:
-
Hem aplicat les propietats de les potèncias per a simplificar.
-
L'exigència de que la successió sigui positiva és perquè, d'aquesta manera, l'arrel quadrada de \(a_1^2\) és \(a_1\) i no el seu valor absolut.
-
Com que la successió és positiva, la seua raó també ho és. Per això, tampoc
escrivim el valor absolut al simplificar l'arrel de \( r^{2(n-1)}\).
Problema 11
Una progressió geomètrica comença en 1 i té raó 2.
Trobar els tres termes consecutius (de la progressió) el producte dels quals és 512.
Veure solució
El terme general de la progressió és
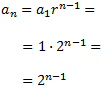
No sabem la posició que ocupen els tres termes però, sí que sabem
que són consecutius. Per tant, si el primer d'aquests és \(a_n\), els altres dos són \(a_{n+1}\) i \(a_{n+2}\).
Aleshores, emprant el terme general, el producte dels termes és
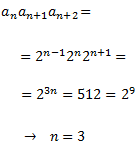
Llavors, els termes són el tercer, el quart i el cinquè: 4, 8, 16.
Problema 12
Trobar el terme general de la successió
1, 4, 9, 16, 25, 36, 49, ...
És aritmètica o geomètrica?
Veure solució
Comprovem si és aritmètica restant termes consecutius:
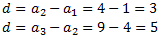
No ho és ja que les diferències no coincideixen.
Comprovem si és geomètrica dividint termes consecutius:
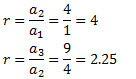
No ho és ja que la raó no és la mateixa.
Llavors, la seqüència no és ni aritmètica ni geomètrica. Hem de deduir pel nostre compte quin és el terme general.
El primer que fem és fixar-nos en la rel·lació que hi ha entre la posició de cada terme i seu valor:
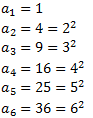
Per tant, deduïm que el terme general és
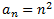
No és una seqüència aritmètica ni geomètrica.
En aquesta successió no podem utilitzar
la fórmula que coneixem per sumar \(n\) termes.
Problema 13
Trobar el terme general de la successió
1, 4, 27, 256, 3125, ...
És aritmètica o geomètrica?
Veure solució
Comprovem si és aritmètica:
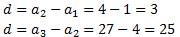
No ho és. Comprovem si és geomètrica:
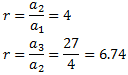
No ho és. Ens fixem en la rel·lació que hi ha entre la posició de cada terme i el seu valor:
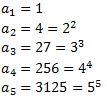
Per tant, deduïm que el terme general és
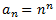
No és una seqüència aritmètica ni geomètrica.
Problema 14
Trobar el terme general de la successió
1, -2, 4, -8, 16,...
És aritmètica o geomètrica?
Veure solució
Comprovem si és aritmètica:
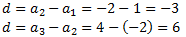
No ho és. Comprovem si és geomètrica:
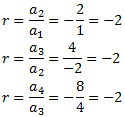
Per tant, és geomètrica amb raó r = -2 i, per tant, el seu terme general és
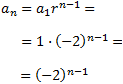
Com que la raó és negativa, la successió és alternada. Açò
implica que cada terme té un signe distint. En aquesta successió en particular, els termes de posició parella són negatius i els altres són positius.
Problema 15
Calcular la suma dels tres primers termes
d'una successió geomètrica de raó 0.5
sabent que el seu producte és 1000.
Veure solució
Com que la successió és geomètrica i coneixem la raó, podem calcular el terme general:
$$ a_n = a_1\cdot 0.5^{n-1} $$
Sabem que el producte dels tres primers termes és 1000. Matemàticament,
$$ a_1 \cdot a_2 \cdot a_3 = 1000 $$
Substituïm \(a_1\), \(a_2\) i \(a_3\) de la expressió
anterior pel terme general amb \(n=1\), \(n=2\) i \(n=3\), respectivament:
$$ 1000 = a_1\cdot (a_1 \cdot 0.5)\cdot (a_1\cdot 0.5^2) $$
Amb el que obtenim l'equació
$$ 1000 = a_1 ^3 \cdot 0.5^3$$
Aquesta equació ens proporciona el primer terme:
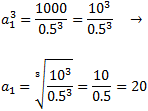
Per tant, la successió és 20, 10, 5,... i la suma dels tres primers termes és 35.
Problema 16
Considereu la successió donada per recurrència
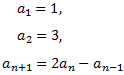
Calcular els termes que siguin necessaris per
poder deduir el seu terme general.
Veure solució
Aplicarem la fórmula donada per calcular, un a un, els primers termes de la successió:
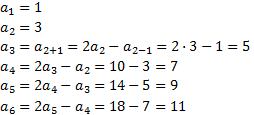
Llavors, la successió és
$$1, 3, 5, 7, 9, 11,...$$
És a dir, és la successió dels nombres imparells.
Per tant, el seu terme general és
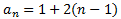
Es tracta d'una successió aritmètica de diferència d = 2.
Nota: al expressar la successió per recurrència, per calcular el terme \(n+1\)-èsim es necessita calcular prèviament tots els termes que li
precedeixen: per calcular \(a_{n+1}\) fan falta
\(a_{n}\) i \(a_{n-1}\) però, per calcular
\(a_{n}\) fan halta \(a_{n-1}\) i \(a_{n-2}\) i, així,
successivament fins arribar a \(a_1\). No ocurreix el mateix si es coneix el terme general.
Problema 17
El sou d'un treballador és de 950€ mensuals i cada any s'incrementa en 50€ (cada mes).
Calcular quants diners guanyarà en els 10 anys següents.
Veure solució
Construïm una successió tal que el terme n-èsim és el sou mensual en el any n-èsim:
En el primer any, el sou mensual és de 950. En el segon any, el sou mensual és de 1000. En el tercero, és de 1050. Llavors, la successió és
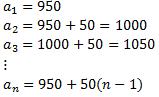
Es tracta d'una seqüència aritmètica amb diferència d = 50.
En total, en l'any n-èsim el sou és 12·an perquè hi ha 12 mesos en un any i cada terme representa el sou
mensual. Per tant, s'ha de multiplicar per 12 la suma
dels 10 primers termes:
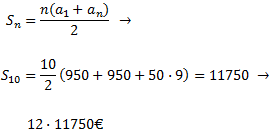
En 10 anys, la xifra ascendeix a 12·11750 = 141000€.
Problema 18
Calcular la suma de tots els nombres imparells compresos entre 100 i 200.
Veure solució
Construimos la seqüència formada per dichos nombres:
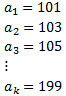
hemos usado k porque no sabem qué posición ocupa l'últim terme. és una seqüència aritmètica amb diferència d = 2 i con terme general
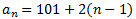
Cerquem la posición de l'últim terme:
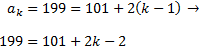
Resolvem l'equació i obtenim k = 50.
Per tant, la suma será
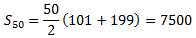
Problema 19
Demostrar que la suma dels n primers nombres imparells és n2.
Veure solució
Considerem la successió dels nombres imparells
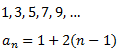
És una successió aritmètica amb diferència d = 2. Volem calcular la suma dels n primers termes, és a dir,
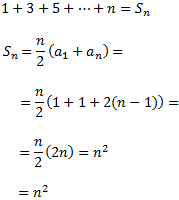
Problema 20
En una seqüència geomètrica, la suma dels dos primers termes és 12 i la suma del primer i del tercero és 30. Trobar el terme general i calcular la suma dels cinc primers termes.
Veure solució
Com que la seqüència és aritmètica, el terme general és
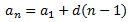
Tenim les dades
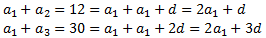
Resolem el sistema d'equacions obtenint el primer terme i la diferència:

Llavors, el terme general és
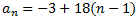
I la suma dels cinc primers és
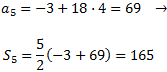
Problema 21
Calcular el valor del paràmetre a perquè els nombres a+2, 3a+2, 9a-2
siguin els tres primers termes d'una progressió geomètrica.
Veure solució
Per a que formen una seqüència geomètrica de raó r s'ha de complir
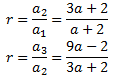
Com que la raó ha de ser constant, igualem ambdues expressions i obtenim el paràmetre a:
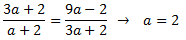
La progressió és
4, 8, 16,…
I té raó r = 2.
Problema 22
En un quadrat de costat 2, s'uneixen els punts mitjos dels seus costats
per obtenir un quadrat inscrit. Es repiteix el procés successivament
amb els quadrats obtinguts:
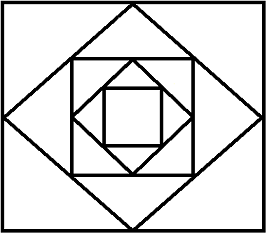
Calcular la successió el terme n-èsim
de la qual es correspon amb la longitud del costat del quadrat n-èsim.
Quin tipus de successió és?
Veure solució
Utilitzarem el teorema de Pitàgores (\(h^2 = a^2+b^2\)) per a calcular els costats.
El costat del quadrat inicial mesura 2.
El costat del primer quadrat mesura
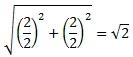
El costat del segon quadrat mesura
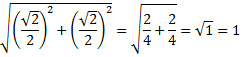
El costat del tercer quadrat mesura
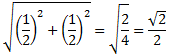
El costat del quart quadrat mesura
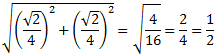
Tenim la successió
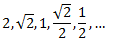
És una successió geomètrica ja que la raó entre termes consecutius es manté constant:
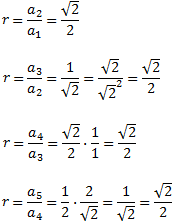
Per tant, el terme general és
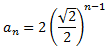
Problema 23
Calcular un nombre sabent que les seves cinc xifres estan
col·locades en forma de seqüència aritmètica, que la suma de les cinc xifres és 20 i que la primera xifra és el doble de la tercera.
Veure solució
Representam el nombre com
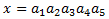
El terme general de la successió que proporciona les cifras és:
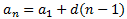
De la suma de totes les xifres i de la rel·lació existent entre la primera i la tercera xifra obtenim les següents equacions:
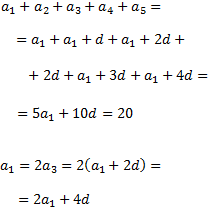
Tenim el sistema d'equacions següent:
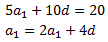
la solució del qual és

La successió és
8,6,4,2,0,…
I, per tant, el nombre cercat és x = 86420.
Problema 24
Calcular la suma dels múltiples de 13 compresos entre els nombres 500 i 7800 (inclosos).
Veure solució
Considerem la progressió aritmètica formada pels múltiples de 13:
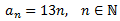
Cerquem el primer terme que sigui major o igual que 500, és a dir,
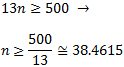
Per tant, el primer múltiple de 13 i major o igual que 500 és
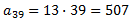
Ara cerquem l'últim múltiple de 13, que de complir
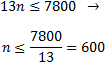
És a dir, és el terme
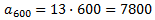
Calculem la suma
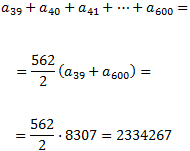
on hem emprat la fórmula de la suma de progressions aritmètiques i 562 és el nombre de termes que hem sumat.
Problema 25
Els dos primers termes d'una seqüència aritmètica
són (a - b)2 i (a + b)2.
Calcular la diferència i la suma dels 5 primers termes.
Veure solució
Com que formen part d'una seqüència aritmètica, si la diferència és d, sabem
que el segon terme és
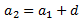
Desenvolupem els quadrats i calculem la diferència d:
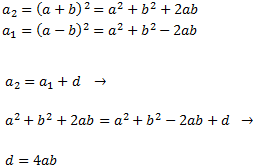
El terme general és
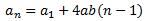
La suma dels 5 primers termes és
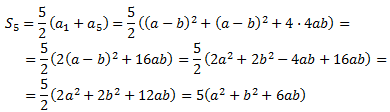
Problema 26
Demostrar que la suma infinita de la successió
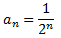
és 1 amb l'ajuda del següent diagrama que representa un quadrat de costat 1.
Veure solució
Calculem els primers termes de la successió:
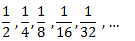
Com que el costat del quadrat és 1, la seua àrea és 1. Llavors, l'àrea de la meitat del quadrat és 1/2. L'àrea de la meitat d'aquesta meitat és 1/4 i, així, successivament:
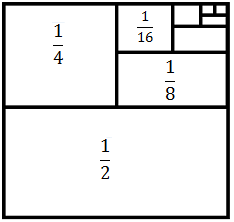
És a dir, les àrees dels quadrats o rectangules que s'obtenen al dividir per la meitat són els termes de la successió. Repetint el procés infinitament, haurem recobert el quadrat per complet (aquest és d'àrea 1). Per tant, la suma de tots els termes de la successió és 1. Així,
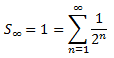
Problema 27
Demostrar que la suma infinita de la seqüència geomètrica
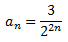
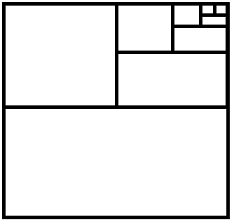
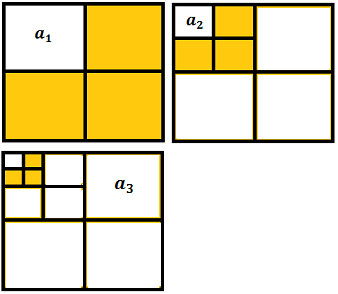
és 1 amb l'ajuda del següent diagrama de quadrats de costat 1
en els que l'àrea groga del n-èsim quadrat val el mateix que el terme n-èsim de la seqüència.
Veure solució
El área total del quadrat és 1. Per tant, l'àrea groga del primer quadrat és
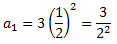
ja que el costat dels quatre quadrats és 1/2.
En el segon quadrat, el costat dels quatre quadrats menuts és la meitat del costat dels quatre quadrats grans, És a dir, 1/4. Per tant, l'àrea groga és
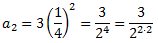
En el tercer quadrat, el costat dels quatre quadrats menuts és la meitat del costat dels quatre quadrats mitjans, és a dir, 1/8. Per tant, l'àrea groga és
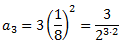
D'aquesta manera, si sumem tots els termes de la successió tindrem l'àrea total del quadrat, que és 1. Així,
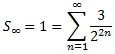
Problema 28
Segons una llegenda, un ric brahman ordenà al seu servent,
Sisa, que pensés un joc per entretenir-se. Sisa
li presentà el tauler d'escacs i el brahmán es quedà tan
satisfet que li permeté escollir la seva recompensa. Axí, Sisa li demanà que li pagués amb un gra de blat pel primer caseller del
tauler, dos grans pel segon, quatre grans pel tercer, huit grans pel
quart, etc. fins arribar als 64 casellers.
Calcular la quantitat de grans de blat que hagué de pagar el brahman.
Veure solució
El nombre de grans en cada casiller correspon amb els termes de la seqüència geomètrica

Volem calcular la suma dels 64 primers termes. Com que la raó és r = 2 i l'últim terme és \(a_{64}\),
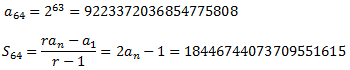
Problema 29
A les 9 del matí, una persona conta a tres amics un secret.
Mitja hora després, cada un dels amics conta el secret
a unes altres tres persones. Mitja hora més tard, cada una d'aquestes persones conta
el secret a unes altres tres persones i, axí, successivament.
Calcular quantes
persones saben el secret a les 9 de la nit suposant que cada persona
conta el secret només a tres persones durant tot el dia i que ninguna persona recibeix la informació varies vegades.
Veure solució
Construïm una successió en la que cada terme será el nombre de persones noves que coneixen el secret:
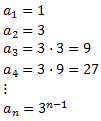
És una successió geomètrica de raó r = 3. Cada mitja hora s'estén el secret i el temps total són 12 hores, és a dir, 24 mitges hores. Aleshores, volem calcular la suma dels 24 primers termes:
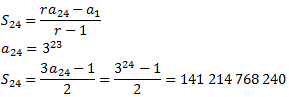
És a dir, el secret el conexeria tothom ja que al món hi ha un poc més de 7.300 milions de persones (xifra del 2015).
Problema 30
Trobar el valor de n perquè es compleixi la igualtat
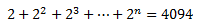
Veure solució
Considerem la seqüència geomètrica de raó 2 i amb primer terme 1. El seu terme general és
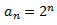
Cerquem n tal que
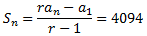
Com que la raó és r = 2,
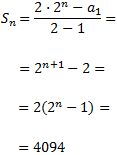
Finalment, resolvem l'equació exponencial