Representación de Gráficas de Funciones
Contenido de esta página:
Introducción y conceptos previos
-
La primera gráfica
-
Gráficas de funciones básicas: función constante, función lineal (recta), función cuadrática, función racional y función a trozo.
Introducción
En esta sección definimos algunos conceptos relativos a las funciones y vemos cómo representar gráficas de funciones básicas (función constante, función recta, función cuadrática, función racional y función a trozos). Además, explicaremos de forma intuitiva el concepto de continuidad de una función.
Antes de todo, debemos recordar la terminología que emplearemos:
Dominio: es el conjunto de sobre el cuál se define la función. Sabemos que una función es como una máquina u operación a la que le damos un número (x) y nos proporciona otro ( f(x) ). El dominio de la función es el conjunto de estas x que le damos a f.
-
Imagen: es el conjunto de los elementos que nos proporciona la función f. Es decir, el conjunto de todos los f(x). En particular, dado un elemento x del dominio, llamamos imagen de x a f(x). Por tanto, la imagen de la función es la imagen del dominio. A la imagen también se le puede llamar codominio.
Gráfica: es la representación de la función. Más concretamente, se define como el conjunto formado por los puntos
(x, f(x)) para todo x del dominio. Más adelante lo veremos más claro.
La primera gráfica
Hemos dicho anteriormente que la gráfica de f es el conjunto de puntos (x, f(x)). Por tanto, si queremos representarla, sólo tenemos que dar valores a x, calcular f(x) y dibujar el punto en el plano. Veamos un ejemplo:
Consideremos la función
$$ f (x) = 2x + 1$$
Escribimos una tabla con los valores que le damos a x (los que queramos) y el valor de su imagen, f(x):
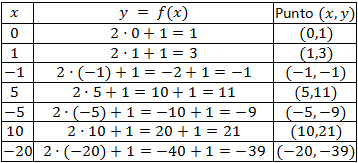
Ahora vamos a representar los puntos. Recordemos que la primera coordenada es la x y la segunda es y = f(x) su imagen
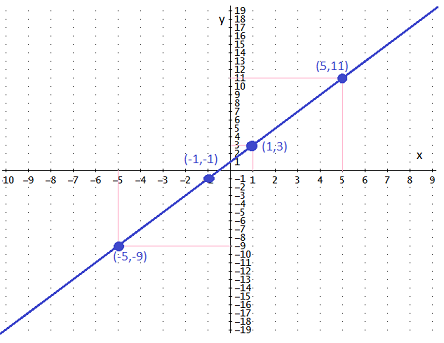
En realidad hemos dibujado sólo 4 puntos y los hemos unido, obteniendo una recta.
Sin embargo, debemos hacernos la siguiente pregunta: ¿cómo sabemos que los puntos forman parte de una recta? ¿no sería posible que la gráfica sea una curva en vez de una recta? Antes de unir los puntos debemos saber de qué tipo de función se trata (una recta, una parábola, una hipérbola, etc. ).
Función constante
Las funciones constantes son las más sencillas, son de la forma
$$f ( x ) = k$$
donde k es un número fijo. Es decir, la función vale lo mismo para cualquier valor de x.
La gráfica de f es una recta paralela al eje OX.
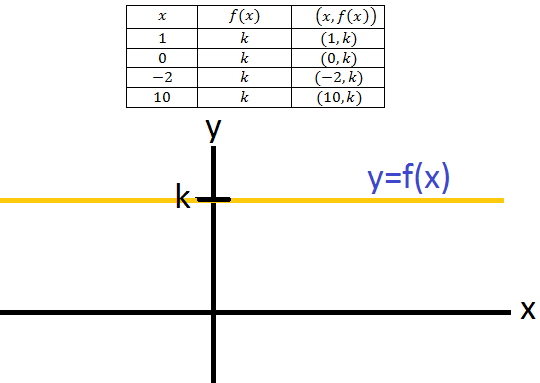
Función recta (o lineal)
Son las funciones de la forma
$$f ( x ) = ax + b$$
donde a y b son constantes. A a se le llama pendiente.
La gráfica es una recta, pero a diferencia de las funciones constantes, la recta puede que no sea horizontal. Es decir, la recta tiene pendiente.
Según los valores de la pendiente, a, la recta será
- a = 0 : la recta es constante, es paralela al eje OX
- a > 0 : la recta es creciente (de izquierda a derecha)
- a < 0 : la recta es decreciente (de izquierda a derecha)
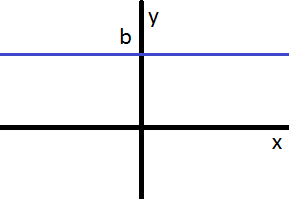
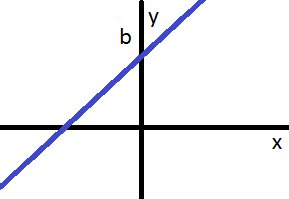
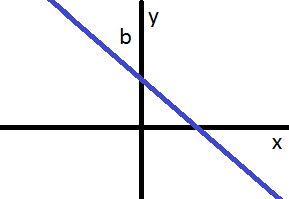
Nota:la gráfica siempre pasa por el punto
$$( 0 , b )$$
Gráfica: será suficiente dibujar dos puntos de la gráfica y unirlos mediante una recta.
Veamos algunos ejemplos (están representadas varias gráficas en los mismo ejes)
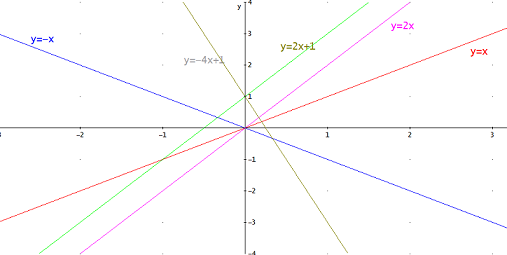
Las gráficas con la misma pendiente (a) y distintos valores para b son rectas paralelas

Puntos de corte con los ejes
$$f ( x ) = ax + b$$
- La recta corta al eje OY cuando x = 0, por tanto, se corta en el punto
$$( 0 , f ( 0 ) ) = ( 0 , b )$$
- Le recta corta al eje OX en el punto x que cumple f ( x ) = 0, es decir, cuando se cumple
$$ 0 = ax + b$$
Calculamos x resolviendo la ecuación:
$$ x = -b / a $$
Luego el punto es
$$( -b / a , 0 )$$
Nota: si a = 0, no corta al eje OX
Función cuadrática
También llamada parábola o de segundo grado.
Son las funciones de la forma
$$f ( x ) = ax^2 + bx + c$$
donde a, b y c son número fijos.
Nota:Debemos exigir que a ≠ 0 ya que si no, sería una recta.
Las parábolas son de la forma

Es decir, el ceficiente director del polinomio, a, nos indica la orientación de la parábola.
Al punto superior de la parábola roja y al inferior de la azul (máximo y mínimo, respectivamente) se les llama vértice de la parábola.
Además, el valor absoluto de a, |a|, influye en el crecimiento (decrecimiento) de la parábola: cuanto mayor sea |a|, más cerrada será la parábola, es decir, más rápidamente crece (o decrece, según el signo de a).
Veamos algunos ejemplos de parábolas (representadas en los mismos ejes)
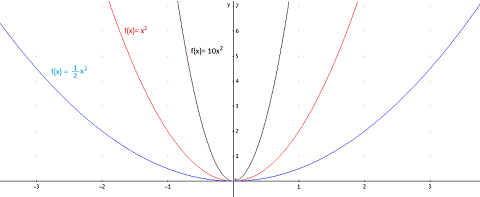
Puntos de corte con los ejes
Las parábolas cortan al eje OY siempre en un único punto. Esto ocurre cuando x = 0, por tanto, el punto es
$$( 0 , f ( 0 ) ) = ( 0 , c )$$
Las parábolas pueden cortan al eje OX en ningúno, uno o dos puntos. Esto ocurre en los puntos x que cumplen
$$f (x ) = 0$$
Es decir, son las soluciones de la ecuación de segundo grado
$$ ax^2 + bx + c = 0$$
que sabemos que tienen una, dos o ninguna solución.
Vértice
Puesto que la forma más rápidda de obtener el vértice analíticamente se necesita cálculo diferencial, directamete diremos que el vértice de la parábola se encuentra en el punto
$$( -b / (2a) , f (-b / (2a)) )$$
Función racional
Son las funciones definidas por una fracción de polinomios.
Por ejemplo
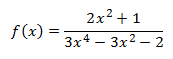
Las principales características de las funciones racionales son
- Su dominio: ya que en éste no puede contener a los valores de x para los que el denominador se anula (no podemos dividir por 0).
- Las asíntotas.
Obtención del dominio
Supongamos que tenemos una función racional
$$ f ( x ) = \frac{N(x)}{D(x)}$$
donde N(x) y D(x) son los polinomios del numerador y denominador, respectivamente.
Para determinar el dominio no es suficiente con excluir los valores para los que el denominador, N, se anula.
Método de obtención del dominio
- Factorizamos los polinomios N y D.
- Simplificamos la función
$$ f ( x ) = \frac{N(x)}{D(x)}$$
usando las factorizaciones de los polinomios (cancelando factores).
- De este modo obtenemos una función racional, expresada en forma de factorizaciones.
- Excluimos del dominio las raíces del polinomio del denominador.
Ejemplo:
Sea la función
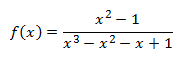
- Factorizamos los polinomios del numerador y del denominador:
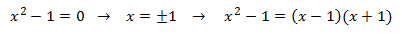
Para factorizar el denominador aplicamos la regla de Ruffini
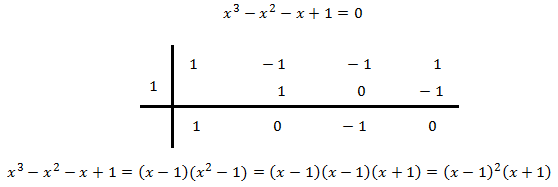
- Expresamos la función como el cociente de las factorizaciones:
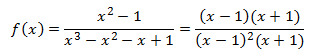
- Simplificamos la expresión anterior:
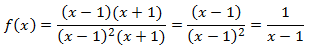
- Excluimos las raíces del polinomio del denominador. Con lo que el dominio es
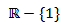
Nota: Si hubiésemos excluido directamente las raíces del polinomio del denominador de la expresión inicial de la función, habríamos obtenido el dominio
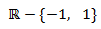
que no corresponde con el dominio real.
Función a trozos
Las funciones definidas a trozos son funciones que están formadas por dos o más funciones. Para cada valor de la variable, se usa una función u otra.
Veamos un ejemplo:
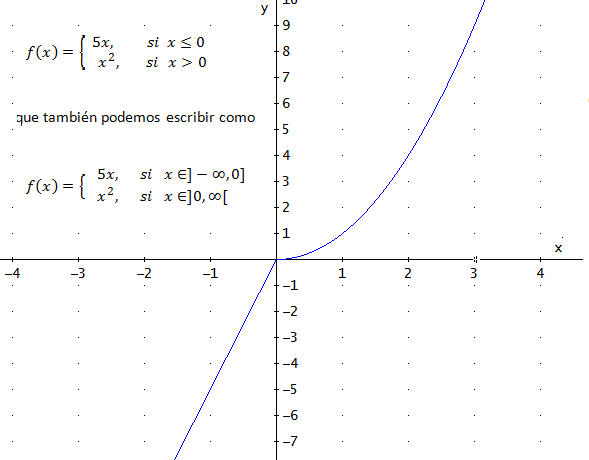
En este ejemplo, la función está definida en dos intervalos: los reales positivos incluyendo al 0 y los reales negativos.
Según el valor de la variable x, escogemos una función u otra.
La función está compuesta por una parábola (en los positivos) y una recta (en los negativos).
En este ejemplo, la función es continua (podemos dibujar la gráfica sin levantar el lápiz del papel). Pero no siempre es asi, como muestra la siguiente función:
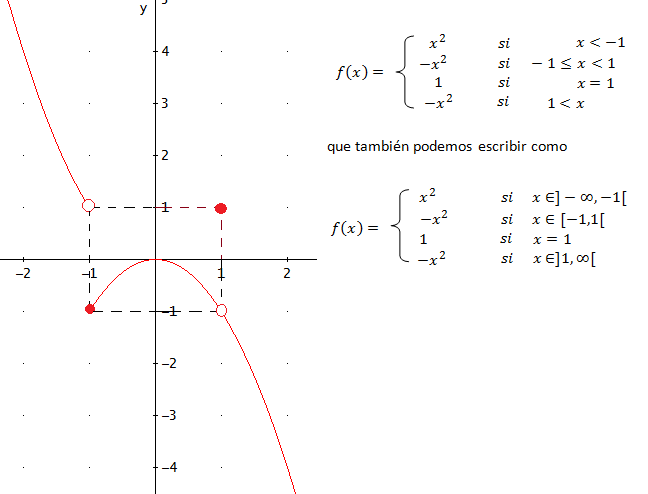
Dibujamos un punto vacío o lleno en los puntos donde cambia la definición de la función (en los extremos de los intervalos y en los puntos aislados) que interpretamos como:
- Si el punto está lleno, significa que es un punto de la gráfica
- Si el punto es vacío, significa que es no es un punto de la gráfica pero que la gráfica se aproxima a él.
En este caso, la función está compuesta por tres parábolas y una función constante (cuando x = 1 ).

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.

