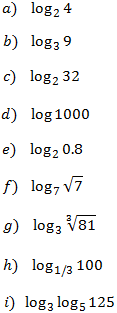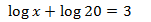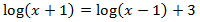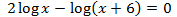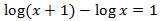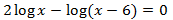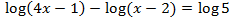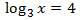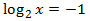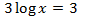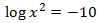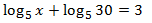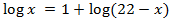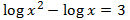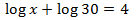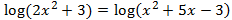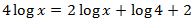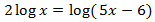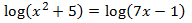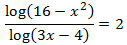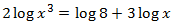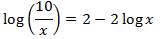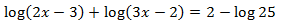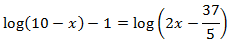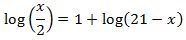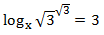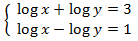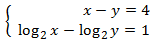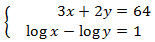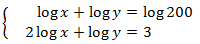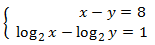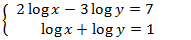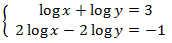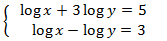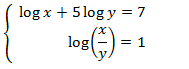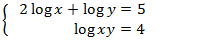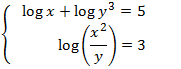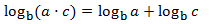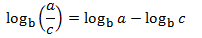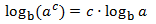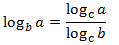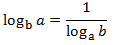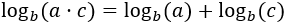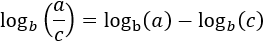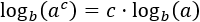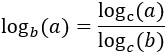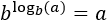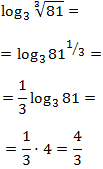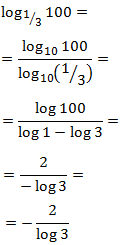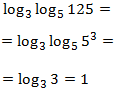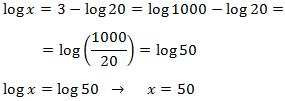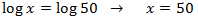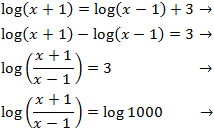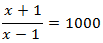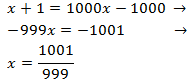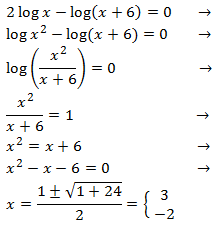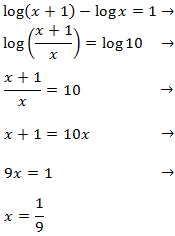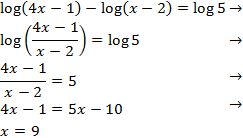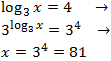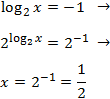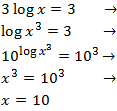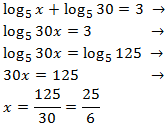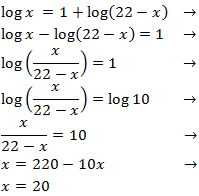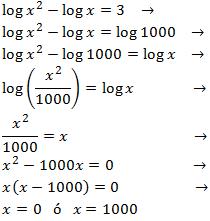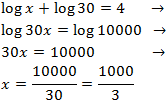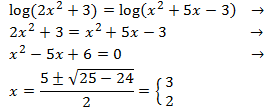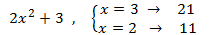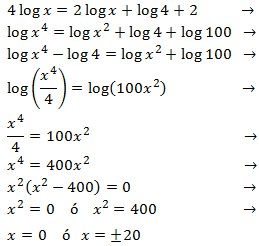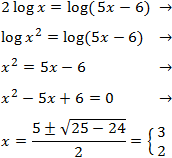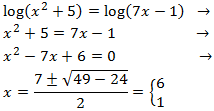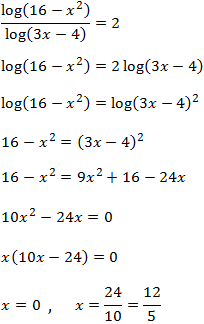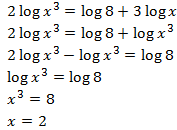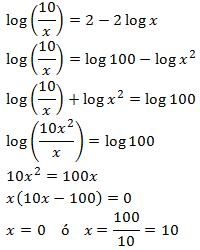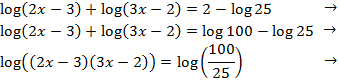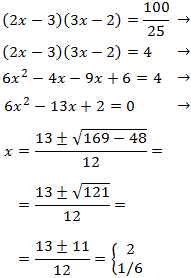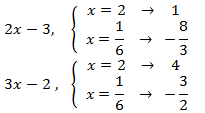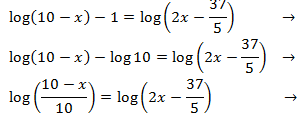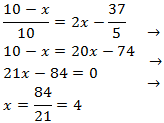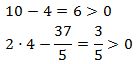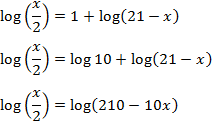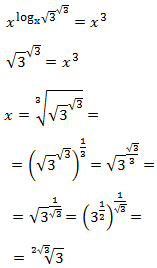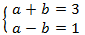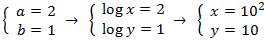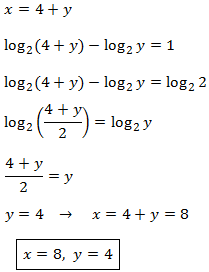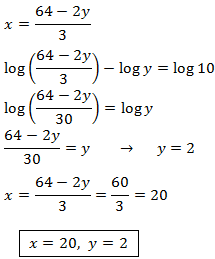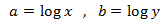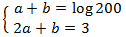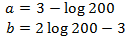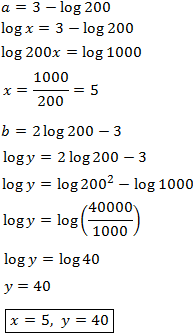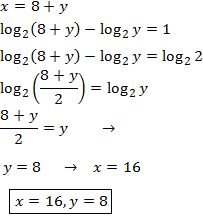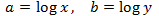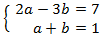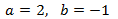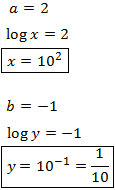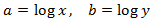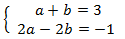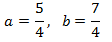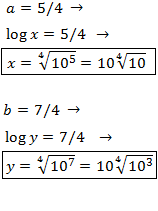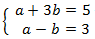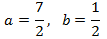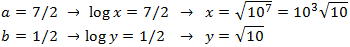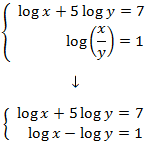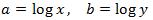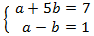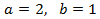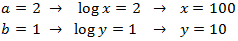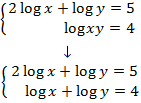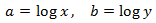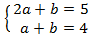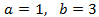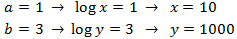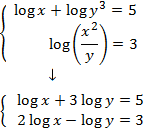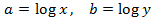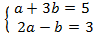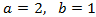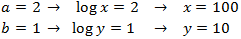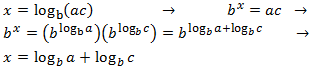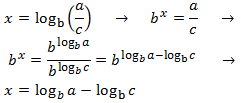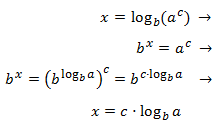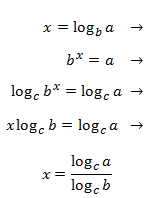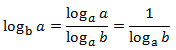Logarithms: Equations, Systems and Properties
|
Content of this page:
-
Introduction
-
Remember that... definition of logarithm and its properties
-
Resolved Logarithmic Equations, Systems and
Demonstration of the properties
Introduction
A logarithmic equation is an equation that has an
unknown factor in the argument of a logarithm.
In reality, the resolution is reduced to the resolution of equations of the same type
as the expressions in the arguments (quadratic equations, cubic equations, irrational equations...).
This section is a collection of resolved
exercises of equations and equation systems of
this kind, which are intended to be in order of increasing difficulty.
In the majority of logarithms the base is not specified, because we suppose it's 10.
Although, in this sense, we must decide that in the majority of scientific texts, if it does not say
otherwise, that the base is e (as it's known, Napierian logarithm).
Also, at the end we will prove the logarithmic properties: logarithm of a product,
of a quotient, of a power and base switch.
Regarding the use of the logarithms, we can
talk of their frequent use in physics.
They appear, for example, to calculate the apparent magnitude
of a celestial body (measured by the amount of light we perceive);
the magnitude of an earthquake in the Richter scale; the age (time gone by)
in radiometric dating (the Carbon 14 test); the pH.
Remember that...
Before starting the exercises, let's remember the definition of logarithm:
$$ log_b (a) = c \Leftrightarrow b^c = a $$
a is called the base of the logarithm
b is called the argument of the logarithm
c the number that
$$ b^c = a $$
So, c is the exponent to which the base b must be raised to be the number a.
$$ b^{log_b (c)} = c $$
- If b is the number e,
we write ln(x) instead loge (x).
This is the
Naperian logarithm.
Logarithm Properties
logarithm of a product:
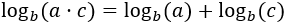
|
logarithm of a quotient:
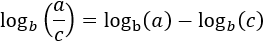
|
logarithm of a power:
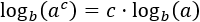
|
change of base:
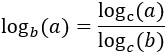
|
Useful property:
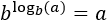
|
Resolved Logarithmic Equations
Exercise 1
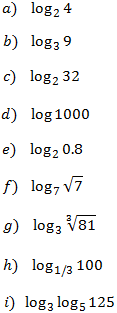
Show solution
-
$$ log_2(4) = $$
$$ =log_2(2^2) = 2 $$
-
$$ log_3(9) = $$
$$ = log_3 (3^2) = 2$$
-
$$ log_2 (32) = $$
$$ = log_2(2^5) = 5 $$
-
$$ log(1000) =$$
$$ = log_{10} (1000)= $$
$$ =log_{10}(10^3) =3 $$
-
$$ log_2(0.8) = $$
$$ =log_2 \left( \frac{8}{10} \right) =$$
$$ = log_2 (8) - log_2(10) = $$
$$ = log_2 (2^3) - log_2(2·5) = $$
$$ = 3 -( log_2 (2·5) ) = $$
$$ = 3 - (log_2(2) + log_2(5))= $$
$$ = 3 - (1+log_2(5)) = $$
$$ = 2 -log_2(5) $$
-
$$ log_7(\sqrt{7}) = log_7(7^{\frac{1}{2}}) = $$
$$ \frac{1}{2} \cdot log_7(7) = $$
$$= \frac{1}{2}\cdot 1 $$
-
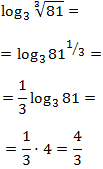
-
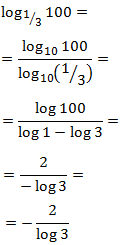
-
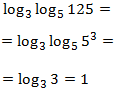
Equation 1
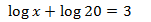
Show solution
We will use the logarithmic properties and that
$$log (1000) = log (10^3) = 3$$
So we can write the equation as
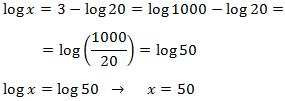
We have an equality between logarithms, so the arguments (what is inside) has to be the same:
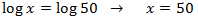
The solution to the equation is x = 50.
Equation 2
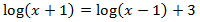
Show solution
We use the logarithmic properties and we write 3 as
$$3=log(10^3)=log(1000)$$
to obtain an equality between logarithms.
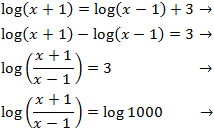
The logarithms are worth the same when their arguments (what's inside) are the same
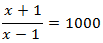
We resolve the equation:
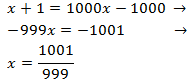
Now we have to prove that for these values of x the arguments are not 0 nor negative.
$$x+1 = \frac{1001}{99} > 0 $$
$$x-1 = \frac{1001}{99}-1 \simeq 0.002 >0 $$
Therefore, it is the solution.
Equation 3
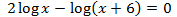
Show solution
In this equation, when applying the properties to obtain an
equality of logarithms, we will need to resolve a quadratic equation:
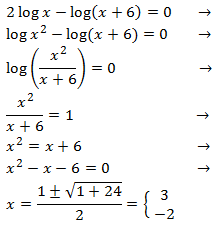
Notice that the only possible solution is x = 3
due to the fact that the arguments have to be positive.
Equation 4
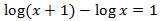
Show solution
We will use that log(10) = 1:
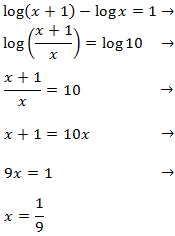
Equation 5
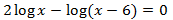
Show solution
$$ 2log(x)-log(x-6)=0 $$
$$ log(x^2) = log(x-6) $$
In order for the logarithms to be the same it is needed that
$$ x^2 = x-6 $$
We solve the quadratic equation:
$$ x^2 -x +6 = 0 $$
$$ x=\frac{1\pm \sqrt{1-24}}{2} $$
Because the discriminant is negative (-23),
there are not any solutions (real ones).
Therefore, there is no solution.
Equation 6
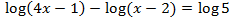
Show solution
Equation 7
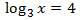
Show solution
As we have two terms that are the same, 3 raised to these terms will be the same number:
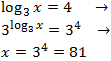
We raise to the power of 3 because 3 is the logarithm's base.
Equation 8
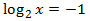
Show solution
Equation 9
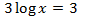
Show solution
Equation 10
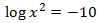
Show solution
We have two terms that are the same, therefore,
if we raise the base, 2,
to these terms we have the same number
$$ 10^{log(x^2)} = 10^{-10} $$
$$ x^2 = 10^{-10} = \frac{1}{10^{10}} $$
Therefore, doing the square root:
$$ x = \pm \sqrt{\frac{1}{10^{10}}} = $$
$$ = \pm \frac{1}{10^5} $$
Because the argument of the logarithm is x squared, both values are solutions
to the equation because when raising to the power of two both numbers are positive.
Equation 11
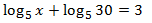
Show solution
We will use that
$$ 3 = log_5(125) $$
Therefore,
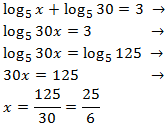
Equation 12
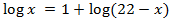
Show solution
We know that
$$ log(10) = 1$$
Therefore,
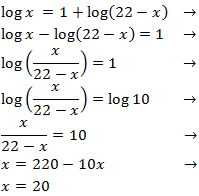
Equation 13
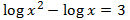
Show solution
We can write 3 like a logarithm:
$$ log(1000) = 3 $$
Therefore,
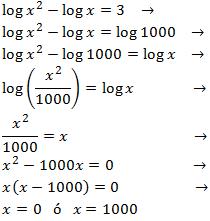
The only solution is x = 1000 due to the fact that the argument of a logarithm can never
be zero.
Equation 14
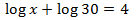
Show solution
We write 4 like a logarithm:
$$ log(10000) = log(10^4) = 4 $$
Therefore
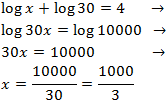
Equation 15
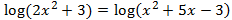
Show solution
We equal the arguments
(what's inside the logarithm) and we resolve the quadratic equation:
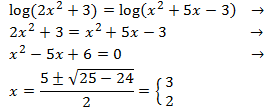
So, the arguments coincide when x = 3 and x = 2, therefore,
the logarithms will be the same. But we have
to prove that for these
values of x the arguments are not 0 nor negative.
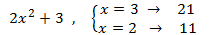
Equation 16
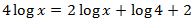
Show solution
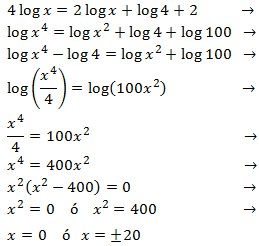
The only possible solution is x = 20, because the argument of
a logarithm has to be necessarily positive.
Equation 17
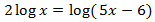
Show solution
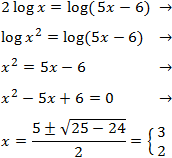
The two square roots of the equation are
solutions to the logarithmic equation because
the two arguments are positive.
Equation 18
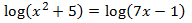
Show solution
Equation 19
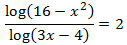
Show solution
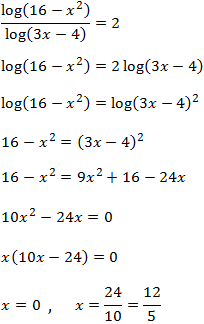
The only solution is
$$ x = \frac{12}{5} $$
because if x = 0, the argument of the denominator's logarithm is negative.
Equation 20
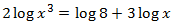
Show solution
Equation 21
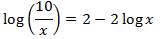
Show solution
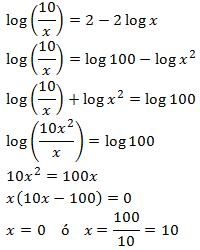
The only solution is x = 10.
Equation 22
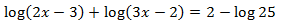
Show solution
We will apply the logarithmic properties and we will write 2 as
$$2 = log (10^2)= log(100)$$
to obtain an equality between logarithms.
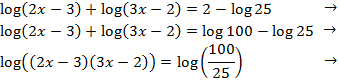
As we already have the equality of logarithms, they will have the same value when they have
the same argument (what's inside), therefore, we obtain a quadratic equation:
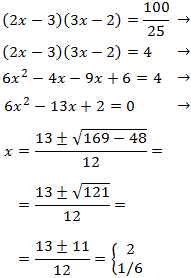
Now we check that for these two (possible) solutions the arguments are positive:
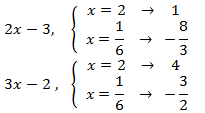
Therefore, the only solution is x = 2.
Equation 23
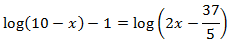
Show solution
We write 1 like \(1 = log(10)\). Therefore,
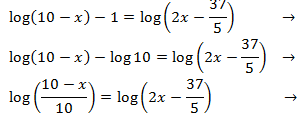
As we have an equality of logarithms (with the same base),
we equal the arguments and resolve the equation:
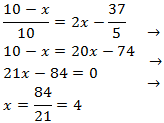
Now we check that the arguments (the polynomials of the logarithms) are positive:
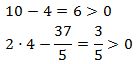
Equation 24
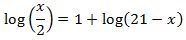
Show solution
Equation 25
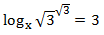
Show solution
In this equation we have the unknown factor x in the base of the logarithm.
What we will do is to use the definition of logarithm,
to calculate it.
In other words, we will use the following property:
$$ log_b (a) = c \Leftrightarrow b^c = a $$
Therefore,
11 Resolved Systems
System 1
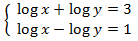
Show solution
We apply the change of variable
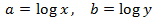
This way we obtain the following linear equation system
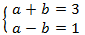
We resolve it and we undo the change of variable:
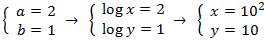
System 2
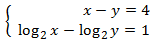
Show solution
Notice that the first equation in the system is not
logarithmic.
We isolate x in the first equation and we substitute in the second:
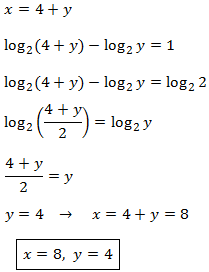
System 3
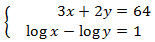
Show solution
This system is similar to the one in the previous exercise:
System 4
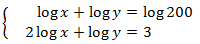
Show solution
We apply a change of variable:
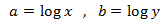
So, we obtain:
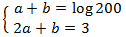
The solution for the previous system is:
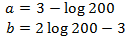
Now we undo the change of variable and we obtain the solutions to the initial system:
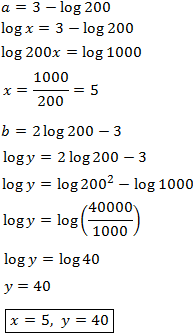
System 5
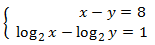
Show solution
We isolate x in the first equation and we substitute in the second:
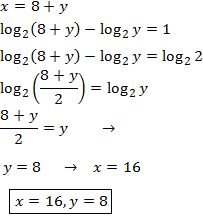
System 6
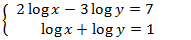
Show solution
We apply the change of variable:
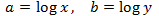
And we obtain the following system:
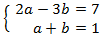
that has as solution:
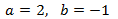
Finally, we undo the change of variable:
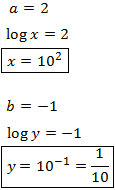
System 7
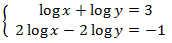
Show solution
We apply a change of variable:
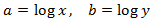
what provides the following system:
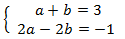
that has as solution:
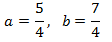
Finally, we undo the change of variable:
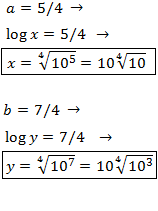
System 8
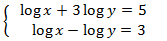
Show solution
We apply the next change of variable:

So we obtain the following system:
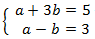
that has as solution:
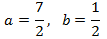
Finally, we undo the change of variable:
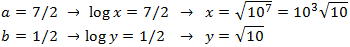
We do not need to check the solutions because they are positive.
System 9
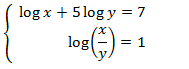
Show solution
First we apply the property logarithm of a product:
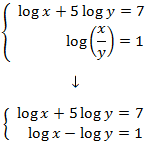
We apply the change of variable:
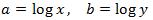
and we obtain the following system:
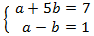
that has as solution:
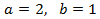
Finally, we undo the change of variable:
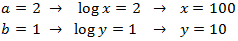
We do not need to check the solutions.
System 10
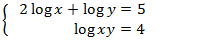
Show solution
We apply the property logarithm of a product:
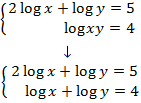
Now we apply a change of variable:
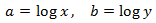
And we obtain the following system:
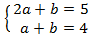
that has as solution
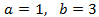
Finally, we undo the change of variable:
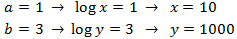
We do not have to check the solutions.
System 11
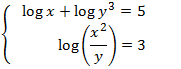
Show solution
We apply the properties logarithm of a quotient and logarithm of a power:
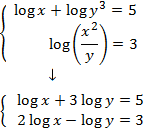
We apply the following change of variable:
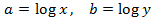
and we obtain the system:
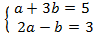
that has as solution
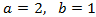
Finally, we undo the change of variable:
Proof of the Properties
Property 1: logarithm of a product
Show Proof
Property 2: logarithm of a quotient
Show Proof
Property 3: logarithm of a power
Show Proof
Property 4: change of base
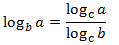
Show Proof
Property 5: change of base
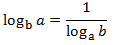
Show Proof

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.