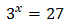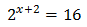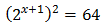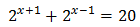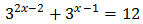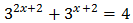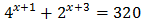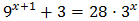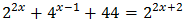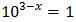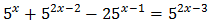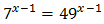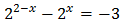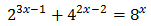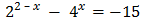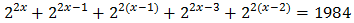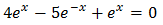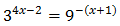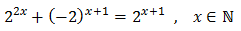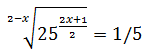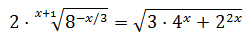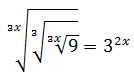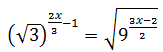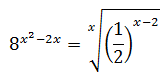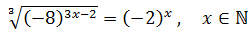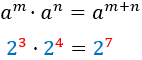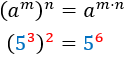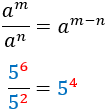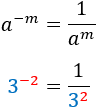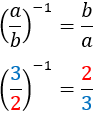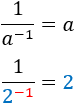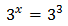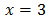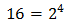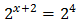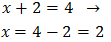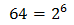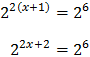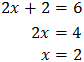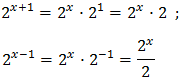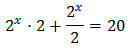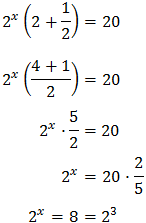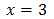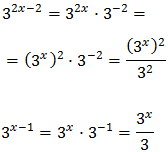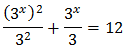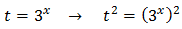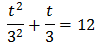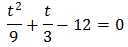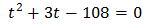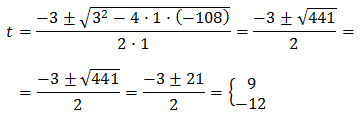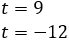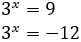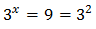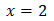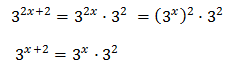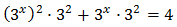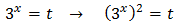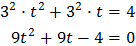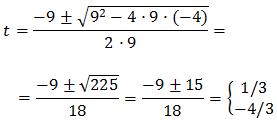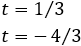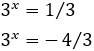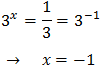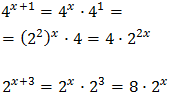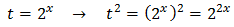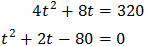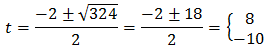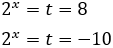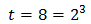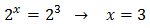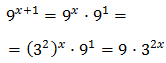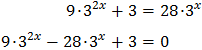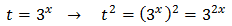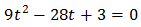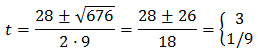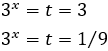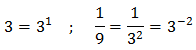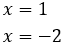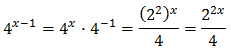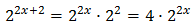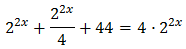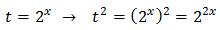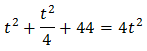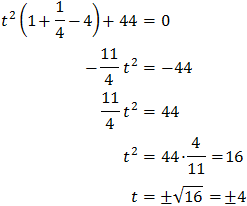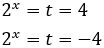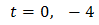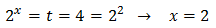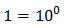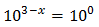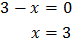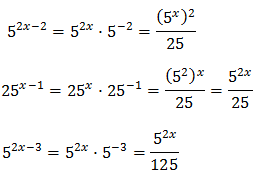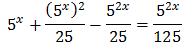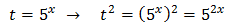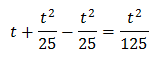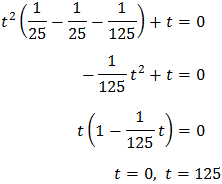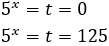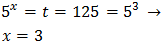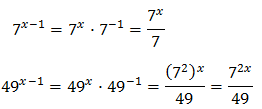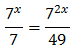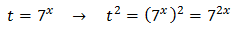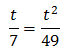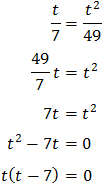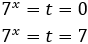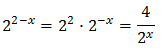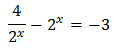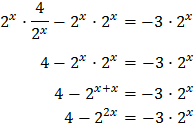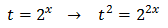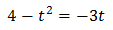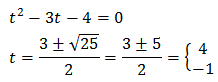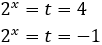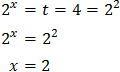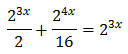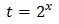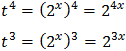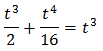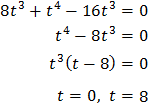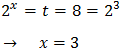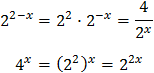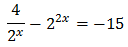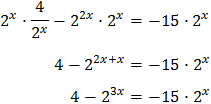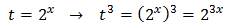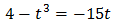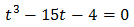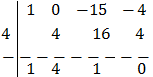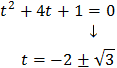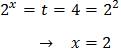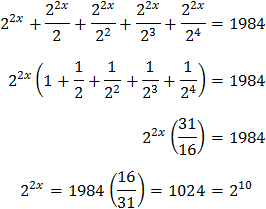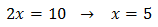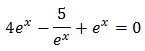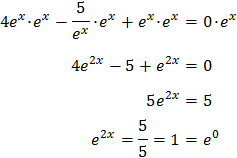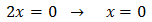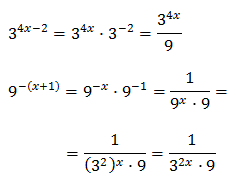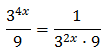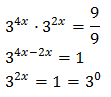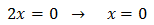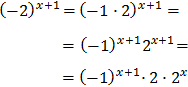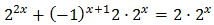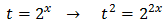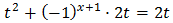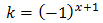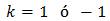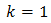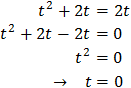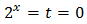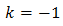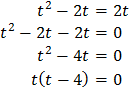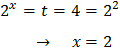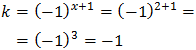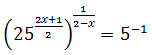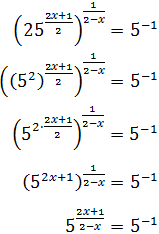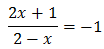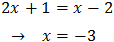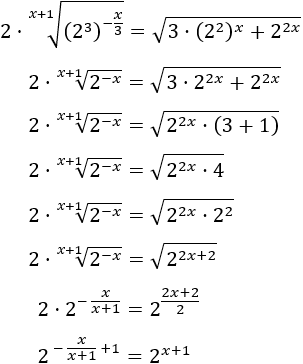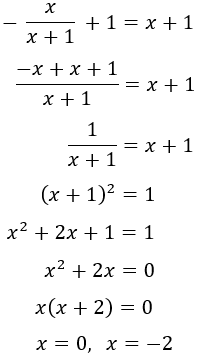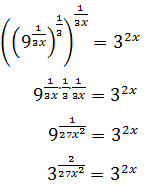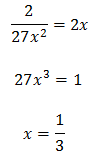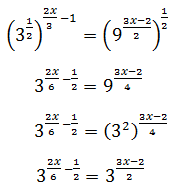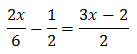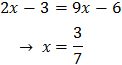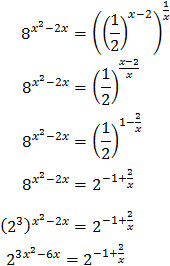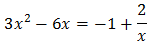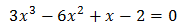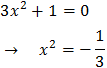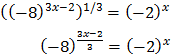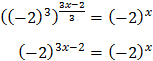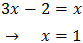Content of this page:
Introduction
An exponential equation is one
that has exponential expressions,
in other words, powers that have in
their exponent expressions with the
unknown factor x.
In this section, we will resolve the
exponential equations without using logarithms.
This method of resolution consists in reaching an equality of the
exponentials with the same base in order to equal the exponents.
For example:
$$ 3^{2x} = 3^6 $$
Obviously, the value that x has to take for the equality to be true is 3.
In order to achieve this type of expressions we have to factorize,
express all the numbers in the form of powers,
apply the properties of powers and write roots as powers.
Sometimes we will need to make a change of variable to transform
the equation in a quadratic one.
We can also resolve using logarithms, but we will leave this type of
procedures for more difficult equations with different bases in the
exponential expressions, making it impossible to use the previous
method of equalizing.
For example,
$$ 3^{x+3} = 5^x $$
which has a real solution, using logarithms of,
$$ x = \frac{3 ln(3)}{ln\left(\frac{5}{3}\right)} $$
Before we start...let's remember the properties of powers
|
Product
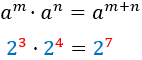
|
Power
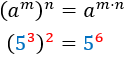
|
| Quotient
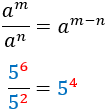
|
Negative exponent
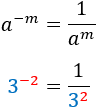
|
| Inverse
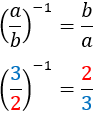
|
Inverse of inverse
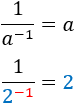
|
Solved Exponential Equations
Equation 1
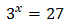
Show solution
Taking into account that
$$ 27=3^2 $$
We can rewrite the equation as
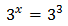
Therefore,
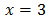
Equation 2
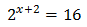
Show solution
Taking into account that
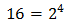
We can rewrite the equation as
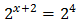
Therefore,
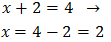
Equation 3
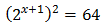
Show solution
Taking into account that
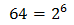
We operate the expression using the properties of powers
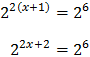
Therefore, we have the linear equation
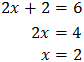
Equation 4
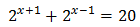
Show solution
Taking into account that
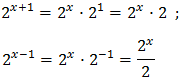
We can rewrite the equation as
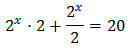
This way, we can extract a common factor of 2 x:
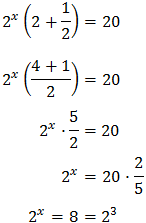
Therefore,
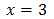
Equation 5
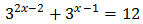
Show solution
Taking into account that
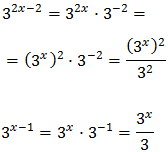
We can rewrite the equation as
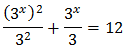
We have the common base 3 x, but because one of them is squared,
we write
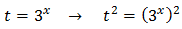
Substituting, the equation finishes like
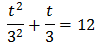
In other words, a quadratic equation:
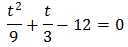
We multiply the full equation by 9:
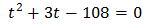
We solve it:
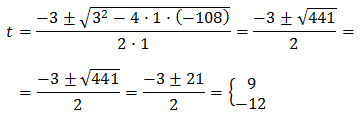
Therefore,
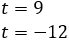
So, we obtain
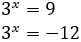
The second option is not possible because it is negative. Therefore,
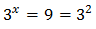
From where we obtain
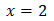
Equation 6
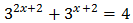
Show solution
Taking into account that
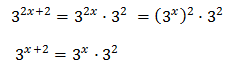
We rewrite the equation as
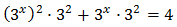
We call t = 3 x:
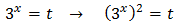
Substituting, the equation finishes like
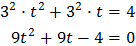
We resolve the quadratic equation:
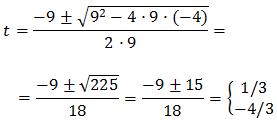
So,
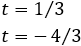
So,
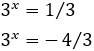
The second solution is not possible because it is negative, but the first one is.
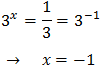
Equation 7
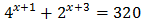
Show solution
Taking into account that
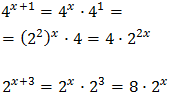
We rewrite the equation as

We call
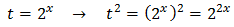
Substituting, the equation finishes like
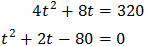
We resolve the previous equation:
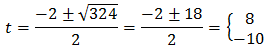
Therefore
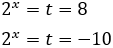
The second option is not possible. So,
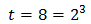
Therefore,
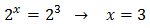
Equation 8
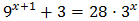
Show solution
Taking into account that
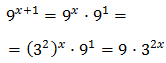
We rewrite the equation as
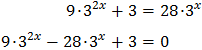
We call
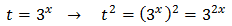
Substituting, the equation finishes like
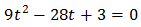
We resolve the quadratic equation:
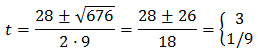
Therefore
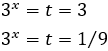
Notice that
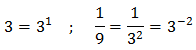
So, both are powers of 3.
Then the two solutions are
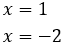
Equation 9
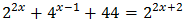
Show solution
Taking into account that
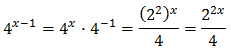
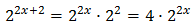
We can rewrite the equation as
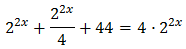
We call
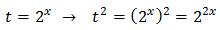
Substituting, the equation finishes like
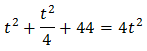
We resolve the equation:
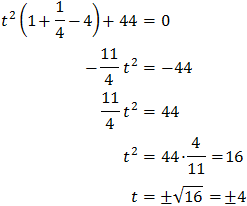
So we have
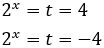
But the solutions
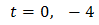
are not possible because one is zero and the other is negative.
So, the only one solution is
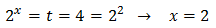
Equation 10
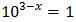
Show solution
Taking into account that
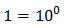
We can rewrite the equation as
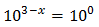
Therefore,
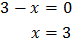
Equation 11
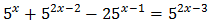
Show solution
Taking into account that
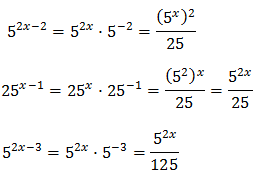
We can rewrite the equation as
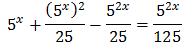
We call
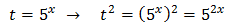
Substituting, we obtain a quadratic equation
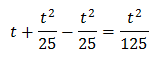
We resolve it:
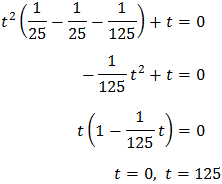
So
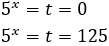
The first solution is not possible because it is zero. Then,
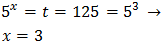
Equation 12
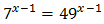
Show solution
Taking into account that
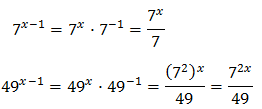
we rewrite the equation as
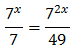
We call
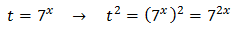
Substituting, we obtain a quadratic equation:
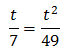
We resolve it:
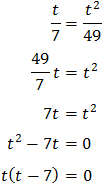
Therefore,
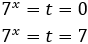
The first solution is not possible because it is zero.
Therefore, the solution is x = 1.
Equation 13
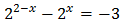
Show solution
Notice that
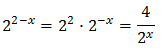
So, the equation can be written as
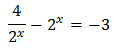
As we have an exponential dividing,
we multiply the full equation by it and that way it disappears:
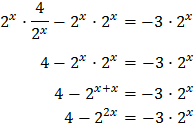
Now we call
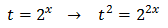
Substituting, the equation finishes like
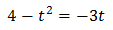
We resolve it:
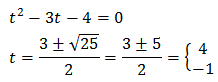
Therefore,
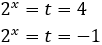
The second solution is not possible because it is negative.
So, the solution is
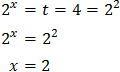
Equation 14
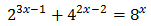
Show solution
Notice that
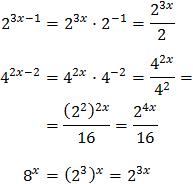
So we write the equation as
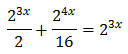
We call
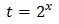
So,
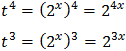
Substituting, we obtain a quartic equation (equation of degree four):
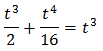
We resolve it:
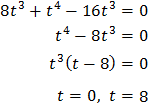
The first solution is not possible because it is zero.
So,
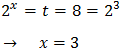
Equation 15
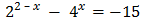
Show solution
Note that
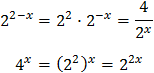
So we can write the equation as
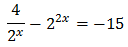
As we have an exponential dividing,
we multiply the full equation by it and that way it disappears:
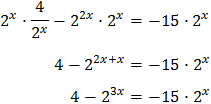
We call
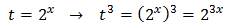
Substituting, we have a cubic equation (degree three)
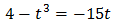
We rewrite it
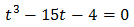
We apply Ruffini's Rule:
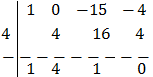
One of the solutions is t = 4.
We calculate the other two:
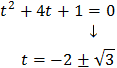
But these are not possible solutions because they are negative.
Therefore,
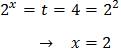
Equation 16
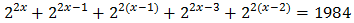
Show solution
We rewrite the equation:
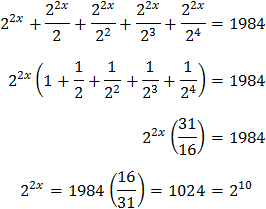
Therefore, the solution is
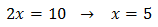
Equation 17
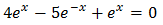
Show solution
We rewrite the equation:
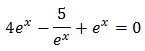
We multiply the full equation by the exponential and that way it disappears:
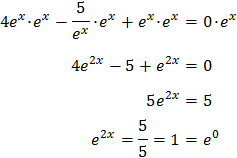
Therefore,
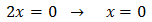
Equation 18
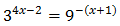
Show solution
Note that
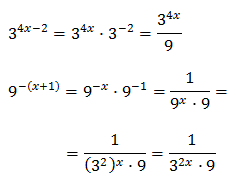
We rewrite the equation:
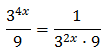
We operate:
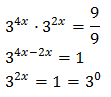
Therefore,
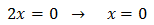
Equation 19
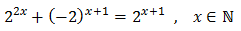
Show solution
Note that
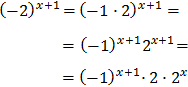
So we rewrite the equation as
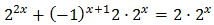
We call
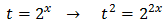
Then we obtain the expression
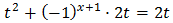
Now we define
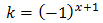
Notice that
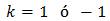
We are going to suppose that
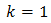
Therefore
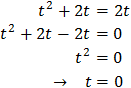
So
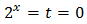
And this is not possible.
So, let's suppose
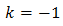
Therefore,
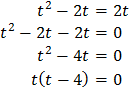
One solution would be t = 0 but, like before, is not possible.
The other solution is
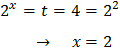
But we have supposed that k = -1 and we have to check that it is true:
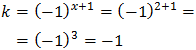
Because it's true, the solution to the equation is x = 2.
Equation 20
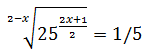
Show solution
We rewrite the equation as
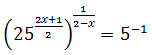
We use 25 = 52 and the properties
of powers (we write the root in the form of a power):
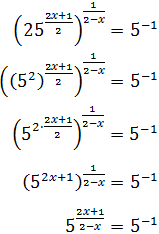
The, we have
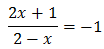
Finally, we resolve the equation:
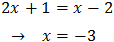
Equation 21
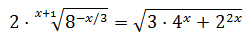
Show solution
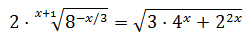
We write the roots in the form of powers
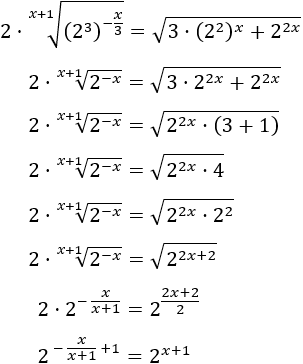
We want for this to be true:
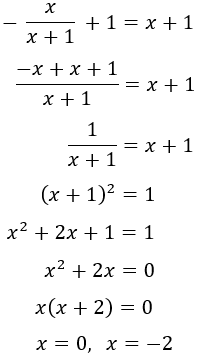
Therefore, we have two solutions:
$$ x = 0,\ x = -2 $$
Equation 22
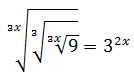
Show solution
We have three nested roots (one inside the other).
We write the roots in the form of powers.
The equations ends up like
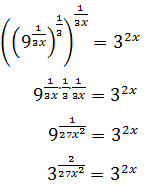
We resolve the equation and we obtain the solution
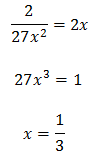
Equation 23
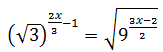
Show solution
We write the roots in the form of powers:
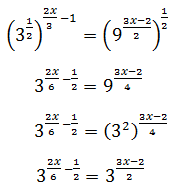
We want for this to be true:
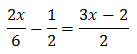
Finally, we resolve the linear equation:
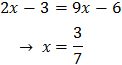
Equation 24
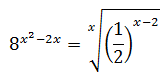
Show solution
We write the root in the form of powers:
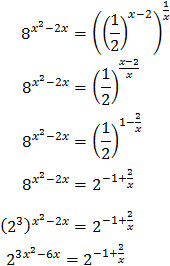
We want this to be true:
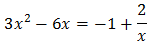
Taking into account that x cannot be 0.
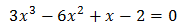
We apply Ruffini's Rule:

One solution is x = 2. We calculate the others:
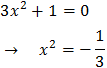
There aren't any real solutions.
Therefore, the only solution to the exponential equation is
$$ x = 2 $$
Equation 25
Show solution
We write the roots in the form of powers.
The equation ends up like:
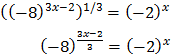
Note that -8 = (-2)3
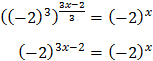
We want this to be true:
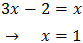

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.