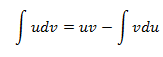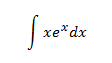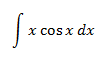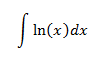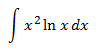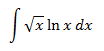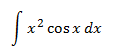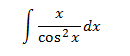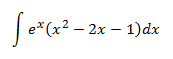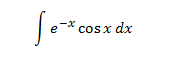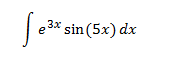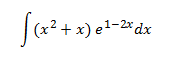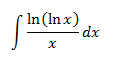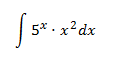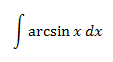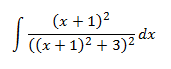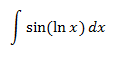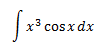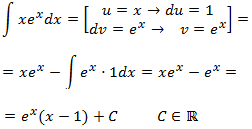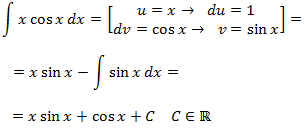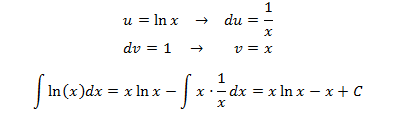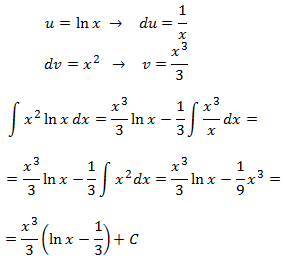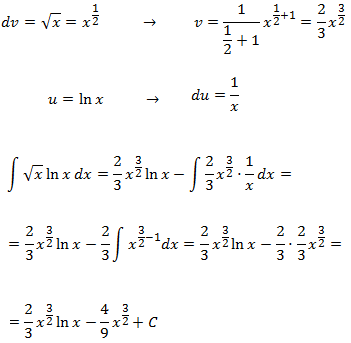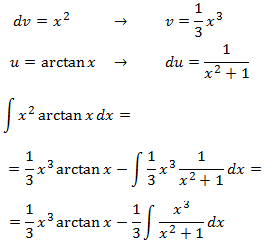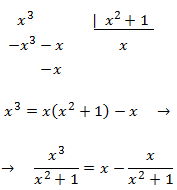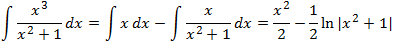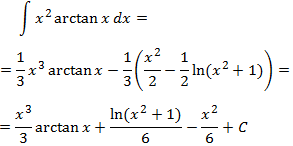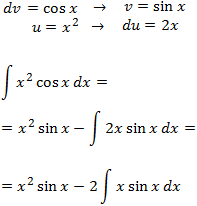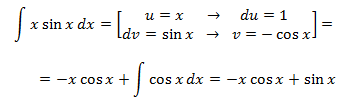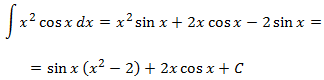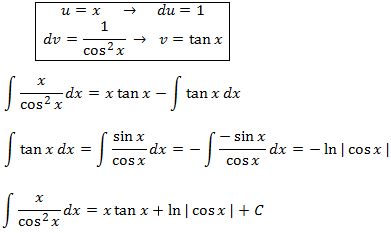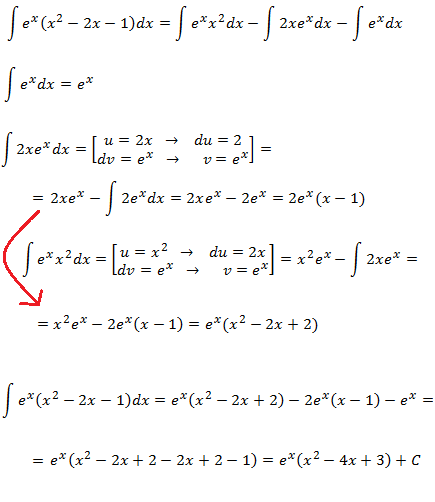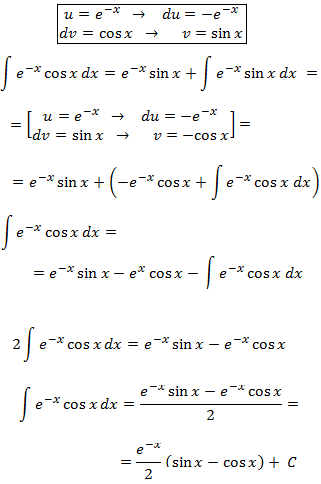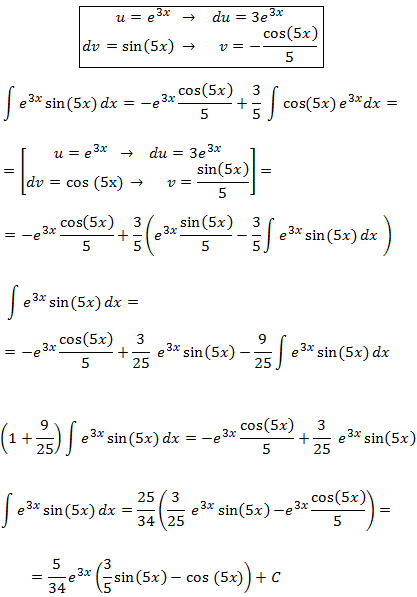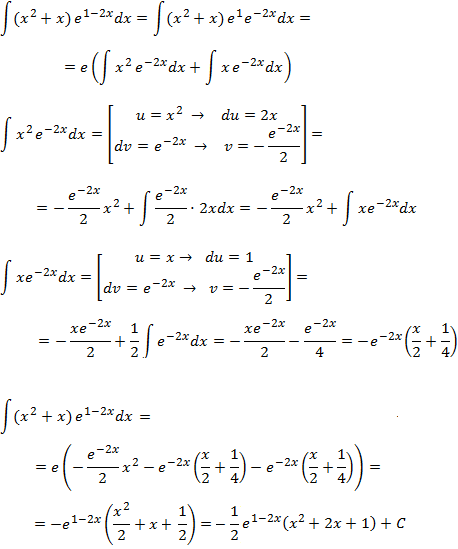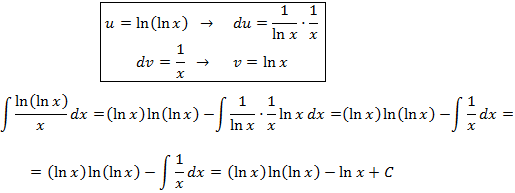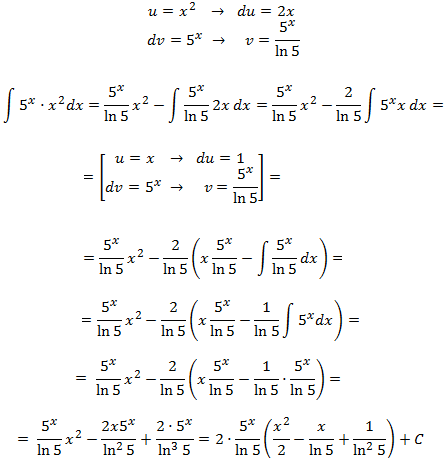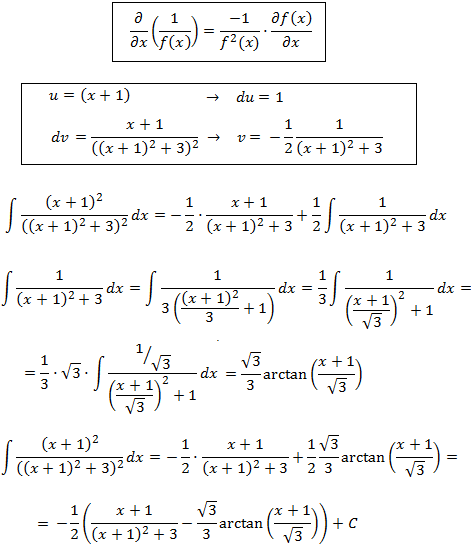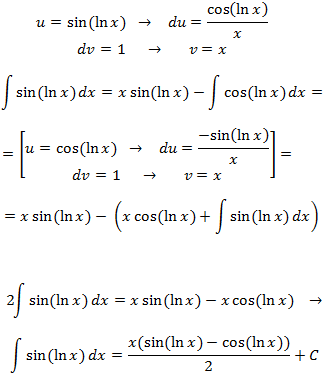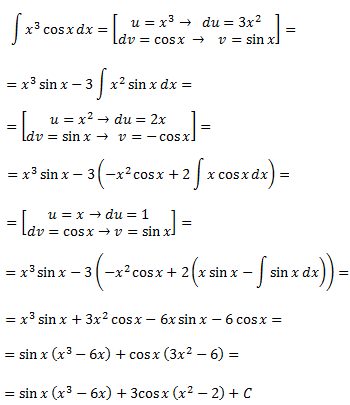Content of this page:
Introduction
When the integrand is formed by a product (or a division, which we can treat like a product)
it's recommended the use of the method known as integration by parts,
that consists in applying the following formula:
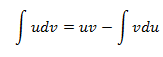
Even though it's a simple formula, it has to be applied correctly.
Let's see a few tips on how to apply it well:
Select u and dv correctly: A bad choice can
complicate the integrand. Supposing we have a product, and one of the factors is monomial
(x3 for example). If we consider that dv = x3, then
by using integration we obtain that
$$ v = \frac{x^4}{4} $$
We have increased the exponent and this could mean a step back in the process.
Something similar happens with fractions (like 1/x). If we take dv = 1/x,
we will obtain v = log|x|, and probably end up with a harder integration process.
As a rule, we will call u all powers and logarithms; and dv exponentials,
fractions and trigonometric functions (circular functions).
-
Don't change our minds about the selection: Sometimes we need to
apply the method more than once for the same integral.
When this happens, we need to call u the result of du from the
first integral we applied the method to.
The same applies to dv. If we don't do this, seeing as choosing one option
or another involves integration or differentiating,
we'll be undoing the previous step and we won't be able to advance.
-
Cyclic integrals: Sometimes, after applying integration
by parts twice we have to isolate the very integral
from the equality we've obtained in order to resolve it.
An example of this is exercise 10.
Integrals solved step by step
Integral 1
Show solution
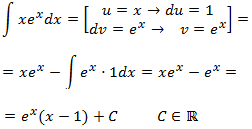
Notes: it's important to choose
$$ x = u \rightarrow dx = du$$
because by doing so we're reducing the monomials degree (from 1 to 0). If we choose
$$ x = dv \rightarrow v = \frac{x^2}{2} $$
we increase the degree (from 1 to 2) and we complicate
the integral more because the exponential factor remains the same and we're
left with this integral
$$ \int {\frac{x^2}{2}\cdot e^x }dx$$
Integral 2
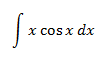
Show solution
Notes: As seen in the exercise before,
it doesn't matter if cos(x) in u or dv
(due to the fact we obtain a sinus). We choose u = x to
reduce it's degree (and that way x disappears). If we choose dv = x,
we increase the degree.
$$ dv = x \rightarrow v = \frac{x^2}{2}$$
Integral 3
Show solution
In this integral we don't have an explicit product of functions,
but we don't know what the logarithms primitive function is, so we differentiate it,
that way u = ln(x).
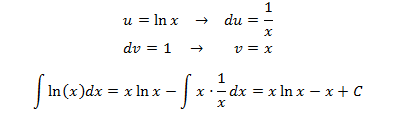
Integral 4
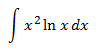
Show solution
It's in our interest to select u = x2 (to reduce the exponent)
but then we're forced that dv = ln(x) and obtaining v isn't immediate.
So we'll select the other case
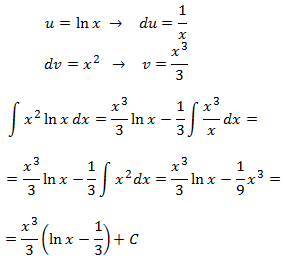
Integral 5
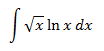
Show solution
If we chose dv = ln(x), we won't be able to obtain v easily.
It's better to chose u = ln(x)
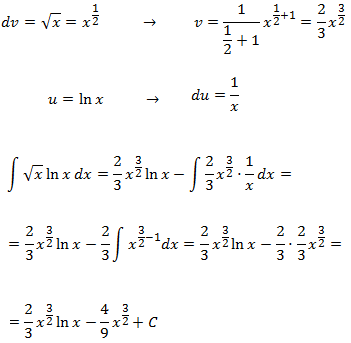
Integral 6

Show solution
Usually, we would select u = x2 to reduce the exponent,
but then we would end up with dv = arctan(x) and we don't know the primitive
of arctan. So we will select
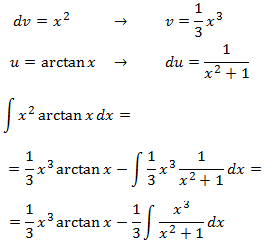
Now we have to calculate the integral of a rational function. In order to
simplify the expression we're going to divide the polynomials:
$$\frac{P(x)}{Q(x)} \rightarrow P(x) = Q(x)C(x) + R(x) $$
where C(x) is the quotient and R(x) is the remainder.
Dividing the expression by Q(x) we get
$$ \frac{P(x)}{Q(x)} = C(x)+ \frac{R(x)}{Q(x)}$$
We'll use this break down in the integral:
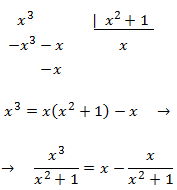
We resolve the integral:
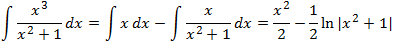
Then
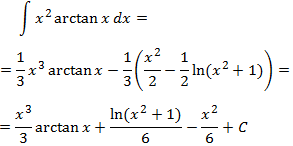
Note: We have taken the absolute value away
from the logarithm because it always has a positive argument.
Integral 7
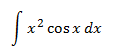
Show solution
Every time we integrate or differentiate cos(x) we obtain
±sin(x). So, it doesn't matter if it's u or dv. However,
it's
better to choose u = x2 because when we differentiate we reduce the
exponent: du = 2x. We will select dv = cos(x).
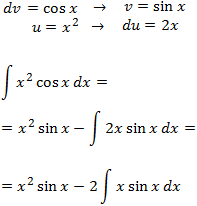
We integrate by
parts again, but we have
to chose u = x, if not we return to the previous step:
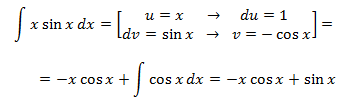
Then,
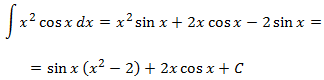
Integral 8
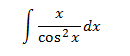
Show solution
We choose u = x to reduce its exponent (and that way x disappears).
The primitive of
$$ \frac{1}{cos^2(x)}$$
is immediate:
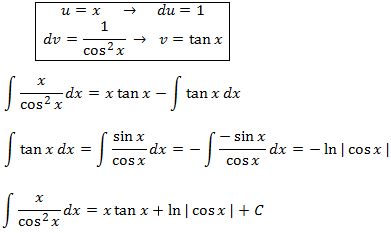
Integral 9
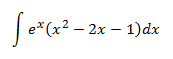
Show solution
Similar to what happens with sin(x) and cos(x), when we
differentiate or integrate ex we obtain ex, so
it's indifferent whether it's u or dv. If we select the
exponential to be u, this factor
will always stay in the integral and furthermore the monomial (power) will be dv,
and we will increase its degree when calculating v. So we'll select
dv = ex and the monomials of the
polynomial as u to reduce the exponent until it's a constant.
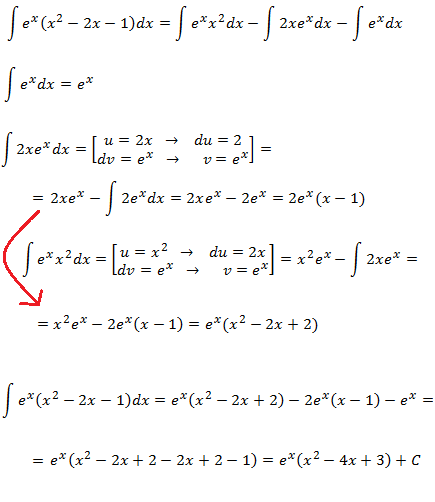
Integral 10
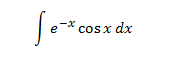
Show solution
In this example it doesn't matter which factors
are u and dv, because when integrating and differentiating
e -x we obtain –e -x and when
integrating and differentiating cos(x)
we get ±sin(x). This is a cyclical integral in which we have to
apply integration by parts twice (with the same choices so
we don't go backwards) and we have to isolate
the integral from the mathematical expression we obtain.
Integral 11
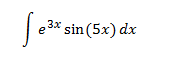
Show solution
We have a exponential multiplied by sine once again, so we
are up against a cyclic integration because we must apply the
integration by parts process twice(always with the same
selection so we don't go back a step) and isolate the integral from the
expression we obtain.
We can chose u and dv as we please.
Integral 12
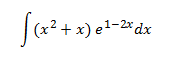
Show solution
We choose the polynomial as u to reduce the exponents until they disappear.
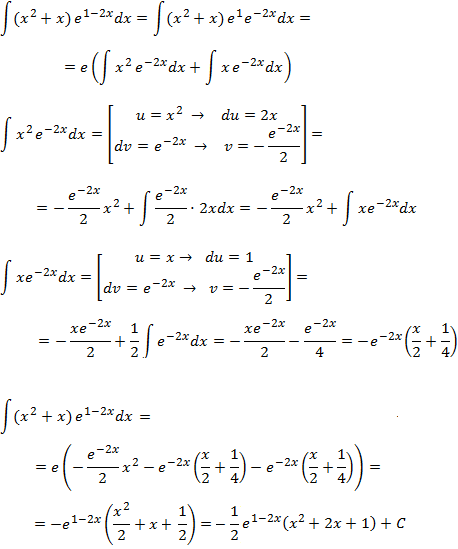
Integral 13
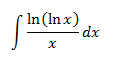
Show solution
Integral 14
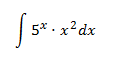
Show solution
Each time we differentiate or integrate exponentials
we obtain the same exponential but multiplied by a constant
(or the inverse of said constant), so which is u or dv doesn't matter.
We select in function of the other factor
and seeing it's a monomial we make u = x2 to reduce the exponent:
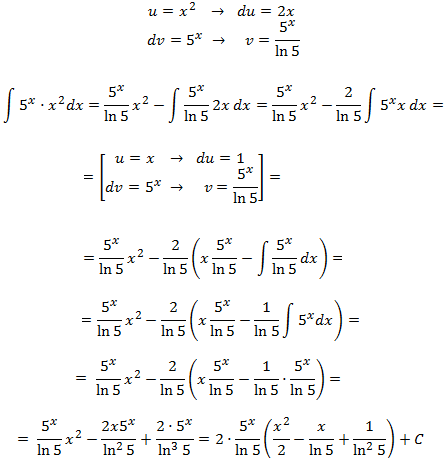
Integral 15
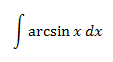
Show solution
The integral of arcsine can be considered direct, but we can
also calculate its primitive using integration by parts:

Integral 16
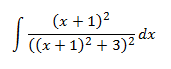
Show solution
Integral 17
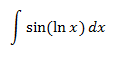
Show solution
This is a cyclical integral in which we have to
apply integration by parts twice (with the same choices):
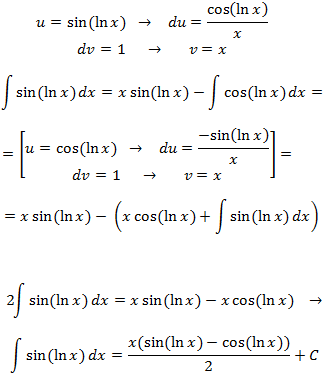
Integral 18
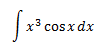
Show solution
We have to
apply integration by parts three times (with the same choices):
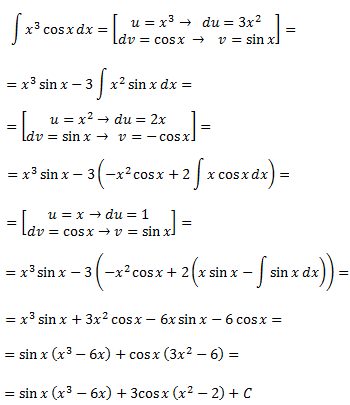

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.