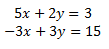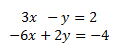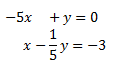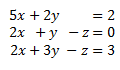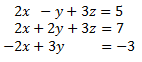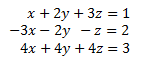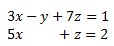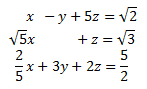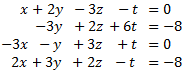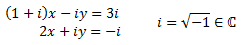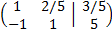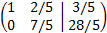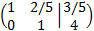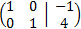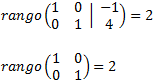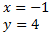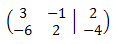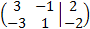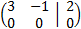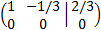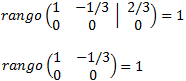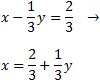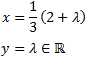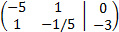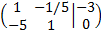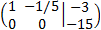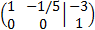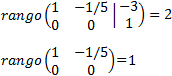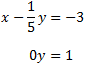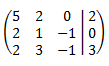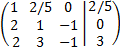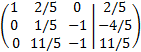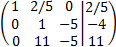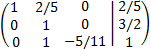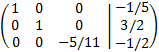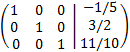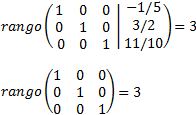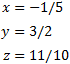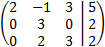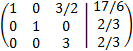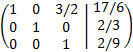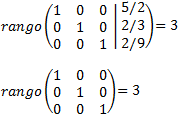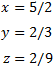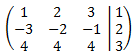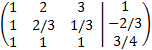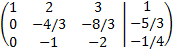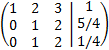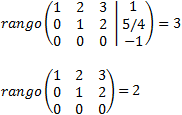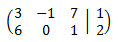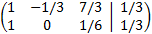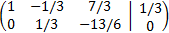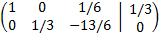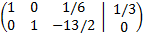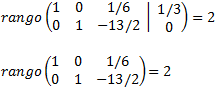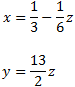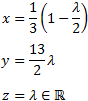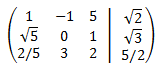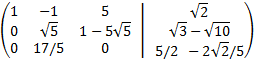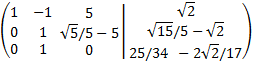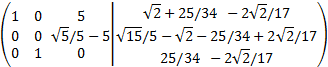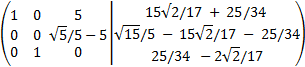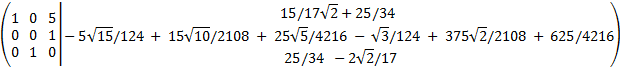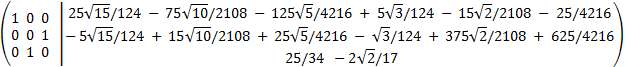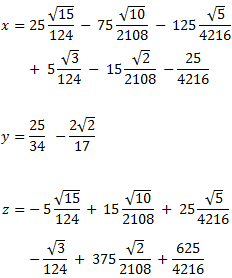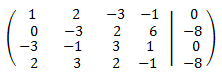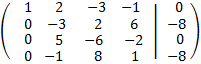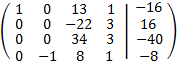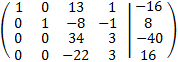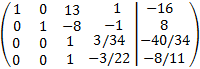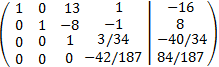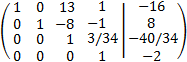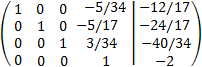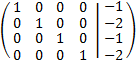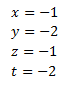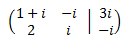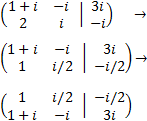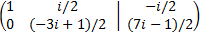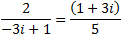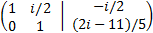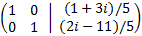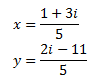Content of this page:
Introduction
A system of equations (linear) is a group of (linear) equations with
various unknown factors. Generally speaking, the unknown factors appear in various equations.
What an equation with various unknown factors does is relates them amongst each other.
Solving a system consists in finding the value for the unknown factors in a way that verifies
all the equations that make up the system.
-
If there is a single solution (one value for each unknown factor) we will say that the
system is Consistent Independent System (CIS).
-
If there are various solutions (the system has infinitely many solutions), we say that the system is a
Consistent Dependent System (CDS). .
-
If there is no solution, and this will happen if there are two
or more equations that can't be verified at the same time,
we say it's an Inconsistent System (IS). For example,
the following system of equations
$$ \begin{cases} \begin{array}{lcl} y & = & 0 \\ 2x + y & = & 0 \\ 2x + y & = & 2 \end{array} \end{cases}$$
is inconsistent because of we obtain the solution x = 0 from the second equation and, from the third, x = 1.
In this section we are going to solve systems using the Gaussian Elimination method, which consists in simply doing elemental operations in row or column of the augmented matrix to
obtain its echelon form or its reduced echelon
form (Gauss-Jordan).
Resolution Method
We apply the Gauss-Jordan Elimination method: we obtain the
reduced row echelon form from the augmented matrix of
the equation system by performing elemental operations in rows (or columns).
Once we have the matrix, we apply the Rouché-Capelli theorem to determine
the type of system and to obtain the solution(s), that are as:
Let A·X = B be a system of m linear equations with n unknown
factors, m and n being natural numbers (not zero):
AX = B is consistent if, and only if,
$$ rank(A)=rank(A|B) $$
AX = B is consistent independent if, and only if,
$$ rank(A)=n=rank(A|B) $$
Note: The elemental operations in rows or columns allow us to obtain equivalent systems to the initial one, but with a form that simplifies obtaining the solutions (if there are). Also, there are quicker
tools to work out the solutions in the CIS, like Cramer's rule.
Solved Systems
System 1
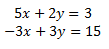
Show Solution
The augmented matrix of the system is

of the same dimension as the system (2x3).
The vertical line that separates the matrix coefficients from the vector of the independent terms.
We perform elemental operations in the rows to obtain the reduced row echelon form:
We multiply the first row by 1/5 and the second by 1/3
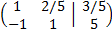
We add the second row with the first
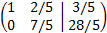
We multiply the second row by 5/7
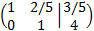
We add the first row with the second one multiplied by -2/5
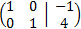
This last equivalent matrix is in the reduced row echelon form
and it allows us to quickly see the rank of
the coefficient matrix and the augmented one.
We calculate the ranks:
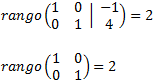
By the Rouché-Capelli theorem, the system is consistent Independent. The matrix we have obtained represents the system
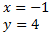
which is the solution to the initial system.
System 2
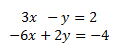
Show Solution
The augmented matrix of the system is
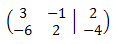
We perform elemental operations in the rows to obtain the reduced
row echelon form:
We multiply the second row by 1/2
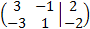
We add the first row with the second
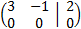
We multiply the first row by 1/3
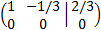
This last equivalent matrix is in the reduced row echelon form and it has a null row, which means that the rows in the initial system are linearly dependent
(either one of them can be obtained by another multiplying it by a scalar that is not null).
We calculate the ranks
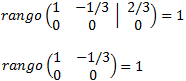
By the Rouché-Capelli theorem, the system is consistent. Further, it is dependent, because of the rank (1) is lower than the number of unknown factors (2).
The matrix we have obtained represents the system
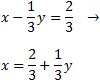
The solutions are
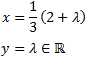
System 3
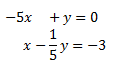
Show Solution
The augmented matrix of the system is
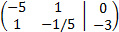
We perform elemental operations in the rows to obtain the reduced row echelon form
We change the order of the rows (this way we will already have a 1 in the first row without any need to multiply)
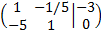
We add the second row with the first one multiplied by 5:
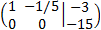
We multiply the second row by -1/15
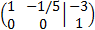
This last matrix is in the echelon form (not reduced).
We can directly observe that the system is inconsistent because we have
the following equality (second row):
$$0x + 0y = 1$$
that is an impossible equality.
We calculate the ranks of the coefficient matrix and the augmented one:
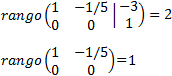
By the Rouché-Capelli theorem, the system is inconsistent (there is no solution).
The matrix we have obtained represents the system
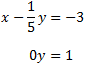
The system is inconsistent because we have the impossible equality
$$ 0 = 1 $$
System 4
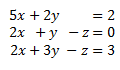
Show Solution
The augmented matrix of the system is
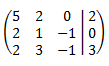
(dimension 3x4).
We perform elemental operations in the rows to obtain the reduced row echelon form
We multiply the first row by 1/5
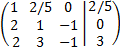
We add the second and third rows with the first one multiplied by -2
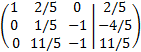
We multiply the second and third rows by 5
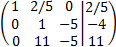
We add the second row with the third one multiplied by -1

We multiply the second row by -1/10 and the third one by 1/11
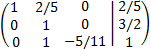
We add the first row with the second one multiplied by -2/5 and the third with the second one multiplied by -1
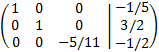
We multiply the third row by -11/5
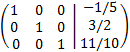
This last equivalent matrix is in the reduced row echelon form (we know it because it is the identity matrix).
By having the identity matrix, we know that it is a consistent independent system and we can obtain the single solution.
We calculate the ranks
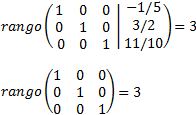
By the Rouché-Capelli theorem, the system is consistent Independent. The matrix we have obtained represents the system
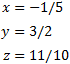
which is the solution to the system.
System 5
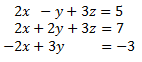
Show Solution
The augmented matrix of the system is

We perform elemental operations in the rows to obtain the reduced row echelon form
We subtract the first row to the second one and we add the third row with the first.
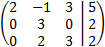
We multiply the first row by 1/2 and the second one by 1/3

We add the first row with the second one multiplied by 1/2 and the third row with the second one multiplied by -2
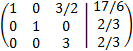
We multiply the third row by 1/3
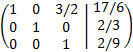
We add the first row with the third multiplied by -3/2

This last matrix is a row reduced echelon matrix (we know this because we have the identity matrix).
We calculate the ranks
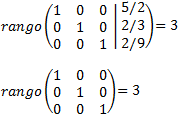
By the Rouché-Capelli theorem, the system is consistent Independent. The matrix we have obtained represents the system
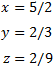
System 6
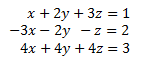
Show Solution
The augmented matrix of the system is
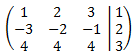
We perform elemental operations in the rows to obtain the reduced row echelon form
We multiply the second row by -1/3 and the third by 1/4
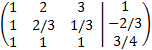
We add the second and the third rows with the first multiplied by -1
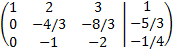
We multiply the second row by -3/4 and the third by -1
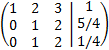
We add the third row with the second one multiplied by -1

This last matrix is in echelon form (but not reduced)
and we don't continue doing operations by row because we can
see that the las row makes the system inconsistent. This row tell us:
$$0x+0y+0z = -1$$
And all this is an impossible equality.
In fact, we have the ranks
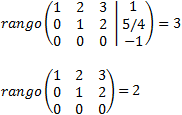
By the Rouché-Capelli Theorem, the system is inconsistent.
System 7
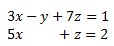
Show Solution
The augmented matrix of the system is
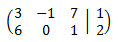
We perform elemental operations in the rows to obtain the reduced row echelon form
We multiply the first and second rows by 1/3 and by 1/6 respectively
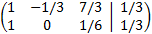
We subtract the second row to the third
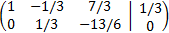
We add the first row with the second
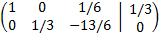
We multiply the third row by 3
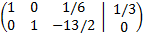
This last matrix is in reduced row echelon form, so we can calculate the ranks easily:
We calculate the ranks
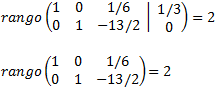
By the Rouché-Capelli theorem, the system is consistent. But it is not Independent because the number of unknown factors (3) is different from the rank.
The matrix we have obtained represents the system
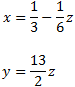
The solutions are
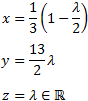
System 8
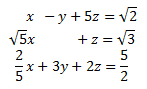
Show Solution
The augmented matrix of the system is
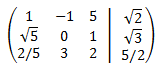
Note: before we start, we should comment that the procedure
will be the same as it has been until now. But we have roots
in the matrix, which means that the operations in the rows will be long
and tedious. This problem isn't very interesting in a didactic sense beyond the calculations.
We perform elemental operations in the rows to obtain
the reduced row echelon form
We add the second row with the first multiplied by -√5 and, with
the third, multiplied by -2/5
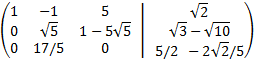
We multiply the second row by 1/√5 and the third by 5/17
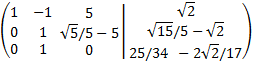
We add the first row with the third and to the second we subtract the third
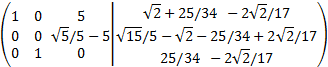
We rewrite the matrix
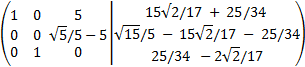
We multiply the second row by (√5/5-5) -1
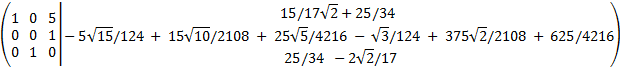
We add the first row with the second one multiplied by -5
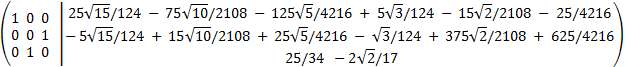
In this last matrix, it's (almost) in row reduced
echelon form (we have to change the second and third rows
so that it's true). From the last matrix we obtain the solutions:
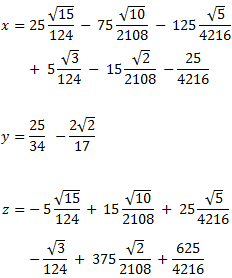
System 9
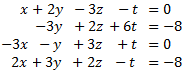
Show Solution
The augmented matrix of the system is
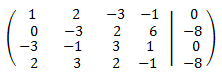
We perform elemental operations in the rows to obtain the reduced row echelon form
We add the third and fourth rows with the first one multiplied by 3 and by -2 respectively
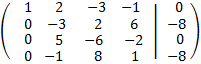
We add the first, the second and the third rows with the fourth multiplied by 2, -3 and 5 respectively
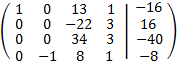
We multiply the fourth row by -1 and we change it with the second
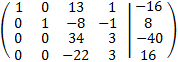
We multiply the third and the fourth rows by 1/34 and -1/22 respectively
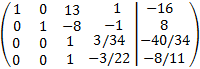
We subtract the third row from the fourth
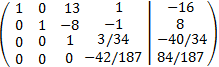
We multiply the fourth by -187/42
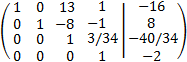
We add to the first row the third multiplied by -13 and and the second by 8
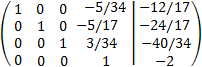
We add to the first row the fourth multiplied by 5/34, to the second we add the first multiplied by
5/17 and to the third we add the first multiplied by -3/34
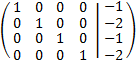
By the Rouché-Capelli theorem, the system is consistent Independent and the solution is
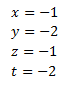
System 10
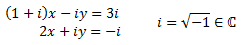
Show Solution
The augmented matrix of the system is
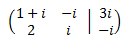
Note: This system was included with the
objective to remark that
the theory of matrix is applicable to the complex numbers.
The only difference with the systems before is that
now we need to operate by multiplying and dividing
complex numbers.
We perform elemental operations in the rows to obtain the reduced row echelon form
We multiply the second row by 1/2 and we change it with the first
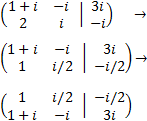
We add a the second row with the first multiplied by –(1+i)
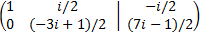
We multiply the second row by
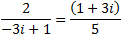
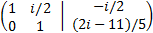
We add the first row to the second multiplied by -i/2
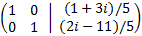
This last matrix is in reduced echelon form because it is the identity matrix.
By the Rouché-Capelli theorem, the system is consistent Independent and the solution is
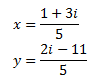

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.