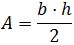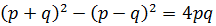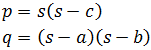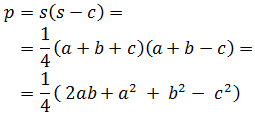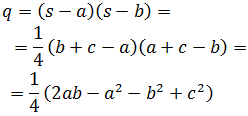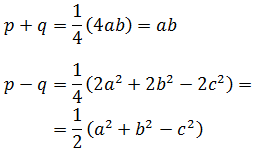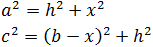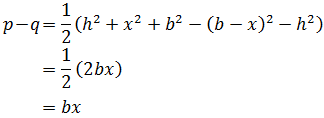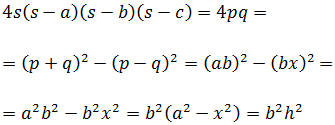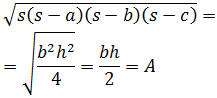Heron of Alexandria

Content of this page:

Heron of Alexandria Biography
Heron's Formula (proved by using the Pythagorean Theorem)
Heron's Method (approximation of the square root of a number):
- 3.1. The Method and some Examples
- 3.2. A Proof of the Convergence

1. Heron of Alexandria Biography

Heron of Alexandria (or Hero of Alexandria) lived in Alexandria (currently the North of Egypt) around the centuries I and II B.C.E. He was a mathematician and engyneer, and invented the first steam engine, which was known as aeolipile (or aeolipyle, or eolipile). In this way, most of the Heron's original writings deal with mathematics and mechanics.

Metrica is a writing divided into three parts where Hero gives formulas and quite rigorous methods to calculate areas of regular polygons, triangles, quadrilaterals and ellipses, as well as the volume of spheres, cylinders and cones.

In this work, Heron states the formula known now as Heron's Formula, which we explain below. We will also use the Heron's Method to approximate square roots of natural numbers. This technique is still used in computer science.

Show References

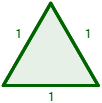
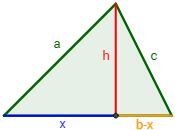
2. Heron's Formula

Heron of Alexandria: biography and Heron's Formula and Heron's Method (area of a triangle and approximation of square roots)

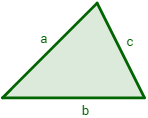
The area of the triangle with sides a, b and c is

$$ Area = \sqrt{s\cdot (s-a) \cdot (s-b) \cdot (s-c)}$$

where s is the semiperimeter of the triangle:

Heron of Alexandria: biography and Heron's Formula and Heron's Method (area of a triangle and approximation of square roots)

Show Example and Proof

Before of proving the Heron’s Formula, let us see an example of an application of the formula:

Example: Calculation of the area of the equilateral triangle of side 1.

Heron of Alexandria: biography and Heron's Formula and Heron's Method (area of a triangle and approximation of square roots)

Since the triangle is equilateral, all of its sides have the same lenght: 1.

Therefore, the semiperimeter is

$$ s = \frac{1+1+1}{2} = \frac{3}{2} $$

By applying the Heron’s Formula, the area of the triangle is:

$$ Area = \sqrt{\frac{1}{2}\cdot \frac{1}{2}\cdot \frac{1}{2}\cdot \frac{3}{2}} = $$

$$ =\frac{1}{2} \cdot \sqrt{\frac{1}{2}\cdot \frac{3}{2}} =$$

$$ =\frac{1}{2} \cdot \sqrt{\frac{3}{4}} =$$

$$ =\frac{1}{4} \cdot \sqrt{3}$$

The following proof of the Heron’s Formula is modern and it only requires the Pythagorean Theorem and a few operations.

We know beforehand that the area of the triangle is

Heron of Alexandria: biography and Heron's Formula and Heron's Method (area of a triangle and approximation of square roots)

where h is the height and b is the base.

To simplify, we will use the following equality:

Heron of Alexandria: biography and Heron's Formula and Heron's Method (area of a triangle and approximation of square roots)

We define p and q as

Heron of Alexandria: biography and Heron's Formula and Heron's Method (area of a triangle and approximation of square roots)

If we write the definition of the semiperimeter s in the previous expressions, we have, on the one hand, that p is

Heron of Alexandria: biography and Heron's Formula and Heron's Method (area of a triangle and approximation of square roots)

and, on the other hand, that q is

Heron of Alexandria: biography and Heron's Formula and Heron's Method (area of a triangle and approximation of square roots)

Then, the addition and the substraction of p and q are respectively:

Heron of Alexandria: biography and Heron's Formula and Heron's Method (area of a triangle and approximation of square roots)

Let us divide the triangle into two right triangles:

Heron of Alexandria: biography and Heron's Formula and Heron's Method (area of a triangle and approximation of square roots)

We have also divided the base b into the segment x and b-x, which are determined by the altitude h.

Since the associated angle to the altitude is right, we can apply the Pythagorean Theorem and we obtain that:

Heron of Alexandria: biography and Heron's Formula and Heron's Method (area of a triangle and approximation of square roots)

We substitute in the expression of p-q:

Heron of Alexandria: biography and Heron's Formula and Heron's Method (area of a triangle and approximation of square roots)

Thus, by using the equality

$$ (p+q)^2 - (p-q)^2 = 4pq $$

and previous operations, we know that

Heron of Alexandria: biography and Heron's Formula and Heron's Method (area of a triangle and approximation of square roots)

(the last equality is by the Pythagorean Theorem).

If we divide by 4 both sides of the equality and do the square root of the resulting sides, then we have that:

Heron of Alexandria: biography and Heron's Formula and Heron's Method (area of a triangle and approximation of square roots)

So, the Heron’s Formula gives the area of the triangle with base b and height h.

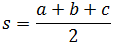
3. Heron's Method

Heron’s Method is about calculating the members of the sequence defined by recursion

Heron of Alexandria: biography and Heron's Formula and Heron's Method (area of a triangle and approximation of square roots)

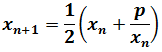
where p is the number whose square root we want to approximate.

The first term, x₀, has to be an approximation to the square root we are looking for.

3.1. The Method and some Examples

Heron’s Method converges fastly: reasonable approximations (with a few of exact decimals) are obtained with a few of iterations, even if the x₀ chosen is very different from the number we want to approximate. Moreover, the implementation of this method is very simple (see the MatLab function).

Let us put the example of the approximation of the square root of 3,

$$ \sqrt{3} \simeq 1.732050807568877 $$

We start with x₀ = 1, x₀ = 2 and x₀ = 100. There will be 10 iterations:

For x₀ = 1:

Heron of Alexandria: biography and Heron's Formula and Heron's Method (area of a triangle and approximation of square roots)

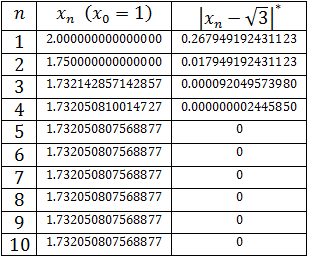
*Note: since the error (third column) is obtained by computing, the error is 0 when the precision of the computer is achieved or surpassed.

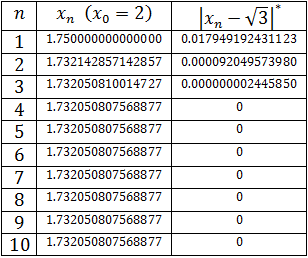
For x₀ = 2:

Heron of Alexandria: biography and Heron's Formula and Heron's Method (area of a triangle and approximation of square roots)

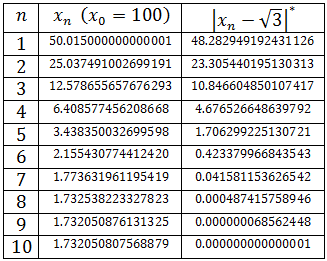
For x₀ = 100:

Heron of Alexandria: biography and Heron's Formula and Heron's Method (area of a triangle and approximation of square roots)

The code we used is:

1   function x=Heron(p,a,n)
2   % approximation of the square root of p
3   % a is the term x_0
4   % n is the number of iterations
5   % x is a column with the format of 
6   % the tables above
7   x=zeros(n,2);
8   x0=a;
9   x(1,1)=0.5*(x0+p/x0);
10  x(1,2)=abs(x(1,1)-sqrt(p));
11  for i = 2:n
12    x(i,1)=0.5*(x(i-1)+p/x(i-1));
13    x(i,2)=abs(x(i,1)-sqrt(p));
14  end
15  end

3.2. Proof of the convergence

We are going to prove that, in fact, the sequence

Heron of Alexandria: biography and Heron's Formula and Heron's Method (area of a triangle and approximation of square roots)

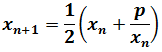
converges to the square root of p.

We will apply the Monotone convergence theorem:

Theorem: Let x_n be a sequence, decreasing and bounded from below. Then, its infimum is the limit:

Heron of Alexandria: biography and Heron's Formula and Heron's Method (area of a triangle and approximation of square roots)

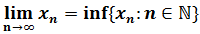
We need to prove that

the sequence is bounded from below, and
it is monotonic decreasing.

a) The sequence is bounded from below by the square root of p:

Heron of Alexandria: biography and Heron's Formula and Heron's Method (area of a triangle and approximation of square roots)

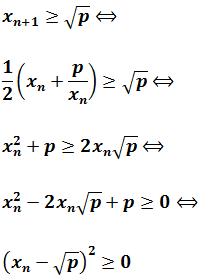
Since the last inequation always holds, the former one so.

b) The sequence is monotonic decreasing:

Heron of Alexandria: biography and Heron's Formula and Heron's Method (area of a triangle and approximation of square roots)

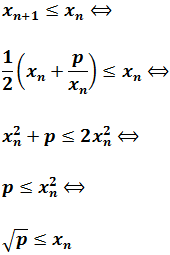
By a), the last inequality is true. Therefore, the former one also holds.

Finally, by applying the Monotone convergence theorem, the sequence converges to the square root of p:

Heron of Alexandria: biography and Heron's Formula and Heron's Method (area of a triangle and approximation of square roots)

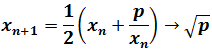
Matesfacil.com by J. Llopis is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.