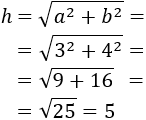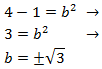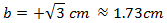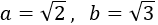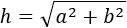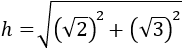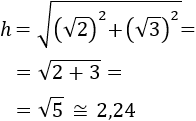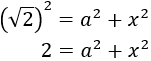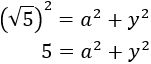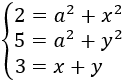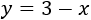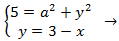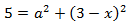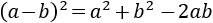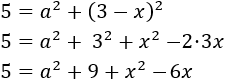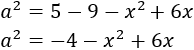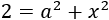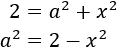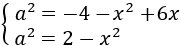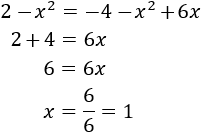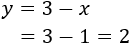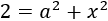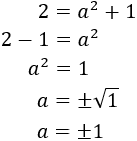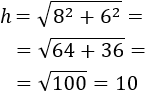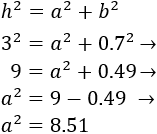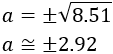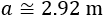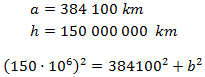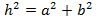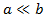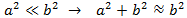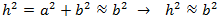Content of this page:
Introduction
Pythagoras' Theorem:
Given a right triangle with sides a and b and a hypotenuse h
(the side opposite the right angle). Then,
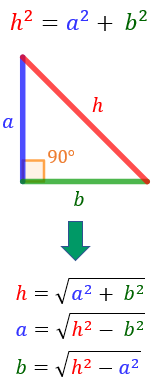
Remember that:
-
A right triangle (right-angled triangle in British English) is a triangle with a right angle (that is, an angle whose measure is \(\frac{\pi}{2}\) rad - 90º).
The hypotenuse is the opposite side as the right angle.
Note: h is always bigger
than the other sides (i.e., h > a and h > b).
The Pythagorean theorem is one of the most known results in mathematics and also one of the oldest known. For instance, the pyramid of Kefrén (XXVI century b. C) was built on the base of the so called sacred Egyptian triangle, a right angled triangle of sides 3,4 and 5. The meaning of the theorem can be easily understood, and there are hundreds of proofs of this theorem. As we will see in the exercises of this section, there are numerous applications of the theorem in real life. In addition, the theorem has uses in advanced mathematics as well (vectorial analysis, functional analysis…).
Solved Problems
Exercise 1
Calculate the hypotenuse of the triangle with sides of 3cm and 4 cm.
Show solution
The sides are
$$a = 3 cm\ ,\ b = 4cm$$
Applying the Pythagoras Theorem,
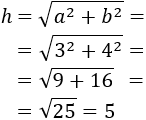
Therefore the hypotenuse measures 5cm.
Exercise 2
If the hypotenuse of a triangle measures 2 cm and one of its sides
measures 1cm, what does the other side measure?
Show solution
Let a and b be the sides of the triangle, and h the hypotenuse.
We know that
$$h=2\ ,\ a=1 $$
By Pythagoras' Theorem,
$$h^2 = a^2 + b^2 $$
Substituting the values we know we have the following equation

Now we isolate b from the equation:
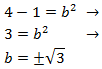
We have written the positive and negative sign because
in theory it's what we must do. But because b
represents a measurement, it can't be a negative number.
Therefore the side measures
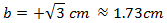
We can leave the square root or reduce it.
Exercise 3
Find the measure of the hypotenuse of a right angled triangle whose sides measure 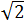 and
and 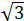 .
.
Show solution
Let a and b be the sides of the triangle,
and h the hypotenuse.
We know that
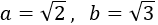
By Pythagoras' Theorem,
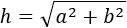
We replace the known values in the equations (a and b),
obtaining:
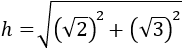
Remember that a square root squared is the radicand
(what is inside the square root sign), so
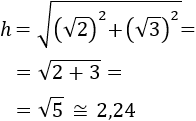
It follows that the hypotenuse measures approximately 2.24.
We do not indicate a unit of measurement because the activity did not provide one.
Exercise 4
Find the height of the following triangle whose sides are
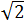 and
and
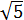 ,
and whose base is 3.
,
and whose base is 3.
Show solution
In order to calculate the height of the triangle, a,
we divide the triangle into two right angle triangles, and then we will apply the Pythagoras’ theorem.
The two triangles are the following ones:
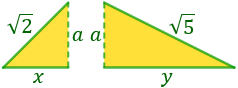
The base of the triangle (value 3) is divided into the two
(the bases of each triangle).
We do not know how much each base measures but we do know that
$$ x+y=3 $$
We apply the Pythagoras theorem to the first triangle and we
obtain the following equation:
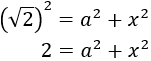
Note that we do not know the sides yet.
Like before, from the other triangle:
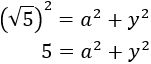
So, we have the following equations:
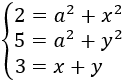
We can isolate y in the third equation, obtaining
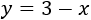
Substituting in the second equation,
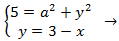
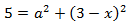
Since we have a squared subtraction, we use the binomial theorem (also called binomial expansion).
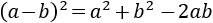
So,
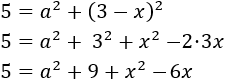
Now we isolate a 2:
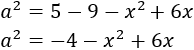
Remember that we also had this equation
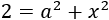
We isolate a 2 from it as well:
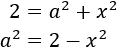
Then, the following equations are obtained
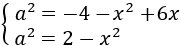
And, as a 2 = a 2, we can
join both expressions obtaining a lineal equation:
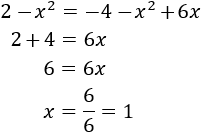
Knowing the value of x we can obtain y:
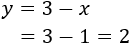
Now we know how much each base measures and we can obtain the height.
The first equation was
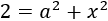
And we know that x = 1, so we have that
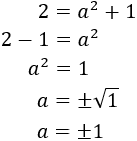
The height a cannot be negative. Hence
$$ a = 1 $$
Exercise 5
Calculate the perimeter of the rhombus if we
know its diagonals (height and width) measure 16 and 12 cm, respectively.
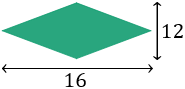
Show solution
We can divide the rhombus in four right angle rectangles
(marked by the diagonal lines):
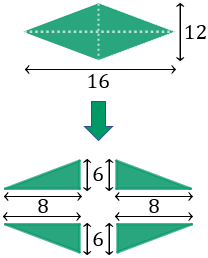
Remember that the rhombus' sides all measure the same,
so we can work with any of the triangles we have
obtained.
As a symmetrical division has been done, it is deduced that the sides measure 8 and 6 in each triangle.
In order to calculate the hypotenuse, we apply the Pythagorean theorem.
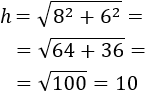
Therefore each side of the rhombus (each hypotenuse) measures 10.
The perimeter is obtained by adding all the sides. Since these
are all the same, we only need to multiply by 4:
Perimeter = 4·10 = 40
Exercise 6
Calculate the height that we can reach with a
3m ladder leaning against a
wall if the bottom of the ladder is 70cm from
the wall.
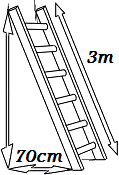
Show solution
We have to take into account that that the units of measurement are not equal.
We can write them all in meters, so
70 cm = 7 dm = 0.7 m
The triangle we have is
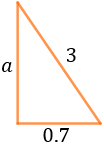
The height is one of the sides. We apply the Pythagorean theorem to calculate it:
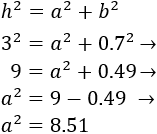
Hence
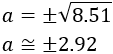
But a has to be positive, because it is a unit of measurement.
So, the height will be, approximately
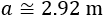
Exercise 7
The distance Sun-Earth-Moon: Let us suppose that The Moon is in the first quarter phase, which means that from Earth we see it the following way:

The white side of The Moon is the side we see (the side illuminated by The Sun).
We know that the distance from Earth to The Moon is 384100Km, and the Earth to The Sun is around 150 million Kilometers. We wish to calculate the distance between The Moon and The Sun in this phase (considering the distances from the centers). Lay out the exercise, but it is not necessary to calculate a result.
Show solution
The situation is the following:
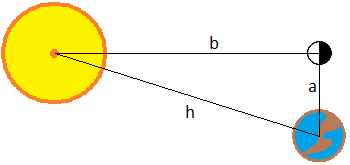
The line Sun-Moon and the line Earth-Moon form a 90 degree angle,
if not, we would not see The Moon in its first quarter. The line Earth-Sun is the hypotenuse.
Therefore we know the distance Earth-Moon (a) and the distance Earth-Sun (h). So,
we can calculate the distance Sun-Moon (b) applying the Pythagoras' Theorem:
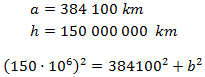
We do not calculate the value of b, because the distance from Earth-Sun is a lot bigger than the distance Earth-Moon and, by approximation, we obtain a similar value to the distance Earth-Sun. But we know the distance Moon-Sun
will be less than the distance Earth-Sun (because this one is the hypotenuse).
Put another way, we know that
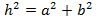
a is much smaller than b, and we express this in the following way:
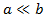
So
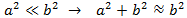
Therefore
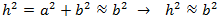

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.

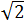 and
and 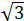 .
.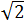 and
and
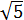 ,
and whose base is 3.
,
and whose base is 3.