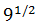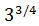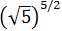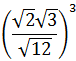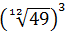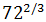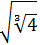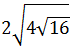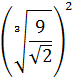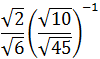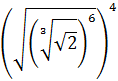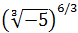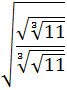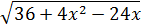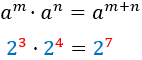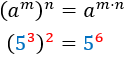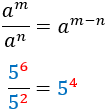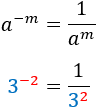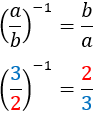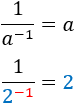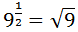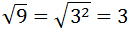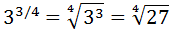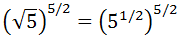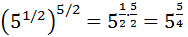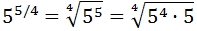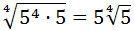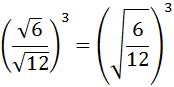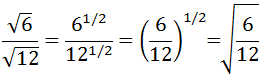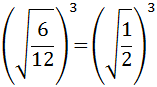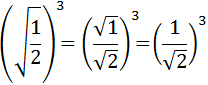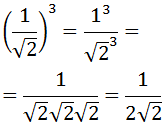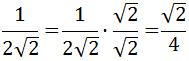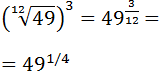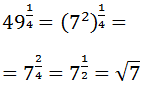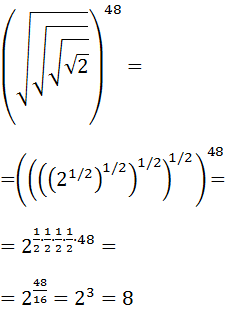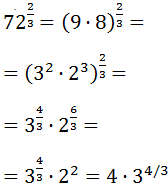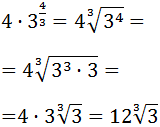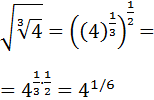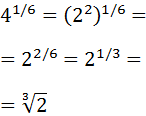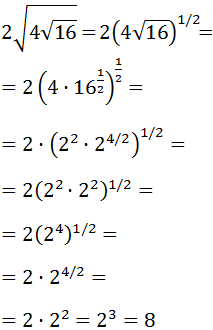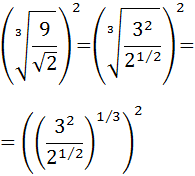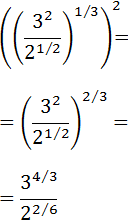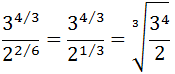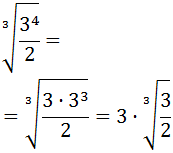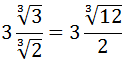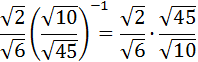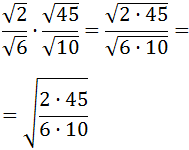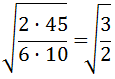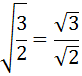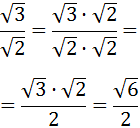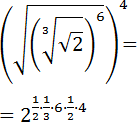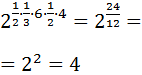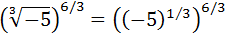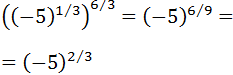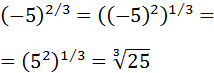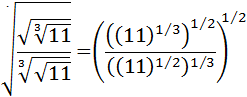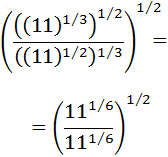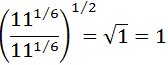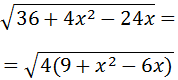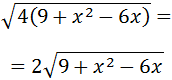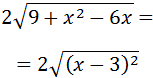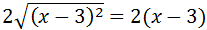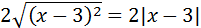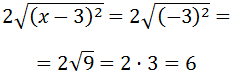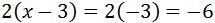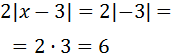Roots as rational or fractional exponents |
|
Content of this page:
-
Introduction
-
Roots as Powers, Properties of Powers, Important Property, Product and Quotient of Roots
-
Solved Exercises: simplifying expressions with roots
Introduction
Power is an expression of this type
ab = a · a · · · a · a
This expression represents the result of multiplying the base, a,
by itself as many times as the exponent, b, indicates.
We read it as "a to the power of b".
In this page we are going to see cases where the exponent, b, is a fraction.
In other words, we are going to work with roots and their powers.
Roots as Powers
Let n be a natural number different from zero (1, 2, 3, 4,...),
We will call the
root of degree n or
nth root of
the number
a to
$$ \sqrt[n]{a} = a^\frac{1}{n} := b,\ b^n = a$$
In other words,
the nth root of the number a is
the number b, that to the power of n is a
(so, b n = a).
The number n is called the degree of the root and a
is called the radicand of the root.
Let's see some special cases:
The root of degree n = 2 is known as
a square root.
Example:
The square root of 9 is 3 because 3 to the power of two is 9.
$$ \sqrt{9} = 3 $$
The root of degree n = 3 is known as
a cube root.
Example:
The cube root of -8 is -2 because -2 to the power of three is -8.
$$ \sqrt[3]{-8} = -2 $$
Important:
There are no roots with an even number degree
(2, 4, 6, 8..) of negative numbers
(they are complex numbers), but there
are roots of negative numbers if the degree is an
uneven number.
PROPERTIES OF POWERS
|
|
Product
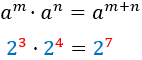
|
Power
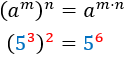
|
| Quotient
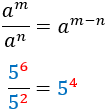
|
Negative exponent
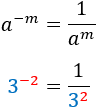
|
| Inverse
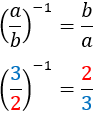
|
Inverse of inverse
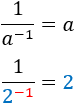
|
Important Property
The following property will probably be the one we will use the most:
$$ a^\frac{b}{c} = \sqrt[c]{a^b} $$
Product and Quotient of Roots
The product of two roots with the same
degree is the root (of same degree) of the product of the radicands,
this is,
$$ \sqrt[n]{a}\cdot \sqrt[n]{b} = \sqrt[n]{a\cdot b} $$
The same happens with the quotient:
$$ \frac{\sqrt[n]{a}}{\sqrt[n]{b}} = \sqrt[n]{\frac{a}{b}} $$
Solved Exercises
Simplify the expressions with fractional exponents
Exercise 1
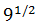
Show solution
We have a square root written in the form of a power. The power represents:
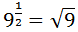
We know that the square root of 9 is 3, but we can write 9 like
9 = 32 to see clearer how the square root disappears
(this is what we will do with more complex expressions):
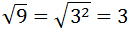
Exercise 2
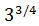
Show solution
We write the power in the form of a root.
Because the denominator of
the exponent is 4, it is a fourth
degree root (fourth root):
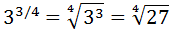
Notice how the numerator, 3, remains as the exponent of the radicand.
We cannot remove any term from the root because
it is a fourth degree root, and to do this the
radicand would need to have an exponent bigger
or equal to 4.
Exercise 3
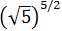
Show solution
We can write the square root in the form of a power to operate with the exponent:
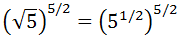
Now we apply the properties of powers:
we have a power of a power, so we multiply the exponents:
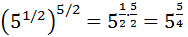
We will write the power in the form of a root (fourth degree):
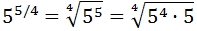
We have expressed the radicand like a product to see
there is a factor we can extract from the
expression. Because it is a fourth root, we can write
a 5 for each 5 4 we have in the radicand:
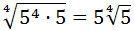
We cannot simplify the expression further.
Exercise 4
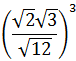
Show solution
Remember that the product of
roots with the same degree is the root
with the same degree of the
product of the radicands:

Because we have a root in the numerator
and denominator (same degree) we can
write them as one single root:
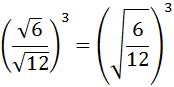
Note: : the step above is due to the properties of powers because
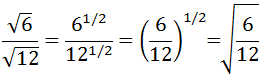
Now we can simplify the radicand's fraction:
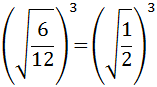
Due to the fact we have a 1 in the
numerator
and its square root is 1, we are going
to write the two roots again:
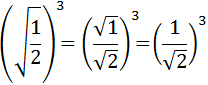
We calculate the cube of the quotient:
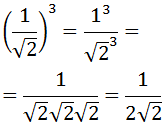
Finally, mathematicians do not like roots in
the denominator, so we multiply in the numerator
and denominator by the root so that it remains
in the numerator:
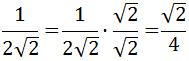
Exercise 5
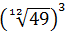
Show solution
We will write the twelfth degree root like a power:
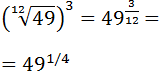
We have simplified the exponent's fraction. Now we will write the radicand (49) as a power:
49 = 7 2.
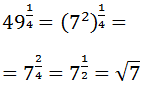
Exercise 6
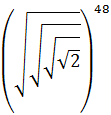
Show solution
This exercise can seem complicated because
there are roots within roots, but the only thing
we need to do is write the square
roots as powers and apply the properties
of powers ( power of a power):
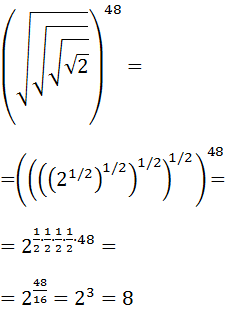
Exercise 7
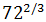
Show solution
We write 72 like a power to apply the properties:
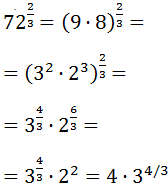
We write the fractional exponent like a cube root and we will be able to extract a factor:
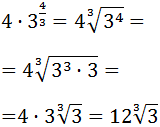
Notice that because it is a cube
root (third degree), we can extract a 3
from the radicand for each 3 3.
Exercise 8
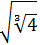
Show solution
We write the roots as powers:
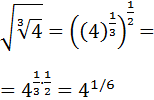
Now we will write 4 as a power, 4 = 2 2, to be able to simplify:
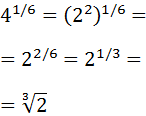
Exercise 9
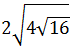
Show solution
We write numbers as well as roots in exponential form to apply the properties:
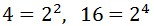
Therefore
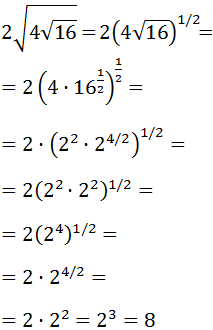
Exercise 10
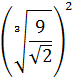
Show solution
We write roots as powers (one is cube and the other is square) and 9 as
9 = 3 2
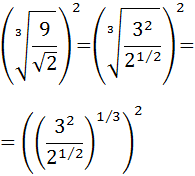
Now we multiply all the exponents (power of a power):
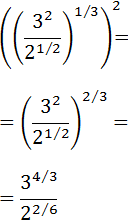
Finally we simplify the fractions in the exponents:
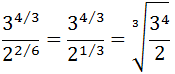
We can extract a factor:
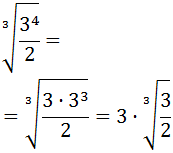
As usual, we will eliminate the root from the denominator.
Because it is a cube root, we have to multiply twice
in the numerator and in the denominator for it to disappear:
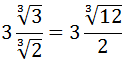
Exercise 11
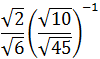
Show solution
Before anything, because we
have a fraction to the power of minus one,
we write the inverse so the exponent disappears:
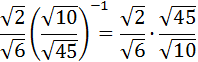
Now, because all the roots are square roots, we can multiply them:
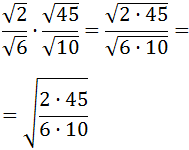
We will simplify the fraction:
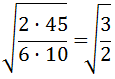
Now we are going to operate a bit to
avoid the root in the denominator: we separate the roots
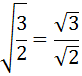
We multiply and divide by the root of 2:
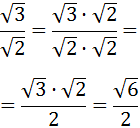
Exercise 12
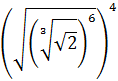
Show solution
The expression is a quite scary, but all we need to do is write all the roots as powers:
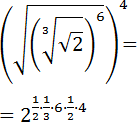
Notice that we have written all the exponents in only one step.
We simplify the exponent:
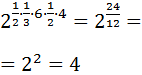
Exercise 13
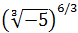
Show solution
We have a root of a negative number, but because it is a cube
root (uneven degree), it exists.
We write the cube root in the form of a power:
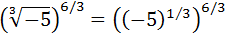
We multiply the exponents (power of a power):
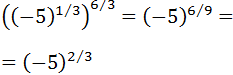
Notice that we can remove the negative sign because (-5) 2 = 5 2
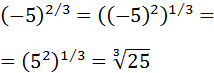
Exercise 14
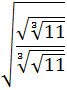
Show solution
We write the five roots as powers:
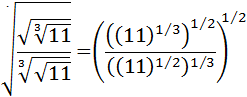
We multiply the exponents (power of a power):
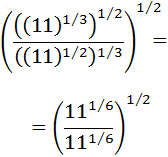
The fraction is 1.
Therefore,
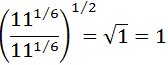
Exercise 15
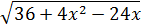
Show solution
We can extract 4 as a common factor in the radicand:
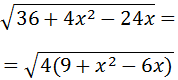
The 4 leaves the square root as 2 (because it is 2 2):
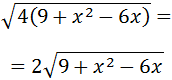
We need to realise that the radicand is a result of Newton's binomial theorem (a subtraction squared):
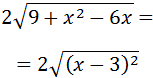
Finally, the root eliminates the square
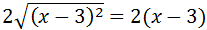
Important: In reality, when we cancel a square root with a
number squared we need to write an absolute value
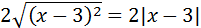
This is due to the fact that if the value of x makes the polynomial
x - 3 negative, (when x < 3 ) then, the power of two makes
the radicand positive and, therefore, the square root exists and is a
positive number. But, if we don't write the number as an
absolute value when we eliminate the root,
we obtain a negative number and, in consequence, a false equality.
Let's see an example:
Let's suppose that x = 0. Then,
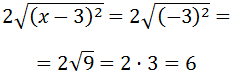
But
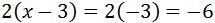
However, if we write the absolute value we get
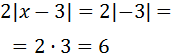

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.