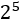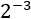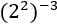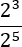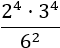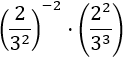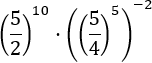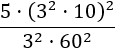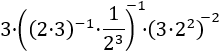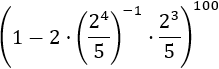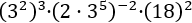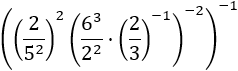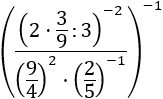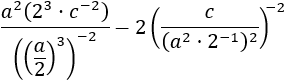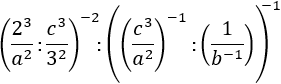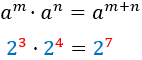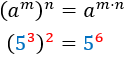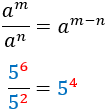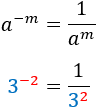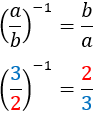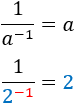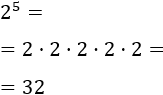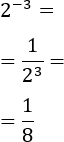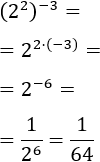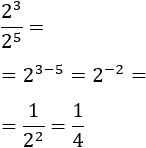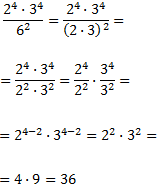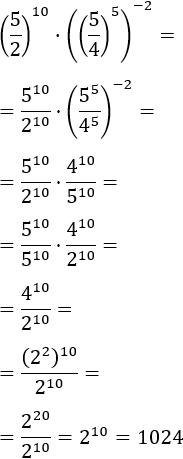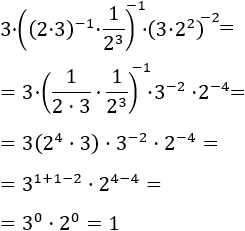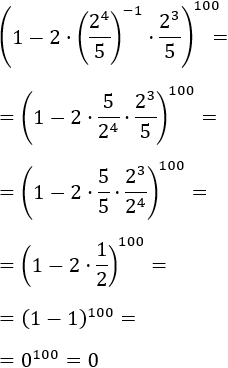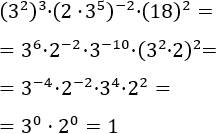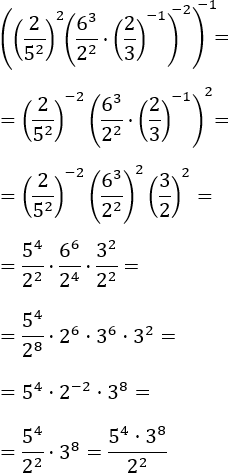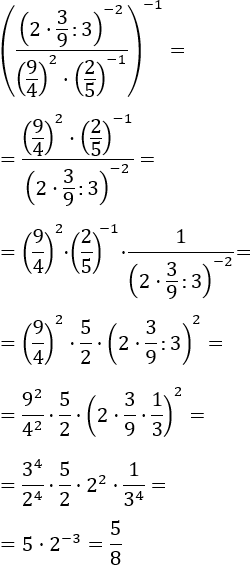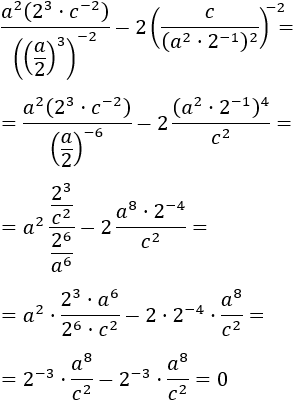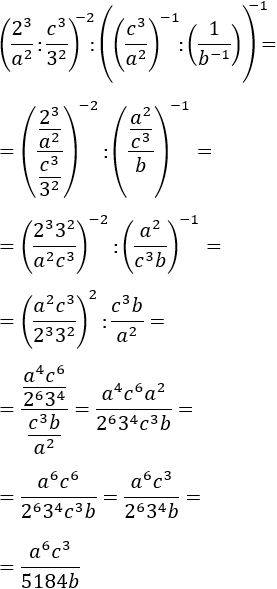Content of this page:
Introduction
Power is an expression of this type
ab = a · a · · · a · a
that represents the result of multiplying the base, a,
by itself as many times as the exponent, b, indicates.
We read it as "a to the power of b".
For example, 2 3 = 2·2·2 = 8
(the base is 2 and the exponent is 3).
Generally, the base as well as the exponent can be any number
(real or complex) or they can even be a variable, unknown factor or parameter.
The equations with the unknown factor is in the exponent are known as exponential equations.
A special case are powers whose exponents are fractions.
In this case, the power represents a square root. They appear due
to the need to solve an equation of the type x n = a.
Another special case are powers with a base of 10, ones with this
appearance 10 n. If n is a natural number (0, 1, 2, 3,...)
the result is 10...0, being n the number of 0's. If n is a negative
number (-1, -2, -3, -4,...), the result is 0.00...1 where the value of n
in positive indicates the number of 0's counting the 0 before the comma. These are the
type of powers used in scientific notation.
Finally, we'll say that the power elevated to 0 is always 1, so, x 0 = 1.
In this section, the activities are in order of increasing difficulty: we use the properties of exponentials (power of products,
power of quotient, power of a power,..) and, after we'll simplify expressions formed by powers
(parenthesis, fractions, negative exponents, parameters..).
PROPERTIES OF POWERS
|
|
Product
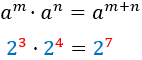
|
Power
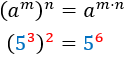
|
| Quotient
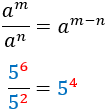
|
Negative exponent
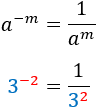
|
| Inverse
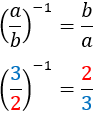
|
Inverse of inverse
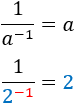
|
Solved Activities
Exercise 1
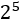
Show solution
We apply the definition of exponentiation, multiplying
the base by itself as many times as the exponent indicates:
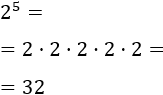
Exercise 2
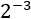
Show solution
If the exponent is negative, first we express the power as a fraction.
The exponent will be the denominator, so we apply the Negative Exponent Rule,
making positive exponents.
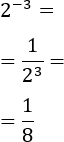
Exercise 3
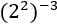
Show solution
When we have a power of a power. We apply the rule that consists in multiplying
both exponents and we obtain a power
with a negative exponent. We continue in the same way as the point
before.
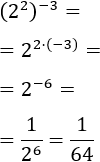
Exercise 4
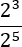
Show solution
We have the quotient of two powers. Because the base is the same,
the rule says that we subtract the exponents
(the numerator's minus the denominator's).
We obtain a negative exponent.
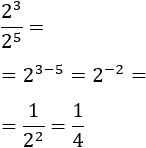
Exercise 5
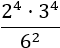
Show solution
We have the multiplication of powers in the numerator, but we can't
resolve it because there are different bases
(2 and 3). In the denominator we have a power with a base
of 6 (3·2).
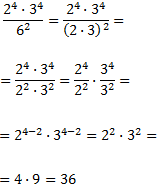
By writing the power in the denominator as the multiplication of powers of
bases 3 and 2, we then have the same
bases in the numerator and denominator and can now
apply the rules.
Exercise 6
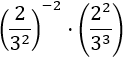
Show solution
First we can eliminate the negative
sign on the exponent of the first power writing the inverse fraction.
That way, we will have a division of powers with the same base.

Exercise 7
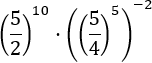
Show solution
We apply the rules of exponentiation to each of them to
simplify the expression.
We transform the bases into others (using powers) to
obtain bases in common.
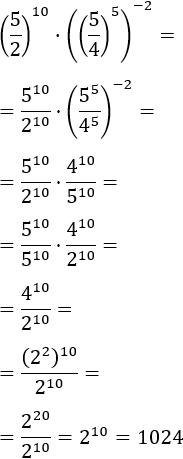
Exercise 8
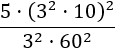
Show solution
The biggest problem in this expression is the amount of different bases that the
powers have. What we will do is break down the bases to prime factors.
Notice that 10 = 2·5 and 60 = 6·10 = 2·3·2·5. After this,
we only have to multiply or divide powers.

Exercise 9
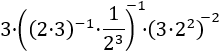
Show solution
We apply the properties of exponentiation,
but first in the parenthesis to begin
eliminating them.
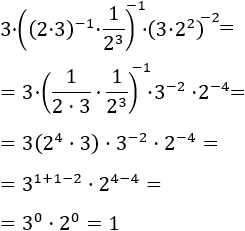
Exercise 10
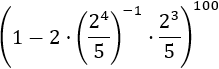
Show solution
We have a high exponent, but we don't need to
worry about it. The important bit of this exercise is that the
base of the power, which is the whole parenthesis, is a subtracting
and we don't have rules to resolve it. Due to this, we have
to do the work inside the parenthesis until we can apply the rules we have.
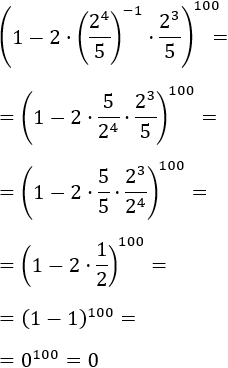
Exercise 11
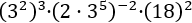
Show solution
We write the base 18 as a product of prime factors and regroup in powers:
18 = 3·6 = 3·2·3.
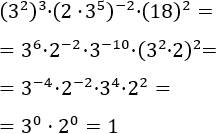
Exercise 12
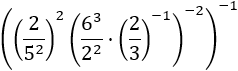
Show solution
We have a lot of exponents. We apply the rule to the first,
which is the power of a multiplication. We have to clearly identify the
factors of the multiplication to apply the rules
without making mistakes. After, we'll continue with
the other exponents.
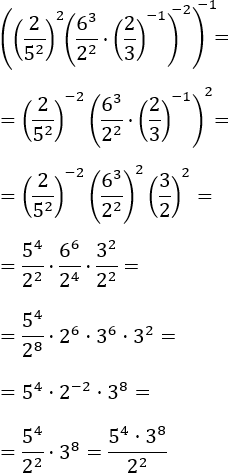
Exercise 13
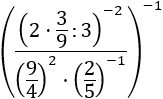
Show solution
We eliminate the first exponent, -1, which means writing the inverse of the base.
We also have different bases, but we already know how to solve this problem:
writing the bases as products of prime factors and regrouping in powers.
We remember that the symbol ":" is a division, the same way as "/" is.
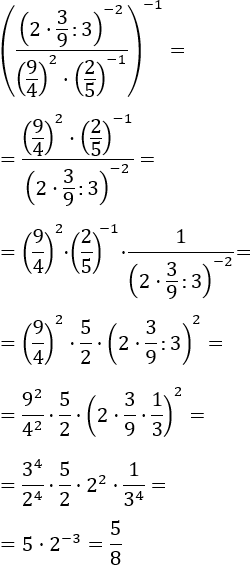
Exercise 14
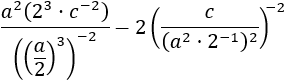
Show solution
The difficulty in this problem is the parameters, or what is the same, the letters.
We work with them the same way as we do with numbers
(the parameters represent numbers after all).
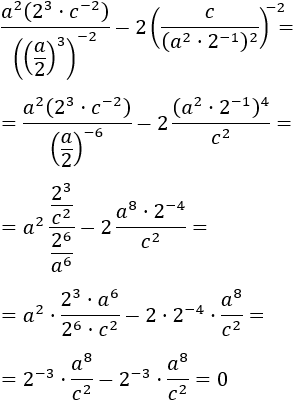
Exercise 15
Show solution
Although it’s simply a issue about writing,
we'll represent divisions ":" in the form of fractions "/".
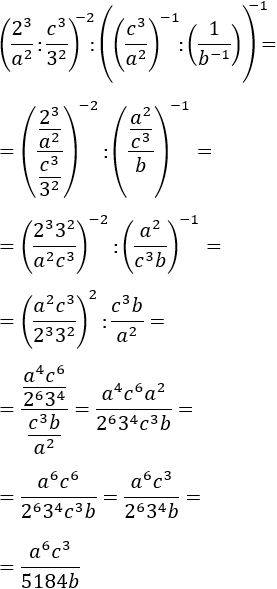

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.