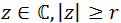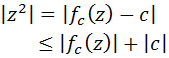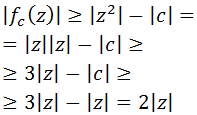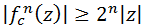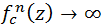Conjunto de Julia Lleno |
Contenido de esta página:
-
Definiciones y Teoremas básicos sobre el Conjunto de Julia (Lleno) de funciones polinómicas de segundo grado
-
Función MatLab para representar un Conjunto de Julia Lleno
Definición 1
Sea f(z) un polinomio con coeficientes complejos, es decir,
$$f(z) = a_n z^n + a_{n-1}z^{n-1}+...+a_1 z + a_0 $$
siendo ai números complejos.
Llamamos Conjunto de Julia Lleno de f al conjunto
$$ K(f) := \{ z \in \mathbb{C} : f^n(z) \nrightarrow \infty \} $$
donde f n es la n-ésima composición de f consigo misma, es decir,
$$ f^1 (z) := f(z) $$
$$ f^2 (z) := f\left(f^1(z) \right) $$
$$ f^3 (z) := f\left(f^2(z) \right) $$
$$ f^n (z) := f\left(f^{n-1}(z) \right) $$
Al término f n (z) de la sucesión anterior lo denominamos n-ésima iterada de f.
Dicho en palabras, el Conjunto de Julia Lleno de la función f está formado por los puntos del plano complejo para los cuales las iteradas de la función en dichos puntos constituyen una sucesión no divergente.
Aunque no pretendemos estudiar en esta página los Conjuntos de Julia, los vamos a definir por las propiedades que podemos demostrar como consecuencia de su definición a partir de los Conjuntos de Julia Llenos.
Definición 2
Bajo las condiciones de la Definición 1, llamamos Conjunto de Julia de la función f al conjunto
$$ J(f) := \partial K(f) $$
Es decir, el Conjunto de Julia de la función f es la frontera del Conjunto de Julia Lleno de f.
Nota: la Definición 2 es, en realidad, una propiedad del caso particular de los Conjuntos de Julia de funciones polinómicas.
Teorema 1
El Conjunto de Julia Lleno de las funciones con la forma
$$ f_c(z) := z^2 + c,\ c\in\mathbb{C}$$
está contenido en el disco de radio
$$ r = max \{ |c|, 3 \} $$
Consecuencia:
El Conjunto de Julia de fc también está en dicho disco (ya que es la frontera del Conjunto de Julia Lleno).
Teorema 2
Para las funciones
$$ f_c(z) = z^2 +c $$
El Conjunto de Julia Completo de fc es compacto.
Consecuencia:
El Conjunto de Julia de fc también es compacto ya que es
$$ J(f_c) = \partial K(f_c) $$
Función MatLab
Para representar el Conjunto de Julia Lleno de
$$ f_c (z) = z^2 +c $$
1 function Julia(n, iter) 2 % n es el número de particiones 3 % x_a (x_b): extremo inf (sup) 4 % para la parte real 5 % y_a (y_b): extremo inf (sup) 6 % para la parte imaginaria 7 % iter: número de iteraciones 8 xa = -2.5; xb = 2.5; 9 ya = -2; yb = 2; 10 v=linspace(xa, xb, n); 11 w=linspace(ya, yb, n); 12 [x,y] = meshgrid(v, w); 13 f = x + 1i * y; 14 m = zeros(size(f)); 15 c=-0.8+0.156*i; 16 k=max(abs(c),3); 17 for p = 1:1:iter 18 f = f.^2 + c; 19 m(abs(f)> k & m == 0) = iter - p; 20 end 21 figure 21 imagesc(m) 22 end
Imágenes del Conjunto de Julia Lleno
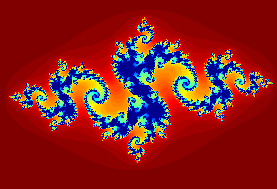
Estas imágenes fueron obtenidas a partir de la función de MatLab del apartado anterior, cambiando los valores de c de la línea 15 de la función.
Las 7 primeras imágenes son el Conjunto de Julia Lleno de la función
$$ f_c(z) = z^2+c $$
y las cuatro últimas son los conjuntos de otro tipo de funciones. Son el resultado de variaciones de la misma función de MatLab.
|
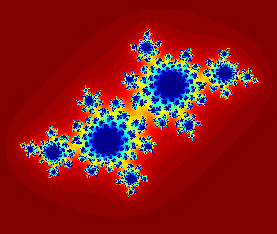
$$ f(z) = z^2 + c $$ $$ c = -0.8 + 0.156i$$
|
|
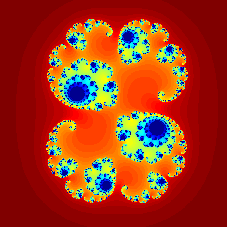
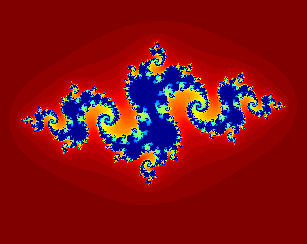
$$ f(z) = z^2 + c $$ $$ c = -0.4+0.6i$$
|
|
$$ f(z) = z^2 + c $$ $$ c = 0.285+0.01i$$
|
|
$$ f(z) = z^2 + c $$ $$ c = -0.835-0.2321i$$
|
|
$$ f(z) = z^2 + c $$ $$ c = 0.8i$$
|
|
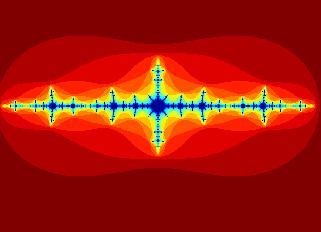
$$ f(z) = z^2 + c $$ $$ c = -1.476 $$
|
|
$$ f(z) = z^2 + c $$ $$ c = -0.79+0.15i $$
|
|
$$ f(z) = \frac{2(z^3-2)}{3z} $$ Triángulo de Sierpinski
|
|
$$ f(z) = \frac{z^2+0.7}{z^2-0.7} $$
|
|
$$ f(z) = z^6 + 1.01z $$
|
|
$$ f(z) = exp(z^3)-0.59 $$
|

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.