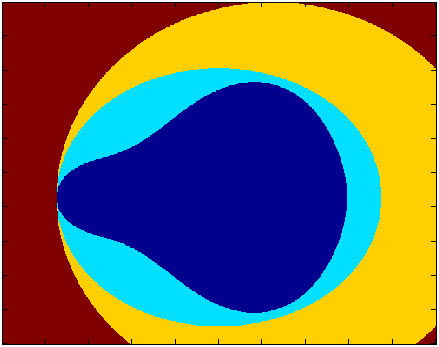
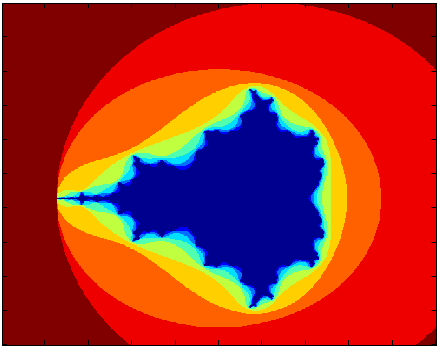
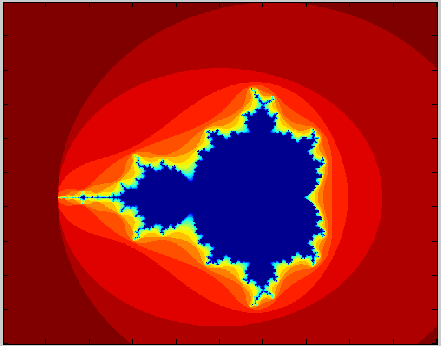
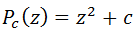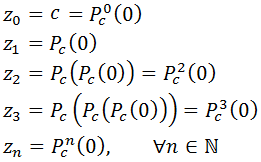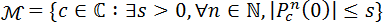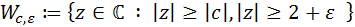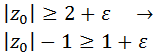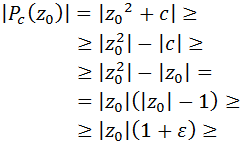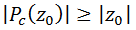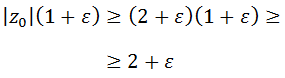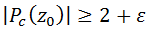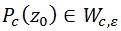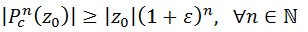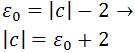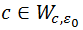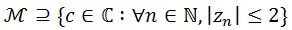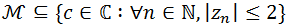Conjunto de Mandelbrot |
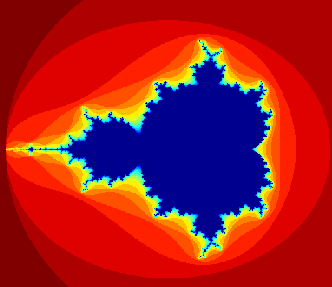
Contenido de esta página:
-
Introducción al Conjunto de Mandelbrot
-
Ejemplos de un punto que está en Mandelbrot y de otro que no lo está
-
Demostración de la definición equivalente a la de Conjunto de Mandelbrot
-
Función de MatLab para representar el fractal y ejemplos
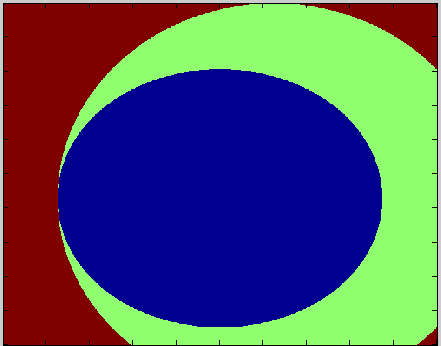
1. Introducción a Mandelbrot (definición)
2. Ejemplos de puntos
3. Demostración de la definición equivalente
4. Función para MatLab
5. Imágenes de Conjuntos Multibrot
Estos conjuntos se obtienen de la generalización del conjunto de Mandelbrot:
En lugar de la sucesión
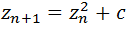
Usaremos la sucesión
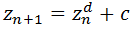
Veamos algunos ejemplos de estos fractales:
|
$$ z_{n+1} = z_n ^{3} + c $$
|
|
$$ z_{n+1} = z_n ^{4} + c $$
|
|
$$ z_{n+1} = z_n ^{5} + c $$
|
|
$$ z_{n+1} = z_n ^{20} + c $$
|
|
$$ z_{n+1} = z_n ^{-2} + c $$
|
|
$$ z_{n+1} = z_n ^{-3} + c $$
|
|
$$ z_{n+1} = z_n ^{-4} + c $$
|
|
$$ z_{n+1} = z_n ^{-5} + c $$
|
|
$$ z_{n+1} = z_n ^{-9} + c $$
|

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.

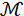 al Conjunto de Mandelbrot, definido por
al Conjunto de Mandelbrot, definido por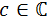 es un punto de
es un punto de 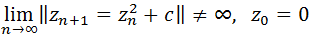

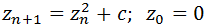
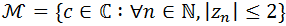
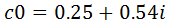
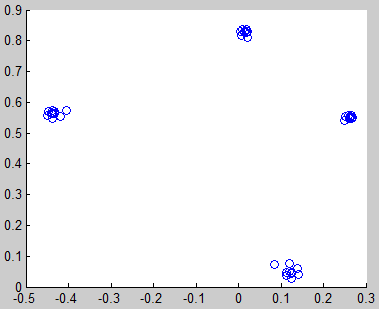
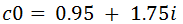
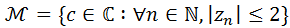
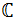 , la función
, la función