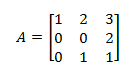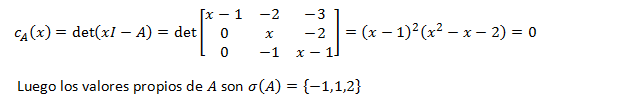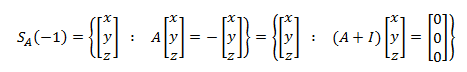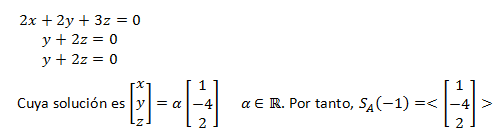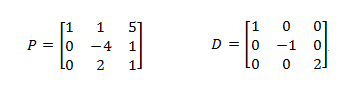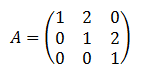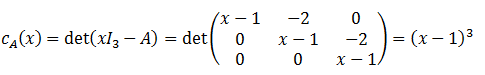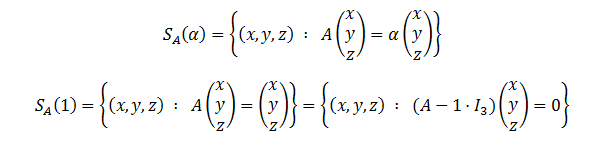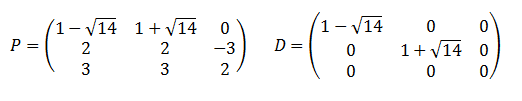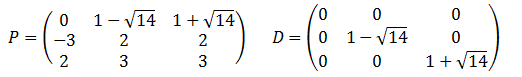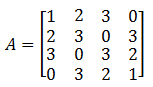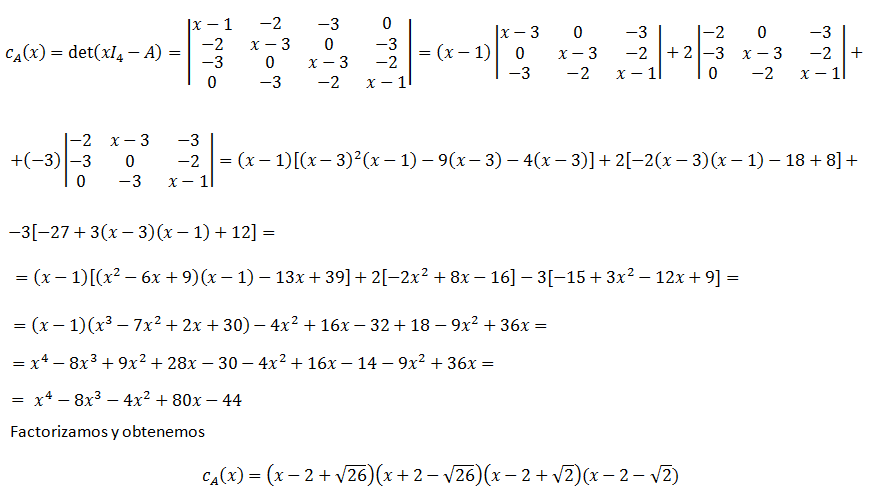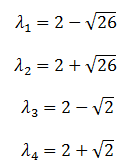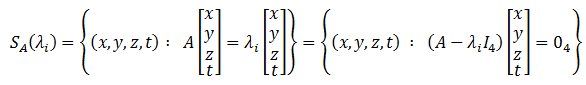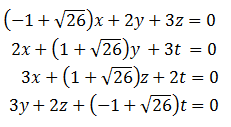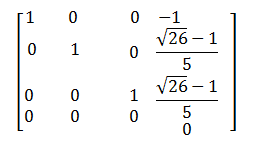Diagonalización de Matrices: Ejercicios Resueltos
Contenido de esta página:
Introducción
Método para diagonalizar una matriz
4 Ejercicios Resueltos
Introducción
En esta sección vamos a diagonalizar, paso a paso, matrices reales cuadradas de dimensiones 3 y 4.
Recordemos que una matriz A cuadrada es diagonalizable si existe una matriz P regular y una matriz D diagonal, ambas de la misma dimensión, de modo que
$$ A = PDP^{-1}$$O equivalentemente,
$$D = P^{-1}AP$$Entre sus propiedades, podemos destacar:
La matriz diagonal D tiene en su diagonal los autovalores (valores propios) de A
La columna i de P es el vector propio asociado al autovalor de la posición i de la diagonal de D
Teorema: todas las matrices reales y simétricas son diagonalizables.
-
Potencias de A:
$$A^2 = AA = (PDP^{-1})(PDP^{-1}) =P D^2 P^{-1}$$Por inducción,
$$A^k =P D^k P^{-1}$$Y como D es diagonal, notemos que
$$D^k = diag(d^k_1,d^k_2 ,...,d^k_n)$$Así que calcular las potencias de A es muy rápido.
Podemos encontrar aquí más teoría de diagonalización de matrices.
Método para diagonalizar una matriz
Consideremos la matriz A de dimensión n
Obtener los valores propios de la matriz A
Buscar una base de los subespacios asociados a los valores propios
Si la unión de las bases es una base de
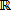 n
(la suma de las dimensiones de los subespacios es n) la matriz es
diagonalizable.
n
(la suma de las dimensiones de los subespacios es n) la matriz es
diagonalizable.Construir P cuyas columnas sean la base obtenida (por tanto, es regular) y construir
$$D = diag(d_1,d_2 ,...,d_n)$$donde di es el valor propio asociado al vector propio de la columna i de P.
Entonces tendremos
$$A = PDP^{-1}$$
Ejercicios Resueltos
Ejemplos (click para ver solución) |
|||
|---|---|---|---|
| 1 |
| ||
| 2 |
| ||
| 3 |
| ||
| 4 |
| ||

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.