Diagonalización de Matrices (Teoría)

Introducción

En esta sección presentamos el concepto de matriz diagonalizable para un cuerpo en general. Enumeraremos las propiedades (directas de la demostración) y otros teoremas. Además, exponemos un método para diagonalizar matrices.

También podemos encontrar aquí ejemplos para factorizar (diagonalizar) matrices paso a paso.

Las definiciones y resultados los damos para un cuerpo en general y así tener una teoría más amplia, pero podemos considerar, por ejemplo que K = .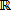

Los conceptos claves que necesitamos son: matrices, autovalores, autovectores, polinomio característico de matrices, matrices simétricas, subespacios vectoriales y las propiedades de las matrices.

Definición de matriz diagonalizable

Sea A una matriz de K ^{n x n}, donde K es un cuerpo (como lo son los reales o los complejos) decimos que es diagonalizable en K si existen dos matrices cuadradas, P y D, de la misma dimensión que A y sobre K tales que

• P es regular,

• D es diagonal y

• A = PDP^-1

  (o, equivalentemente, P^-1AP = D).

Veamos dos ejemplos:

1. La siguiente matriz real A es diagonalizable en los reales y, por tanto, en los complejos

   

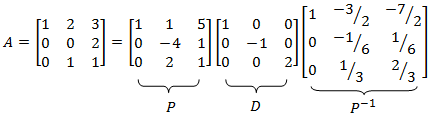
2. La matriz real B es diagonalizable en los complejos pero en los reales (puesto que sus valores propios son complejos).

   

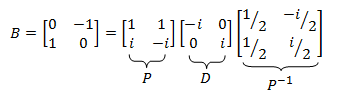
Propiedades inmediatas de la definición

Las siguientes propiedades se demuestran directamente a partir de la propia definición de matriz diagonalizable

• A es semejante a D

• Si A es real y diagonalizable en los reales, lo es en los complejos (los reales son subespacio de los complejos).

• La matriz P no es única (existen infinitas posibilidades para la factorización):

  Podemos, por ejemplo, multiplicar P por un escalar no nulo y P^-1 por su inverso.

• Si A = PDP ^-1 es una diagonalización de A, la matriz diagonal

  $$D = diag(d_1,d_2,…,d_n)$$

  está formada por autovalores de A y el vector de la columna i de la matriz P es un vector propio asociado al autovalor d_i .

Método para diagonalizar

Si A es diagonalizable en los reales, para obtener las matrices P y D procedemos del siguiente modo:

1. Obtener los valores propios de la matriz A

2. Buscar una base de los subespacios asociados a los valores propios (la unión de todas ellas es una base de ⁿ).

3. construir P cuyas columnas sean la base obtenida y construir

   $$D = diag(d_1, d_2,..., d_n)$$

   donde d_i es el valor propio asociado al vector propio de la columna i de P.

Ver ejemplos.

Otras propiedades y teoremas:

• Teorema 1: Sea A una matriz de K ^{n x n}, es diagonalizable si, y sólo si, la suma de las dimensiones de los subespacios asociados a los autovalores de A es n. Y esto es equivalente a que exista una base de K ⁿ formada por vectores propios de A.

• Teorema 2: Una matriz A real de dimensión n (cuadrada) es diagonalizable en los reales (y, por tanto, en los complejos) si y sólo si existe una base de ⁿ formada por vectores propios de A.

  Ver demostración.

• Consecuencias Teorema 2:

  • Si el espectro de A (el conjunto de valores propios de A ) no son reales, la matriz no es diagonalizable en los reales.

  • Se prueba fácilmente por inducción que

    $$A^k = PD^k P^{-1}$$

    siendo k un natural. Propiedad interesante para el cálculo de potencias ya que de esta forma sólo tenemos que calcular el producto de tres matrices porque como D diagonal, sus potencias son

    $$D^k = diag(d^k _1, d^k_2,..., d^k_n)$$



• Teorema 3: Toda matriz real y simétrica A es diagonalizable. Además, se tiene que A = PDP^-1 donde D es diagonal y P ortogonal (P ^-1 = P ^T).

  Ver demostración.