Contenido de esta página:
Introducción: concepto de la unión y la intersección de intervalos y ejemplos.
Test en línea de 15 preguntas
Recordamos que un intervalo \(\left[a,b\right]\) de \(\mathbb{R}\) es el conjunto de los números \(x\in\mathbb{R}\) tales que \(a\leq x\leq b\). Además, los extremos pueden ser abiertos o cerrados. Más información: Intervalos I.
Si \(A\) y \(B\) son dos intervalos, entonces se define la unión \(A\cup B\) como el conjunto de puntos \(x\) que están en el intervalo \(A\) ó en el intervalo \(B\) (o en ambos intervalos):
$$ A \cup B = \{x \ | \ x \in A \lor x\in B \} $$
Ejemplos:
La unión \(\left[0,1\right] \cup \left[1,2\right]\) es el intervalo \(\left[0,2\right]\):
La unión \(\left(0,1\right] \cup \left[1,2\right)\) es el intervalo \(\left(0,2\right)\):
La unión \(\left[0,1\right) \cup \left(1,2\right]\) no puede escribirse como un único intervalo ya que se excluye el punto 1:
$$\left[0,1\right) \cup \left(1,2\right] = \left[0,2\right]-\{1\}$$
Si \(A\) y \(B\) son dos intervalos, entonces se define la intersección \(A\cap B\) como el conjunto de puntos \(x\) que están en el intervalo \(A\) y en el intervalo \(B\). Es decir, es el conjunto de puntos que están en ambos intervalos:
$$ A \cap B = \{x \ |\ x \in A \land x\in B \} $$
Ejemplos:
La intersección \(\left[0,2\right] \cap \left[1,3\right]\) es el intervalo \(\left[1,2\right]\):
La intersección \(\left(0,2\right] \cap \left(1,3\right)\) es el intervalo \(\left(1,2\right]\):
La intersección \(\left[0,1\right) \cap \left[1,2\right]\) es vacía ya que no hay ningún punto común en ambos intervalos:
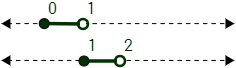
$$\left[0,1\right) \cap \left[1,2\right) = \emptyset $$
Escoger la opción equivalente a la unión
$$\left[0,2\right] \cup \left[2,4\right] $$
|
$$ \left[0, 2\right] $$
|
|
|
$$ \left[0, 4\right] $$
|
|
|
$$ \left[2, 4\right] $$
|
Escoger la opción equivalente a la unión
$$\left[-1,2\right) \cup \left[2,3\right) $$
|
$$ \left[-1, 3\right] $$
|
|
|
$$ \left(-1, 3\right] $$
|
|
|
$$ \left[-1, 3\right) $$
|
Escoger la opción equivalente a la unión
$$\left(-\infty,-2\right) \cup \left[-2,0\right) $$
|
$$ \left(-\infty, 0\right] $$
|
|
|
$$ \left(-\infty, 0\right) $$
|
|
|
$$ \left[-\infty, 0\right) $$
|
Escoger la opción equivalente a la unión
$$\left(-1,1\right) \cup \left(0,1\right] $$
|
$$ \left(-1, 1\right] $$
|
|
|
$$ \left(-1, 1\right) $$
|
|
|
$$ \left[-1, 1\right) $$
|
Escoger la opción equivalente a la unión
$$\left(-\infty,0\right) \cup \left(0,+\infty \right) $$
|
$$ \left(-\infty, +\infty \right) $$
|
|
|
$$ \mathbb{R} $$
|
|
|
$$ \mathbb{R}-\{0\} $$
|
Escoger la opción equivalente a la unión
$$\left(0,2\right) \cup \left(2,3\right) $$
|
$$ \emptyset $$
|
|
|
$$ \{2\} $$
|
|
|
$$ \left(0,3\right)-\{2\} $$
|
Escoger la opción equivalente a la unión
$$\left[-3,2\right] \cup \left(1,4\right) \cup \left(4,5\right) $$
|
$$ \left[-3, 5\right)-\{1\} $$
|
|
|
$$ \left(-3, 5\right)-\{4\}$$
|
|
|
$$ \left[-3, 5\right) -\{4\} $$
|
Escoger la opción equivalente a la intersección
$$\left[0,2\right] \cap \left[1,3\right] $$
|
$$ \left[1, 2\right] $$
|
|
|
$$ \left(1, 2\right) $$
|
|
|
$$ \left[1, 3\right]$$
|
Escoger la opción equivalente a la intersección
$$\left[-1,2\right] \cap \left(1,2\right) $$
|
$$ \left[1, 2\right) $$
|
|
|
$$ \left(1, 2\right) $$
|
|
|
$$ \left[-1, 2\right) -\{1\} $$
|
Escoger la opción equivalente a la intersección
$$\left[-5,-3\right] \cap \left(-3,4\right) $$
|
$$ \left[-3,4\right) $$
|
|
|
$$ \left(-3, 4\right) $$
|
|
|
$$ \emptyset $$
|
Escoger la opción equivalente a la intersección
$$\left[-1,3\right) \cap \left(2,4\right] $$
|
$$ \left(2, 3\right) $$
|
|
|
$$ \left(2, 4\right] $$
|
|
|
$$ \emptyset $$
|
Escoger la opción equivalente a la intersección
$$\left(-\infty,0\right] \cap \left[0,+\infty\right) $$
|
$$ \mathbb{R}-\{0\} $$
|
|
|
$$ \emptyset $$
|
|
|
$$ \{0\} $$
|
Escoger la opción equivalente a la intersección
$$\left(-\infty,1\right) \cap \left(-1,+\infty\right) $$
|
$$ \left(-1, 1\right) $$
|
|
|
$$ \left[-1, 1\right] $$
|
|
|
$$ \emptyset $$
|
Escoger la opción equivalente a la intersección
$$ \left[-10,10\right) \cap \left(1,8\right)\cap \left[1,5\right) $$
|
$$ \left[1, 5\right) $$
|
|
|
$$ \left(1, 5\right) $$
|
|
|
$$ \left[1, 5\right] $$
|
Escoger la opción equivalente a la intersección
$$\left[1,2\right] \cap \left(2,3\right] \cap \left[3,4\right) $$
|
$$ \left(2, 3\right) $$
|
|
|
$$ \left(2, 3\right] $$
|
|
|
$$ \emptyset $$
|
Intervalos II: unión e intersección - (c) - matesfacil.com
Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.
