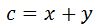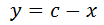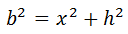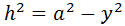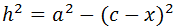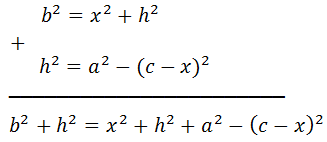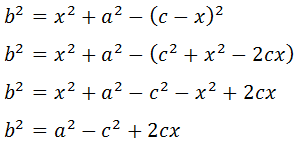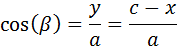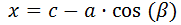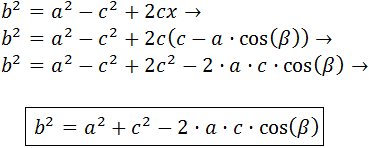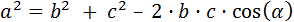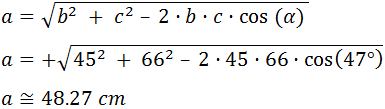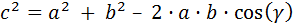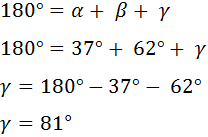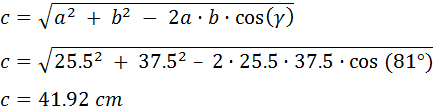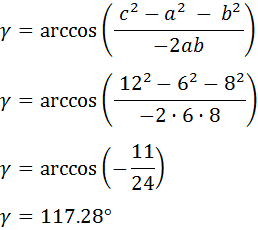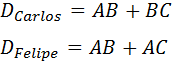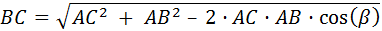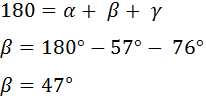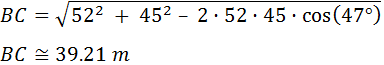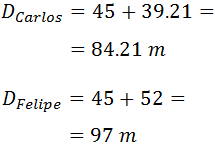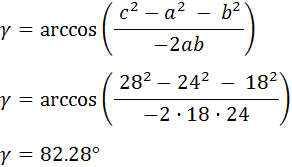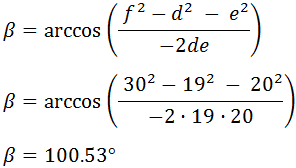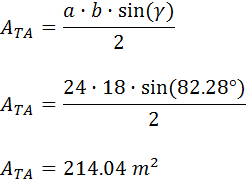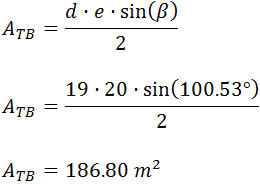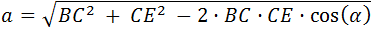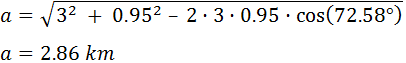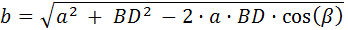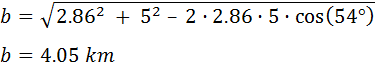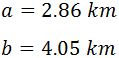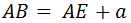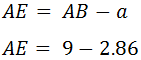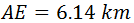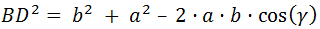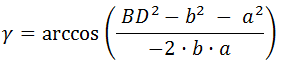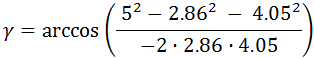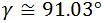Teorema del coseno o de los cosenos
Contenido de esta página:
-
Introducción
-
Teorema del coseno (enunciado y demostración)
-
6 Problemas resueltos de aplicación del teorema del coseno
1. Introducción
El teorema del coseno (o teorema de los cosenos) es un resultado de trigonometría que establece la relación de proporcionalidad existente entre las longitudes de lados de un triángulo cualquiera con los cosenos de sus ángulos interiores opuestos. Este teorema es una generalización del teorema de Pitágoras (la razón de ello se encuentra en la nota del siguiente apartado).
Para aplicar el teorema del coseno se necesita conocer la longitud de dos lados y la medida de un ángulo interior (opuesto al del otro lado).
En esta página enunciamos y demostramos el teorema del coseno y resolvemos problemas de su aplicación en los que se pregunta por algún lado o ángulo de un triángulo dado. En algunos de los problemas se necesitan otros resultados básicos como el teorema de Pitágoras y la propiedad de que la suma de los ángulos internos de un triángulo es 180º.
2. Teorema del coseno
Sea un triángulo cualquiera con lados \(a\), \(b\) y \(c\) y con ángulos interiores \(\alpha \), \(\beta \) y \( \gamma \) (son los ángulos opuestos a los lados, respectivamente).
Entonces, se cumplen las relaciones
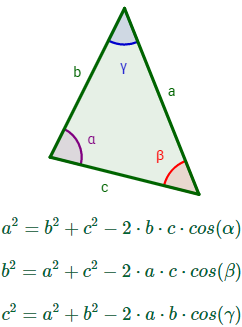
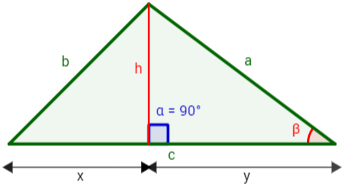
Nota: se dice que es una generalización de Pitágoras porque si uno de los ángulos es recto, el triángulo es rectángulo, siendo la hipotenusa el lado opuesto a dicho ángulo y se obtiene el teorema de Pitágoras al aplicar el del coseno.
Por ejemplo, si α = 90º, entonces, la primera de las tres fórmulas anteriores queda como
$$a^2 = b^2 + c^2$$
siendo a la hipotenusa del triángulo.
6 Problemas Resueltos
Notas previas:
-
En el texto, escribiremos coseno de \( x\) como \(cos(x)\).
-
También utilizaremos la función arcocoseno escrita como \(arccos\), que es la función inversa del coseno. Normalmente, en las calculadoras esta función se denota por \(cos^{-1}\).
Problema 1
Se tiene un triángulo cuyos lados b y c miden 45 y 66 cm respectivamente y cuyo ángulo α mide 47°. Hallar cuánto mide el lado a del triángulo.
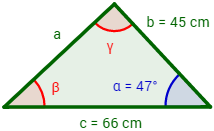
Problema 2
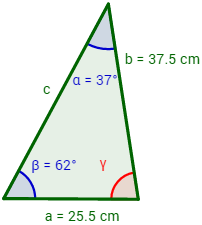
Si cierto triángulo tiene un lado de 25.5 cm y otro de 37.5 cm y sus respectivos ángulos opuestos son de 37° y 62°, ¿cuánto mide el otro lado?
Problema 3
¿Cuál es el valor del ángulo γ del siguiente triángulo si se sabe que los lados a, b y c miden 6, 8 y 12 cm respectivamente?
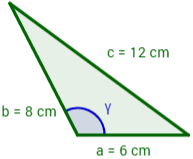
Problema 4
Carlos y Felipe deciden competir en carreras alrededor de un parque. El parque tiene forma de triángulo con vértices A, B y C, ángulos α = 57° y γ = 76º y lados AC = 52 m y AB = 45 m.
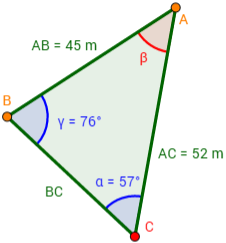
Carlos parte del vértice A y Felipe parte del vértice B. La meta para ambos es el vértice C, pero cada uno debe pasar por el vértice del cual partió el otro antes de dirigirse hacia C. Si los dos corren a la misma velocidad y salen al mismo tiempo, ¿cuál de los dos amigos ganará la competición?
Problema 5
Un labrador quiere comprar un terreno con forma triangular. Se le ofrecen dos terrenos colindantes: el terreno A y el terreno B. La longitud de las tres vallas que delimitan el terreno A son 18, 24 y 28 metros y las del terreno B son 19, 20 y 30 metros.
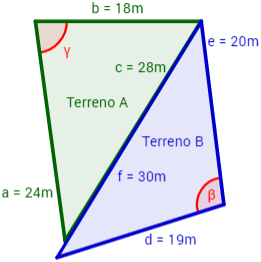
¿Qué terreno debe comprar el labrador si desea el de mayor área?
Ayuda: el teorema del seno establece que el área de un triángulo de lados a, b, c y ángulo γ opuesto al lado c es
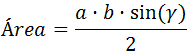
Problema 6
El trayecto de un cuadriatlón (competición deportiva de cuatro disciplinas) está trazado entre cinco puntos (o vértices): A, B, C, D y E.
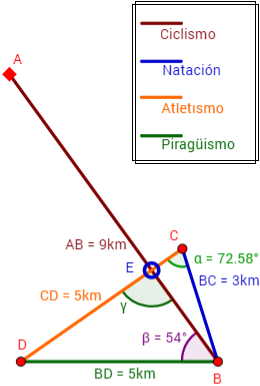
El tramo AB son 9km de ciclismo, el tramo BC son 3km de natación, el tramo CD son 5km de atletismo y el tramo BD son 5km de piragüismo.
En el vértice E hay una parada para tomar agua, la distancia entre los vértices C y E es de 0.95km y los ángulos α y β miden 72.58° y 54° respectivamente.
Calcular:
Distancias a (tramo EB) y b (tramo DE).
Distancia del inicio a la parada a tomar agua (tramo AE).
Ángulo γ.
Teorema del coseno o de los cosenos - (c) - matesfacil.com

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.