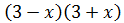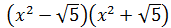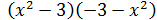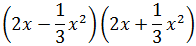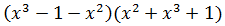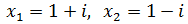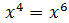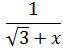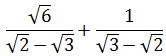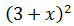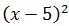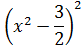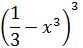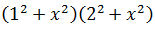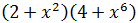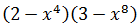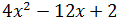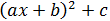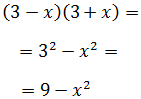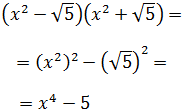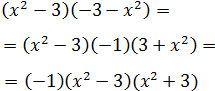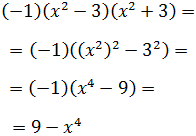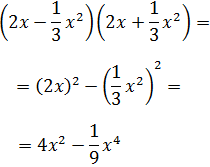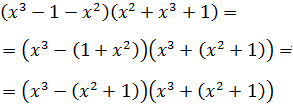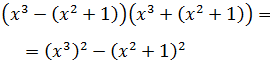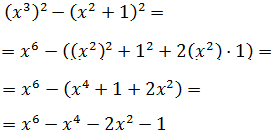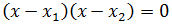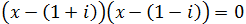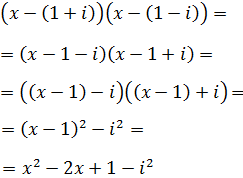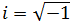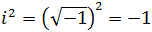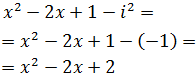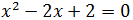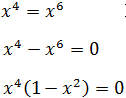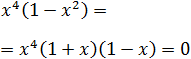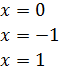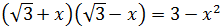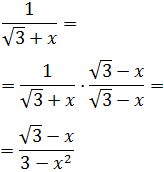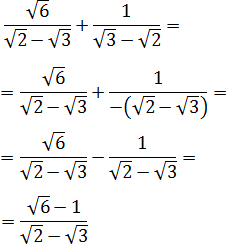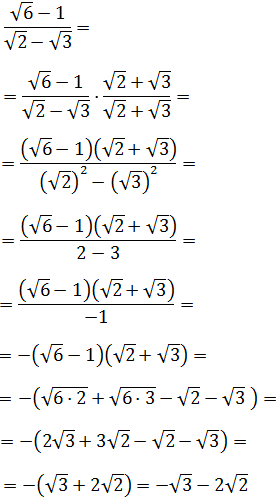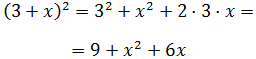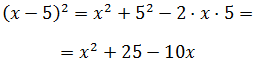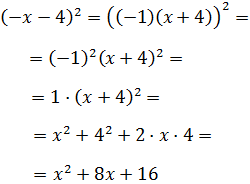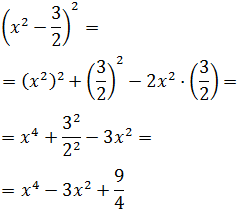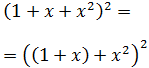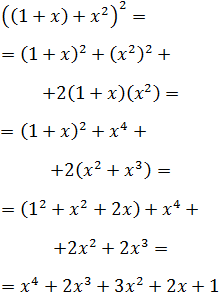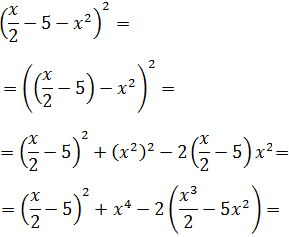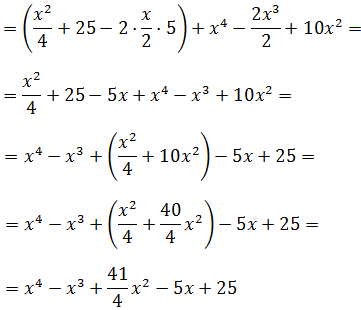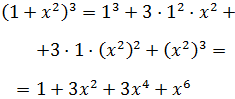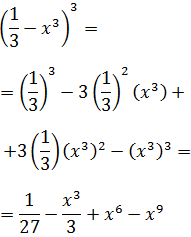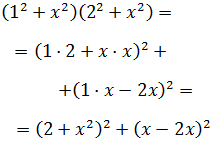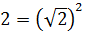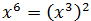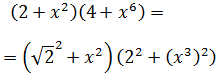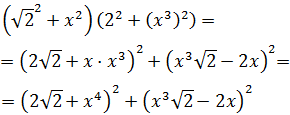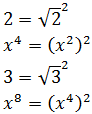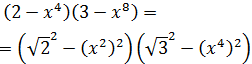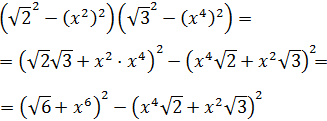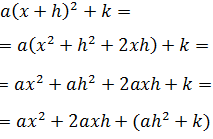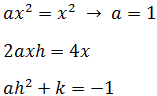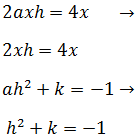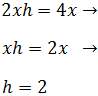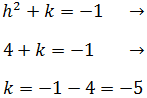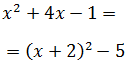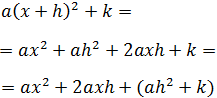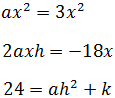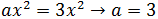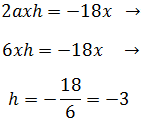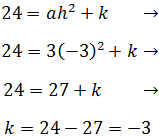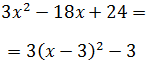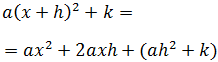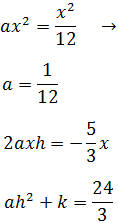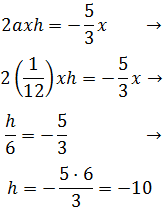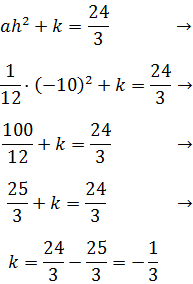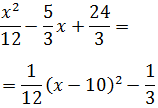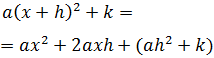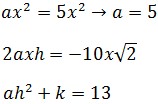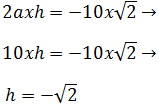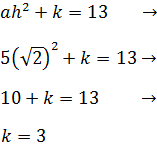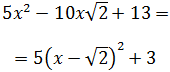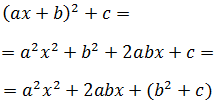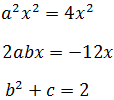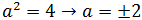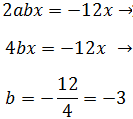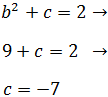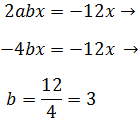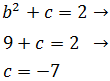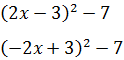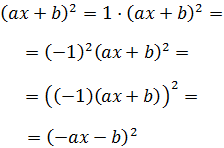Producto Notables:
Fórmulas, Demostraciones y Ejercicios
Contenido de esta página:
Introducción
Suma por diferencia
Binomios al cuadrado y al cubo
Identidades de Lagrange
Completación de cuadrados
-
25 Ejercicios resueltos
0. Introducción
Algunas operaciones (productos sobre todo) aparecen habitualmente en la literatura matemática. Para simplificar los cálculos, se escriben directamente los resultados de estas operaciones aplicando una sencilla fórmula fácil de recordar. Estas fórmulas se conocen como productos notables.
Los productos notables más comunes son la suma por diferencia y el cuadrado de un binomio. En esta página vamos a ver estos y otros productos notables, a demostrar sus respectivas fórmulas y a emplearlas en los ejercicios.
1. Suma por diferencia
$$(a + b)(a - b) = a^2-b^2$$
Esta fórmula se lee como suma por diferencia es igual a la diferencia
de los cuadrados.
Ejemplo:
$$ (x+2)(x-2)=x^2-4 $$
Hemos identificado a = x y b = 2.
Ver demostración
Lo único que tenemos que hacer es desarrollar analíticamente los
productos (propiedad distributiva del producto):
$$ (a+b)(a-b)= $$
$$ =a \cdot a+a\cdot (-b)+ $$
$$ +b \cdot a+ b\cdot (-b)= $$
$$ =a^2 - a\cdot b+ b\cdot a -b^2= $$
$$ =a^2-b^2 $$
Nota: hemos utilizado la propiedad
conmutativa (de los números reales):
$$ a\cdot b = b\cdot a \rightarrow $$
$$ b\cdot a- a\cdot b=0 $$
2. Binomios al cuadrado y al cubo
Un binomio es una suma o una resta de dos elementos, por ejemplo:
Una potencia de binomios es
(a + b)···(a + b) = (a + b) n
Nosotros veremos los casos n = 2 (cuadrado) y n = 3 (cubo).
Las fórmulas para el cuadrado y el cubo son:
Cuadrado de la suma
$$(a + b)^2 = a^2+ 2ab + b^2$$
Ejemplo:
$$ (x+1)^2 = x^2 +2x +1 $$
Ver demostración
La demostración consiste en desarrollar el producto:
$$ (a+b)^2 = (a+b)(a+b)= $$
$$ = a \cdot a + a \cdot b + $$
$$ + b \cdot a + b\cdot b = $$
$$ a^2 +2ab +b^2 $$
Cuadrado de la resta
$$(a - b)^2 = a^2- 2ab +b^2$$
Ejemplo:
$$ (x-2)^2 = x^2 -4x +4 $$
Ver demostración
La demostración es similar a la de la suma:
$$ (a-b)^2 = (a-b)(a-b)= $$
$$ = a \cdot a + a \cdot (-b) + $$
$$ + (-b) \cdot a + (-b)\cdot (-b) = $$
$$ a^2 -2ab +b^2 $$
Cubo de la suma
$$(a + b)^3 = a^3 + 3a^2b +3ab^2+ b^3$$
Ejemplo:
$$ (x+2)^3 = x^3 +6x^2 + 12x +8 $$
Ver demostración
Desarrollamos el producto, pero para agilizar los cálculos, usaremos la fórmula
del cuadrado:
$$ (a+b)^3 = (a+b)^2(a+b) = $$
$$ =(a^2 +2ab + b^2) (a+b) = $$
$$ = a^3 +2a^2b + ab^2 + $$
$$ + a^2b + 2ab^2 + b^3 = $$
$$ = a^3 + 3a^2b + 3ab^2 +b^3 $$
Cubo de la resta
$$(a - b)^3 = a^3 - 3a^2b+3ab^2-b^3$$
Ejemplo:
$$ (x-5)^3 = x^3 -15x^2 +75x -125 $$
Ver demostración
Es similar a la de la suma:
$$ (a-b)^3 = (a-b)^2(a-b) = $$
$$ =(a^2 -2ab + b^2) (a-b) = $$
$$ = a^3 -2a^2b + ab^2 + $$
$$ - a^2b + 2ab^2 - b^3 = $$
$$ = a^3 - 3a^2b + 3ab^2 - b^3 $$
Truco para calcular los cubos
Si olvidamos la fórmula para la suma o la resta al cubo podemos
descomponer el cubo como un producto:
$$ (a+b)^3 = (a+b)^2 \cdot (a+b) $$
$$ (a-b)^3 = (a-b)^2 \cdot (a-b) $$
3. Identidades de Lagrange
Vamos a ver las identidades de Lagrange para binomios.
En realidad, estas identidades son muy fáciles de obtener, como veremos
en las demostraciones, pero si conocemos las fórmulas, que son muy
sencillas, podremos acelerar el proceso de cálculo.
Para binomios, las identidades de Lagrange son las siguientes:
$$(a^2+ b^2)\cdot (x^2+y^2) =$$
$$ =(ax + by)^2+(ay - bx)^2$$
Ejemplo:
$$ (z^2 + 2^2)(z^2+3^2) =$$
$$ =(z^2 + 6)^2 + (3z-2z)^2 $$
Hemos identificado a = z ,
b = 2 , x = z ,
y = 3.
Ver demostración
Lo que haremos desarrollar los productos:
$$ (a^2 + b^2 )\cdot (x^2 + y^2) = $$
$$ =^1 a^2 x^2+a^2 y^2+ $$
$$ +b^2 x^2+b^2 y^2= $$
$$ =^2 a^2 x^2+b^2 y^2+ $$
$$ +b^2 x^2+a^2 y^2= $$
$$ =^3 a^2 x^2+b^2 y^2+2axyb + $$
$$ +b^2 x^2+a^2 y^2-2axyb= $$
$$ =^4 (ax)^2+(by)^2+2(ax)(by) + $$
$$ +(bx)^2+(ay)^2-2(ay)(bx)= $$
$$ =^5 (ax+by)^2+(ay-bx)^2 $$
En la primera igualdad hemos desarrollado el producto de las sumas.
En la segunda igualdad hemos intercambiado el orden de los
sumandos segundo y cuarto.
En la tercera igualdad hemos sumado y restado 2axby. Esto no
afecta a la suma ya que sumar y restar el mismo número es lo mismo que
sumar 0. Estos términos corresponden a los sumandos tercero y sexto.
En la cuarta igualdad hemos escrito paréntesis en todos los
términos para que sea más intuitiva la forma de cada uno de los términos. De
este modo, la primera línea corresponde con el desarrollo del
producto de una suma y la segunda con el del producto de una resta.
$$(a^2- b^2 )\cdot(x^2- y^2) =$$
$$=(ax + by)^2- (ay + bx)^2$$
Ejemplo:
$$ (z^2 - 2^2)(z^2 - 3^2)=$$
$$ =(z^2 + 6)^2 - (3z+2z)^2 $$
Hemos identificado a = z ,
b = 2 , x = z ,
y = 3.
Ver demostración
La demostración es similar a la anterior:
$$ (a^2-b^2 )(x^2-y^2 )= $$
$$ = a^2 x^2-a^2 y^2+ $$
$$ -b^2 x^2+b^2 y^2= $$
$$ = a^2 x^2+b^2 y^2+ $$
$$ -b^2 x^2-a^2 y^2= $$
$$ = a^2 x^2+b^2 y^2+2axyb+ $$
$$ -b^2 x^2-a^2 y^2-2axyb= $$
$$ = (ax)^2+(by)^2+2(ax)(by)+ $$
$$ -((bx)^2+(ay)^2+2(ay)(bx) )= $$
$$ = (ax+by)^2-(ay+bx)^2 $$
4. Completación de cuadrados
La completación de cuadrados es un procedimiento matemático que
se utiliza cuando se necesita expresar un trinomio de segundo grado en la suma de un
cuadrado y un número. Esto resuelta útil para simplificar expresiones algebraicas.
Si tenemos el trinomio
$$ ax^2 + bx + c,\ a \neq 0 $$
Entonces, podemos escribirlo como
$$ a(x+h)^2+k $$
Para ello tenemos que dar los valores
$$ h = \frac{b}{2a}, \ k = c-ah^2 $$
Ejemplo:
$$ 2x^2 + 3x + 1 = 2\left( x+ \frac{3}{4} \right)^2- \frac{1}{8} $$
Ver demostración
Queremos que se cumpla la igualdad
$$ ax^2 + bx + c = a(x+h)^2+k $$
Desarrollamos el binomio al cuadrado del lado derecho de la igualdad:
$$ ax^2 + bx + c =a(x+h)^2+k = $$
$$ = ax^2 + ah^2 + 2axh + k = $$
$$ = ax^2 + (2ah)x + (k+ah^2 ) $$
En la última igualdad sólo hemos reescrito la expresión anterior
agrupando el orden de los sumandos para ver más
fácilmente que necesitamos que
$$ 2ah=b \rightarrow h= b/2a $$
$$ k+ah^2=c \rightarrow k=c-ah^2 $$
5. Ejercicios resueltos
1. Suma por diferencia
Ejercicio 1
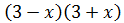
Solución
Ejercicio 2
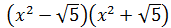
Solución
Recordemos que al elevar al cuadrado una raíz cuadrada ésta desaparece:
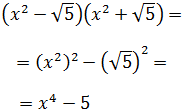
Ejercicio 3
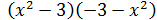
Solución
Tal como está escrita la expresión no parece que sea una suma por una
diferencia, pero sí si extraemos como factor común el signo negativo:
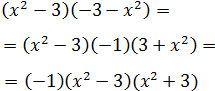
En la igualdad anterior hemos cambiado el orden de los factores,
lo cual no afecta al producto.
Ahora ya tenemos una suma por diferencia:
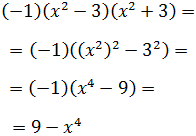
Ejercicio 4
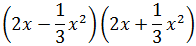
Solución
Recordemos que al elevar una fracción a una potencia, elevamos a dicha potencia el
numerador y el denominador:
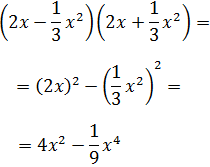
Notemos que los sumandos son productos: uno es
$$ 2x $$
y el otro es
$$ \pm \frac{x^2}{3} $$
Por tanto, al elevar al cuadrado hemos aplicado la propiedad de la potencia
del producto.
Ejercicio 5
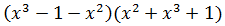
Solución
Aparentemente no tenemos una suma por diferencia ya que hay tres sumandos,
pero podemos reescribir la expresión agrupando los sumandos para que tenga
la forma deseada:
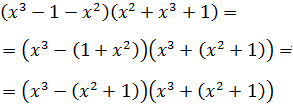
Notemos que hemos agrupado dos de los sumandos para considerarlo como un sólo sumando.
Que podemos hacer esta agrupación se debe a la propiedad asociativa de
la suma:
$$ a + (b + c ) = ( a + b) + c = a+b+c $$
Ahora calculamos el producto suma por diferencia, pero teniendo en cuenta que
uno de los sumandos que tenemos que elevar al cuadrado es un paréntesis:
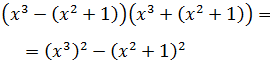
El segundo término es el cuadrado de una suma,
por lo que tendremos que aplicar la fórmula del binomio de Newton:
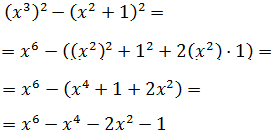
Ejercicio 6 (dificultad alta)
Obtener una ecuación de segundo grado
(en la que no aparecen números complejos) pero que tenga las soluciones complejas
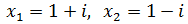
Solución
Puesto que x 1 y x 2 son las raíces de la ecuación,
una factorización de la misma es
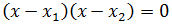
es decir,
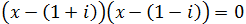
No queremos que aparezcan números complejos, así que tendremos que deshacernos
de la unidad imaginaria.
Notemos que podemos reescribir la expresión como una suma por diferencia:
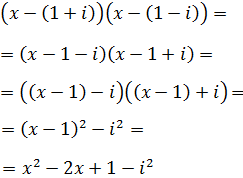
Como
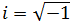
Entonces su cuadrado es
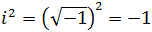
Por tanto,
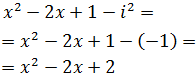
Luego la ecuación de segundo grado que encontramos es
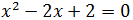
Ejercicio 7
Resolver, usando la fórmula de suma por diferencia, la ecuación de sexto
grado siguiente:
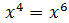
Solución
Podemos extraer factor común en la ecuación:
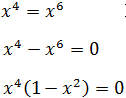
Uno de los factores es la diferencia de dos cuadrados:
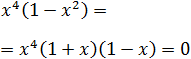
Tenemos factorizada la ecuación y de esta expresión podemos deducir las soluciones:
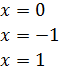
La primera solución (x = 0) es de multiplicidad 4 y las otras dos
son simples (multiplicidad 1).
Nota: la multiplicidad es el
grado del factor del cuál la raíz es también raíz (por ejemplo, la solución 0 es raíz del factor
x 4, por lo que tiene multiplicidad 4.
Ejercicio 8
Simplificar la siguiente fracción:
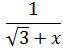
Solución
Hay un convenio entre los matemáticos de no escribir raíces cuadradas en el denominador,
aunque a veces esto supone que la expresión sea más compleja que la inicial, como
ocurre en esta fracción.
Lo que haremos es multiplicar el numerador y el denominador por el mismo número.
Esto es lo mismo que multiplicar la fracción por 1, por lo que sigue siendo la misma.
La única forma de que la raíz desaparezca es multiplicándola por ella misma, es decir,
elevarla al cuadrado.
En el denominador tenemos una suma. Si la multiplicamos por la diferencia, tendremos
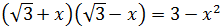
Lo hacemos en la fracción:
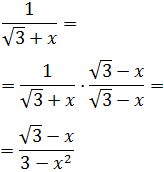
Ejercicio 9
Calcular la siguiente suma de fracciones y simplificar el resultado:
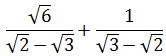
Solución
Tenemos que sumar las fracciones y luego, evitar las raíces en el denominador.
Si nos fijamos, los denominadores son los mismos pero de signo contrario:
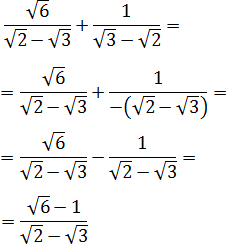
Ahora multiplicamos y dividimos por la suma de las
raíces para tener una suma por diferencia:
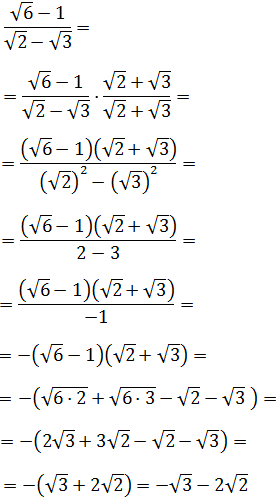
2. Binomios al cuadrado y al cubo
Ejercicio 1
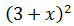
Solución
Ejercicio 2
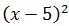
Solución
Ejercicio 3
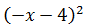
Solución
Todos los signos son negativos, por lo que podemos extraer -1 como factor común,
obteniendo así una suma al cuadrado:
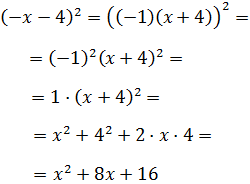
Notemos que tenemos el cuadrado de un producto y que al elevar al cuadrado el signo
negativo desaparece.
Ejercicio 4
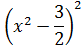
Solución
En este binomio, el primer sumando ya está al cuadrado y el segundo es una fracción.
Al elevar al cuadrado la fracción tenemos que elevar al cuadrado el numerador y el
denominador:
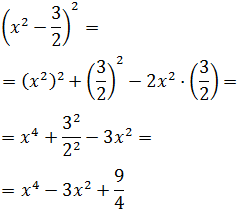
Ejercicio 5
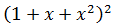
Solución
Se trata de un trinomio al cuadrado. Lo que
haremos es escribir la suma como un binomio, siendo uno de los sumandos un binomio.
Para ello agrupamos dos de los sumandos con paréntesis:
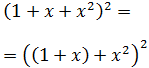
Ahora tiene la forma de un binomio al cuadrado, pero tendremos que aplicar dos veces la fórmula:
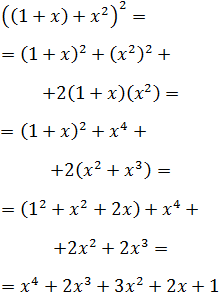
Ejercicio 6
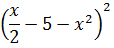
Solución
De nuevo tenemos un trinomio al cuadrado: agrupamos dos sumandos para tener la forma
de un binomio al cuadrado y poder aplicar la fórmula:
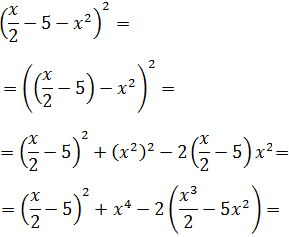
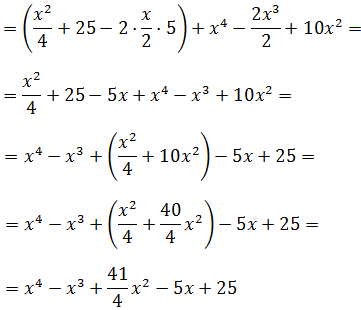
Ejercicio 7
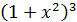
Solución
Tenemos que aplicar la fórmula de la suma al cubo:
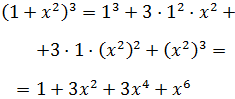
Recordemos que podemos descomponer el cubo si no recordamos la fórmula:
$$ (a+b)^3 = (a+b)^2 \cdot (a+b) $$
Ejercicio 8
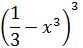
Solución
Aplicamos la fórmula de la resta al cubo:
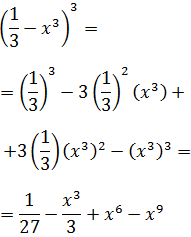
3. Identidades de Lagrange
En todos los ejercicios, escribir el producto como suma (o resta) de cuadrados:
Ejercicio 1
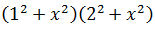
Solución
Ejercicio 2
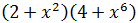
Solución
Para aplicar la identidad de Lagrange tenemos que escribir los sumandos como
cuadrados:
El 2 lo podemos escribir como una raíz cuadrada al cuadrado:
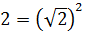
El 4 es 2 al cuadrado y x 6 lo podemos escribir como
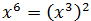
Por tanto,
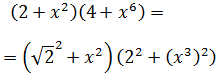
Ahora ya podemos aplicar la fórmula:
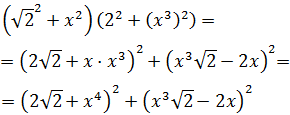
Ejercicio 3
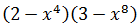
Solución
Tenemos que escribir cada sumando como un cuadrado:
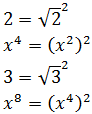
Por tanto,
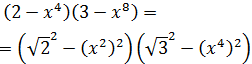
Finalmente aplicamos la fórmula:
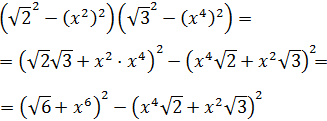
4. Completación de cuadrados
En todos los ejercicios, completar los cuadrados
sin utilizar las fórmulas anteriores para
calcular a, h y k.
Ejercicio 1
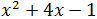
Solución
Desarrollamos la expresión que queremos obtener:
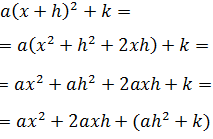
En la última igualdad sólo hemos agrupado los términos para ver
rápidamente que el primero se caracteriza por tener
x al cuadrado, el segundo por tener x
(sin estar al cuadrado) y el tercero
(es el paréntesis) no tiene ninguna x.
Ahora igualamos los términos de la expresión inicial
con los de la obtenida según tengan o no la x (al cuadrado o no):
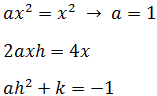
De la primera igualdad hemos deducido que a = 1.
Nota: aunque estamos acostumbrados a que x sea la incógnita,
en estas ecuaciones no lo es. Las incógnitas son a, h y k.
Ahora sustituimos el valor de a en las otras dos ecuaciones:
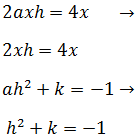
En la primera igualdad pasamos el 2 dividiendo a la derecha:
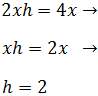
Tenemos la h y la sustituimos en la igualdad que nos queda:
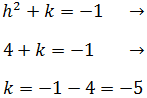
Por tanto, tenemos que
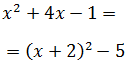
Ejercicio 2
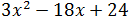
Solución
Desarrollamos la expresión a la que queremos llegar para obtener las ecuaciones:
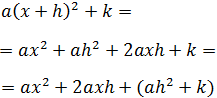
Tenemos tres ecuaciones:
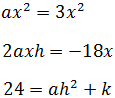
Nota: los signos negativos hay que escribirlos también.
Resolvemos la primera ecuación:
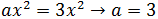
Resolvemos la segunda:
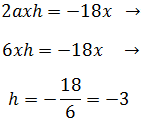
Y finalmente la tercera:
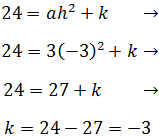
Por tanto,
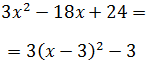
Ejercicio 3
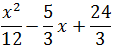
Solución
Al igual que en los ejercicios anteriores
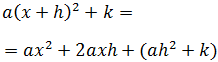
De donde obtenemos las ecuaciones:
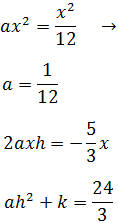
Resolvemos la segunda ecuación:
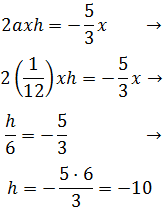
Y la última:
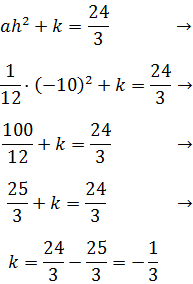
Por tanto,
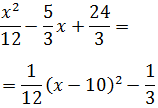
Ejercicio 4
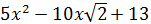
Solución
En este trinomio tenemos una raíz cuadrada, pero el procedimiento sigue siendo el mismo:
Al igual que en los ejercicios anteriores:
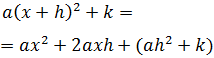
Por tanto, queremos que
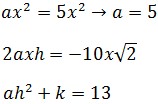
Resolvemos la segunda ecuación:
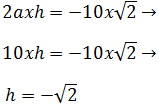
Y la tercera:
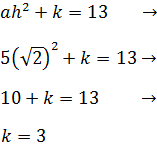
Por tanto,
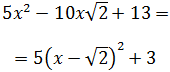
Ejercicio 5
Se desea escribir el polinomio
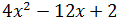
en la forma
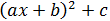
de modo que a, b y c sean números sin la incógnita x.
Encontrar las dos únicas posibilidades.
Solución
En este problema la forma que se nos pide es distinta a los anteriores.
Desarrollamos la expresión que queremos obtener y luego identificaremos los términos:
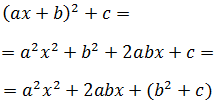
Identificamos los términos:
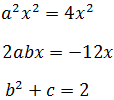
La primera ecuación es de segundo grado ya que
tenemos a 2.
Las dos posibles soluciones son:
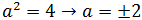
Ahora usaremos a = 2 y luego que a = -2 para obtener las dos
formas que se piden:
Resolvemos la segunda ecuación (a = 2):
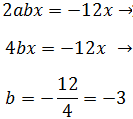
Y la tercera:
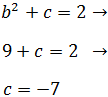
Ahora hacemos lo mismo pero con a = -2:
En la segunda ecuación:
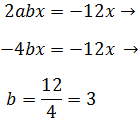
Y en la tercera:
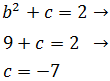
Por tanto, las dos formas que se piden son
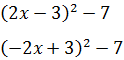
Nota: que haya dos posibilidades se debe a que
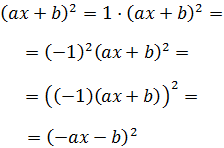
Es decir, como tenemos un cuadrado,
podemos cambiar el signo a todos los
elementos del paréntesis sin que se
modifique el resultado.



Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.