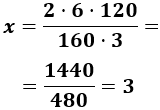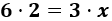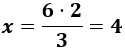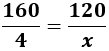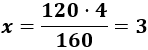1. Método de resolución
Explicaremos el método a medida que resolvemos el siguiente problema:
Problema: si 6 niños comen 160 caramelos en 2 horas, ¿cuántas horas tardan 3 niños en comer 120 caramelos?
-
Distinguir las tres variables:
Las variables del problema son:
-
(número de) niños
-
(número de) caramelos
-
(número de) horas
Una de las tres variables es la variable incógnita.
Nuestra variable incógnita es horas.
-
Estudiar el tipo de proporcionalidad de cada una de las variables con la variable incógnita.
Como la variable incógnita es horas, estudiamos la relación entre las variables niños y horas y las variables caramelos y horas:
-
Niños-horas: cuantos más niños hay, menos horas tardan en comer los caramelos. Es una proporcionalidad inversa.
-
Caramelos-horas: cuantos más caramelos hay, más horas tardan en comerlos. Es una proporcionalidad directa.
Escribimos los datos en una tabla:
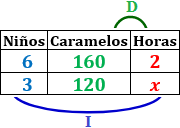
Escribiremos la variable incógnita en la columna de la derecha e indicamos con flechas si se trata de una proporcionalidad directa (D) o inversa (I).
Tenemos que calcular el valor de la incógnita \(x\).
-
Calculamos la regla de tres compuesta:
Escribimos las dos columnas de la izquierda como dos fracciones que se multiplican e igualamos con la columna derecha:

Importante:
si es una proporcionalidad directa, escribimos la primera fila dividido entre la segunda.
-
si es una proporcionalidad inversa, escribimos la segunda fila dividido entre la primera.
-
Calculamos la incógnita \(x\):
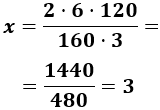
Por tanto, 3 niños tardan 3 horas en comer 120 caramelos.
2. Problemas resueltos
Problema 1
Si con 4 grifos de agua cuyas bocas de salida son de 2cm2 se obtienen 300 litros en un determinado tiempo, ¿cuántos litros se obtienen en el mismo tiempo con 2 grifos con bocas de 3cm2?
Solución
Variables: número de grifos, área y litros.
Variable incógnita: litros.
Relación entre las variables:
Grifos-Litros: cuantos más grifos se emplean, más litros se obtienen. Es una proporcionalidad directa.
-
Área-Litros: cuanto mayor sea el área de las bocas de los grifos, más litros se obtienen. Es una proporcionalidad directa.
Tabla con los datos:
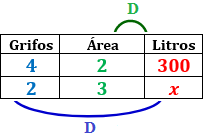
Calculamos una regla de tres compuesta:
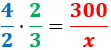
Despejamos la variable incógnita:
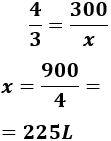
Por tanto, se obtienen 225 litros de agua con 2 grifos con bocas de 3cm2.
Solución
Problema 2
Se sabe que 6 mangueras abiertas durante 3 horas equivalen a 10.000 litros. ¿Cuánto tiempo se necesita para llenar una piscina de 130.000 litros con 4 de estas mangueras?
Solución
Variables: cantidad de mangueras, litros y horas.
Variable incógnita: horas.
Relación entre las variables:
-
Mangueras-Horas: Cuantas más mangueras, menos horas se necesitan. Es una proporcionalidad inversa.
Litros-Horas: Cuantos más litros de agua, más horas se necesitan. Es una proporcionalidad directa.
Tabla con los datos:
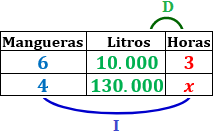
Calculamos una regla de tres compuesta:

Despejamos la variable incógnita:
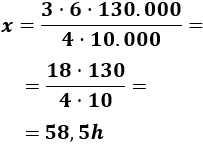
Por tanto, se necesitan 58 horas y media para llenar la piscina.
Solución
Problema 3
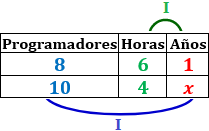
Un equipo de 8 programadores trabajará 6 horas diarias para desarrollar un software en un año. Si se forma un equipo de 10 programadores trabajando 4 horas diarias, ¿cuántos años se necesitan para realizar un proyecto de la misma envergadura?
Solución
Variables: número de programadores, número de horas diarias y número de años.
Variable incógnita: años.
Relación entre las variables:
-
Programadores-Años: Cuantos más programadores, menos años. Es una proporcionalidad inversa.
-
Horas-años: Cuantas más horas diarias, menos años. Es una proporcionalidad inversa.
Tabla con los datos:
Calculamos una regla de tres compuesta:
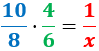
Despejamos la variable incógnita:
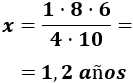
Por tanto, se necesitarán 1,2 años
Solución
Problema 4
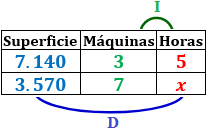
El estadio Azteca de la Ciudad de México tiene una superficie de 7.140 metros cuadrados. Para cortar su césped se emplean 3 máquinas cortacésped funcionando durante 5 horas. ¿Cuánto tiempo se requiere para cortar el césped de un estadio cuya superficie sea la mitad si se emplean 7 máquinas?
Solución
Variables: superficie, número horas y número de máquinas.
Variable incógnita: horas.
Relación entre las variables:
Superficie – Horas: Cuanto mayor es la superficie, más horas se tarda. Es una proporcionalidad directa.
Máquinas – Horas: Cuantas más máquinas se utilicen, menos horas se tarda. Es una proporcionalidad inversa.
Tabla con los datos:
Calculamos una regla de tres compuesta:
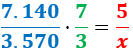
Despejamos la variable incógnita:

Por tanto, se necesitan 1,07 horas. Es decir, 1 hora, 4 minutos y 12 segundos.
Solución
Problema 5
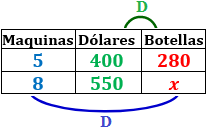
Una compañía dispone de 5 máquinas de refresco que llenan 280 botellas que se venden por un total de 400 dólares. Si la compañía compra 3 nuevas máquinas embotelladoras para ganar un total de 550 dólares, ¿cuántas botellas deben llenar?
Solución
Variables: número de horas, número de botellas y cantidad de dólares.
Variable incógnita: botellas.
Relación entre las variables:
Máquinas – Botellas: cuantas más máquinas, más botellas se llenan. Es una proporcionalidad directa.
-
Dólares – Botellas: cuantos más dólares se ganan, más botellas se llenan. Es una proporcionalidad directa.
Tabla con los datos:
Calculamos una regla de tres compuesta:
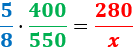
Despejamos la variable incógnita:

Por tanto, deben llenarse 616 botellas.
Solución
Problema 6
John y Paul tienen una banda y componen 6 canciones en 15 días. Si llaman a su amigo George para que les ayude durante 5 días, ¿cuántas canciones compondrán?
Solución
Variables: número de personas, número de días y número de canciones.
Variable incógnita: número de canciones.
Relación entre las variables:
-
Personas – canciones: cuantas más personas, más canciones componen. Es una proporcionalidad directa.
-
Días – canciones: cuantos más días, más canciones. Es una proporcionalidad directa.
Tabla con los datos:
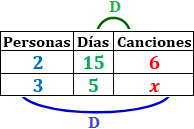
Calculamos una regla de tres compuesta:
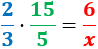
Despejamos la variable incógnita:
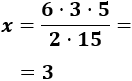
Por tanto, compondrán 3 canciones.
Solución
Problema 7
Un atleta corrió 2 horas diarias durante 30 días y adelgazó 5 kilos. Si corriera solamente 20 días, pero lo hiciera por 3 horas, ¿cuántos kilos perdería?
Solución
Variables: número de horas, número de kilos y número de días.
Variable incógnita: kilos.
Relación entre las variables:
Horas -Kilos: cuantas más horas corra, más kilos pierde. Es una proporcionalidad directa.
Días -Kilos: cuantos más días corre, más kilos pierde. Es una proporcionalidad directa.
Tabla con los datos:
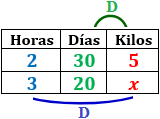
Calculamos una regla de tres compuesta:
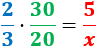
Despejamos la variable incógnita:
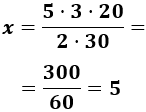
Por tanto, perdería el mismo número de kilos.
Solución
Problema 8
Cuatro empleadas de una tienda de moda tardan 8 días en coser 6 vestidos. Calcular cuánto tiempo se necesita para coser 24 vestidos si se duplica la plantilla.
Solución
Variables: número de empleadas, número de días y número de vestidos.
Variable incógnita: días.
Relación entre las variables:
-
Empleadas-Días: cuantas más empleadas, menos días se necesitan. Es una proporcionalidad inversa.
Vestidos-Días: cuantos más vestidos se cosen, más días se necesitan. Es una proporcionalidad directa.
Tabla con los datos:
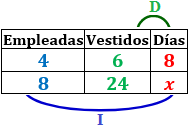
Calculamos una regla de tres compuesta:
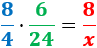
Despejamos la variable incógnita:
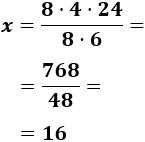
Por tanto, se necesita duplicar la plantilla durante 16 días.
Solución
Problema 9
Un buque de carga realiza un transporte en 24 días con tan solo 3 motores encendidos con un consumo total de 2.000L de fuel. Si se encienden sus 6 motores para realizar un transporte con un consumo total de 3.000L, ¿cuánto dura el transporte?
Solución
Variables: número de motores, número de días y cantidad de fuel.
Variable incógnita: días.
Relación entre las variables:
Motores-Días: cuantos más motores, menos días se necesitan. Es una proporcionalidad inversa.
Fuel – Días: cuanto más fuel se consume, más días se navega. Es una proporcionalidad directa.
Tabla con los datos:
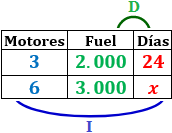
Calculamos una regla de tres compuesta:
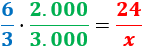
Despejamos la variable incógnita:

Por tanto, el transporte dura 18 días.
Solución
Problema 10
Un novelista que escribe 15 páginas en 90 minutos a una velocidad de 22 palabras por minuto necesita escribir 10 páginas cada 75 minutos para terminar su libro dentro del plazo. ¿Cuántas palabras por minuto debe escribir? ¿Cuántas palabras tiene una página?
Solución
Variables: número de minutos, número de páginas y velocidad.
Variable incógnita: velocidad.
Relación entre las variables:
-
Páginas-Velocidad: cuantas más páginas escribe, mayor debe ser la velocidad. Es una proporcionalidad directa.
-
Minutos-Velocidad: cuantos más minutos escribe, menor debe ser la velocidad. Es una proporcionalidad inversa.
Tabla con los datos:

Calculamos una regla de tres compuesta:
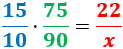
Despejamos la variable incógnita:

Por tanto, debe escribir a una velocidad de 17,6 palabras por minuto.
Calculamos las palabras por página:
Si la velocidad es 22 palabras por minuto, el número de palabras que escribe en 90 minutos es
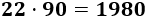
Y como sabemos que en 90 minutos escribe 15 páginas, el número de palabras por página es
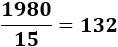
Solución
Problema 11
El año pasado, una empresa cubana de producción de azúcar contrató 20 operarios que recolectaron al día una media de 100kg de caña por persona en dos semanas de recolecta. Calcular cuántos operarios deben contratar este año para que en una semana recolecten 2.000 kilos en total.
Solución
Variables: número de kilos (totales), número de días y número de operarios.
Variable incógnita: número de operarios.
Relación entre las variables:
-
Kilos-Operarios: cuantos más kilos se recolectan en total, más operarios se requieren. Es una proporcionalidad directa.
-
Tiempo-Operarios: cuanto más tiempo dura la recolecta, menos operarios se necesitan. Es una proporcionalidad inversa.
Tabla con los datos:
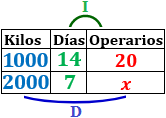
Calculamos una regla de tres compuesta:

Despejamos la variable incógnita:

Por tanto, este año deben contratar 80 operarios.
Nota: se necesita el cuádruple de operarios ya que se quiere recolectar el doble de kilos en la mitad de tiempo.
Solución
Problema 12
Una empresa cuenta con un equipo de 3 técnicos que pueden reparar los 6 elevadores del edificio en tan solo 180 minutos en caso de avería. Si se necesita reparar 5 elevadores, pero uno de los técnicos no podrá asistir, ¿cuánto tiempo tardarán en repararlos?
Solución
Variables: número de técnicos (disponibles), número de elevadores (averiados) y tiempo (en minutos).
Variable incógnita: tiempo (minutos).
Relación entre las variables:
Técnicos-Tiempo: cuantos más técnicos, menos tiempo tardan en reparar. Es una proporcionalidad inversa.
Elevadores-Tiempo: cuantos más elevadores (averiados), más tiempo tardan en repararse. Es una proporcionalidad directa.
Tabla con los datos:
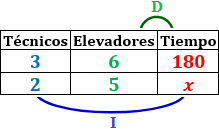
Calculamos una regla de tres compuesta:
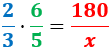
Despejamos la variable incógnita:
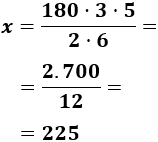
Por tanto, tardarán 225 minutos en reparar los 5 elevadores.
Solución
Problema 13
Para construir una casa en 6 meses (183 días), un arquitecto estimó que serían necesarios 16 obreros trabajando 10 horas al día. Sin embargo, limitado por el presupuesto, se decidió por contratar solamente a 8 obreros trabajando 6 horas diarias.
¿Cuánto tiempo durará la construcción?
Solución
Variables: número de obreros, número de horas diarias y número de días.
Variable incógnita: días.
Relación entre las variables:
Obreros-días: cuantos más obreros, menos días tardan en construir la casa. Es una proporcionalidad inversa.
Horas-días: cuantas más horas al día trabajan, menos días tardan en construir la casa. Es una proporcionalidad inversa.
Tabla con los datos:
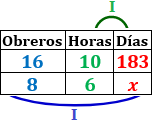
Calculamos una regla de tres compuesta:
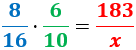
Despejamos la variable incógnita:
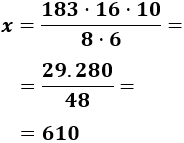
Por tanto, tardarán 610 días en construir la casa. Es decir, aproximadamente 1 año y 8 meses.
Solución
Problema 14
En un sembradío de sandías que es regado 2 veces a la semana se podrían cosechar 12 toneladas de esta fruta en 4 meses. Sin embargo, se riega 4 veces semanales para duplicar la producción. ¿Cuántas toneladas se producen en tres meses?
Solución
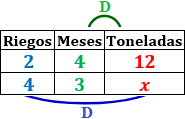
Variables: número de riegos semanales, número de toneladas de sandía y número de meses.
Variable incógnita: toneladas.
Relación entre las variables:
Riegos-Toneladas: cuanto más se riega, más toneladas se producen. Es una proporcionalidad directa.
-
Meses-Toneladas: cuantos más meses pasan, más toneladas se producen. Es una proporcionalidad directa.
Tabla con los datos:
Calculamos una regla de tres compuesta:
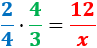
Despejamos la variable incógnita:
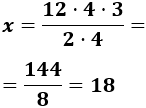
Por tanto, se producen 18 toneladas en tres meses si se duplica el riego.
Solución
Problema 15
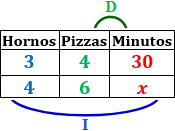
Alberto y Gabriel son dueños de sendas pizzerías. En la de Gabriel se cocinan 4 pizzas en 3 hornos en 30 minutos. Si Alberto dispone de 4 hornos, ¿cuanto tardará en cocinar 6 pizzas suponiendo que ambos manejan el mismo tipo de horno?
Solución
Variables: número de hornos, número de pizzas y tiempo (en minutos).
Variable incógnita: minutos.
Relación entre las variables:
Hornos-tiempo: cuantos más hornos se manejan, menos tiempo se requiere. Es una proporcionalidad inversa.
Pizzas-tiempo: cuantas más pizzas se cocinan, más tiempo se requiere. Es una proporcionalidad directa.
Tabla con los datos:
Calculamos una regla de tres compuesta:
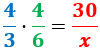
Despejamos la variable incógnita:
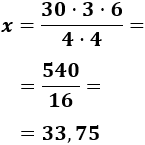
Por tanto, Alberto tardará 33,75 minutos. Es decir, 33 minutos y 45 segundos.
Solución
3. Explicación extensa
En el apartado 1 (método de resolución) hemos resuelto un problema aplicando una regla de tres compuesta, pero no hemos explicado por qué se calcula así la regla de tres.
En esta sección volveremos al problema para resolverlo aplicando dos reglas de tres simples. Este procedimiento puede abreviarse haciendo los cálculos explicados en el apartado 1.
Recordamos el problema:
Si 6 niños comen 160 caramelos en 2 horas, ¿cuántas horas tardan 3 niños en comer 120 caramelos?
La tabla con los datos del problema es:

Paso 1:
La relación de proporcionalidad entre niños y horas es inversa.
Si 6 niños tardan 2 horas, ¿cuánto tardan 3 niños?
Calculamos una regla de tres simple (inversa):
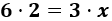
Por tanto, \(x\) es
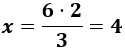
Por tanto, 3 niños tardan 4 horas en comer 160 caramelos.
Nosotros queremos saber cuánto tardan en comer sólo 120 caramelos.
Paso 2:
La relación de proporcionalidad entre horas y caramelos es directa.
Si los 3 niños tardan 4 horas en comer 160 caramelos, ¿cuánto tardan en comer 120 caramelos?
Calculamos una regla de tres simple (directa):
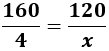
Por tanto, \(x\) es
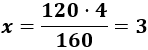
Por tanto, 3 niños tardan 3 horas en comer 120 caramelos.