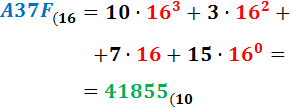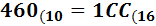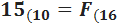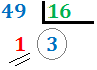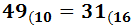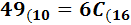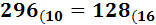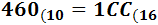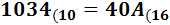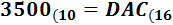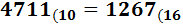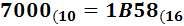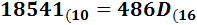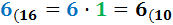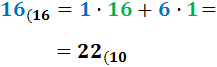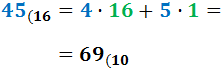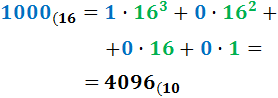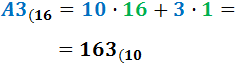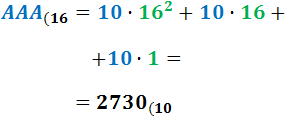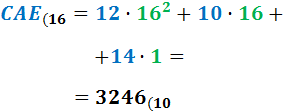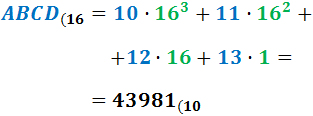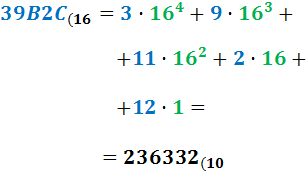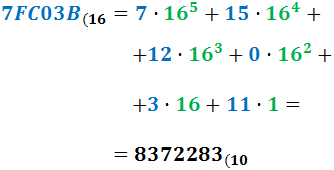Sistema de Numeración Hexadecimal
(Base 16)
Contenido de esta página:
-
Introducción
-
Cambio de base 10 a base 16 (método)
-
Cambio de base 16 a base 10 (método)
-
20 Ejercicios Resueltos: diez ejercicios de cambio de base
16 a base 10 y diez de cambio de base 10 a base 16.
Introducción
Ya mencionamos en el tema del sistema de numeración octal
que, aunque el sistema de numeración decimal es el más usado, hay otros sistemas que también son de mucha importancia. Éste era el caso del sistema octal y también es el del sistema de numeración hexadecimal (en base 16).
El sistema hexadecimal es un sistema de numeración posicional de base 16.
Los símbolos que se usan en este sistema son:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
Para indicar que un número está escrito en base 16, usamos
el subíndice \(_{(16}\) (o el subíndice \(_{hex}\)),
y para indicar que un número está escrito en base 10,
usamos el subíndice \(_{(10}\).
Ejemplos:
-
\( 4_{(16} = 4_{(10} \)
-
\( 20_{(16} = 32_{(10} \)
-
\( A3_{(16} = 163_{(10} \)
-
\( 1CC_{hex} = 460_{(10} \)
Observación:
El sistema hexadecimal sólo utiliza los dígitos del 0 al 9 y las letras de la A a la F, con lo que los siguientes números NO están bien expresados:
-
\( 1G_{(16} \)
-
\( HH_{(16} \)
-
\( X3_{(16} \)
-
\( 12A_{(16} \)
-
\( 2129_{(16} \)
Para pensar:
Tenemos un número escrito en base 8. Si queremos pasarlo al sistema hexadecimal, ¿puede que necesitemos usar menos cifras que en el sistema hexadecimal?
Tenemos un número escrito en base 10. Si queremos pasarlo al sistema hexadecimal, ¿puede que necesitemos usar menos cifras que en el sistema decimal?
¿Podríamos definir el sistema hexadecimal usando las letras U, V, W, X, Y, Z en vez de las letras A, B, C, D, E, F? ¿Y sustituyendo A,B,C,D,E,F por 10, 11, 12, 13, 14, 15?
Cambio de base decimal/hexadecimal
A continuación, explicamos cómo pasar un número del sistema
decimal al sistema hexadecimal, y viceversa.
Cambio de base 10 a base 16
Ver método
Veamos el método para pasar del sistema
decimal al sistema hexadecimal mediante un ejemplo.
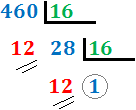
Escribiremos el número \(460_{(10}\) (base 10) en base 16:
-
Dividimos el número entre 16:
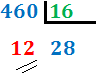
-
Si el cociente es mayor o igual que 16, lo dividimos entre 16.
En nuestro caso, el cociente es 28 (mayor que 16), con lo que lo dividimos
de nuevo:

-
Continuamos así hasta obtener un cociente menor que 16.
En nuestro caso, el cociente es 1 (menor que 16), con lo que hemos terminado el proceso. Hemos indicado los restos con dos rayas y el último cociente con una circunferencia.
-
El número en base 16 es:
(Último cociente) (Último resto) (Penúltimo resto)... (Segundo resto)
(Primer resto).
Teniendo en cuenta que: 10 es A,
11 es B,
12 es C, 13 es D, 14 es E
y 15 es F.
En nuestro caso,
El último cociente es 1.
-
El último resto es 12 (es decir, C).
-
El penúltimo resto es 12 (es decir, C).
El primer resto es 0.
Por tanto, el número 460 en base hexadecimal es 1CC. Es decir,
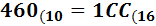
Cambio de base 16 a base 10
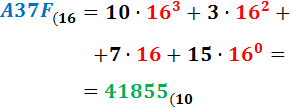
Ver método
El método que seguiremos para pasar un número en base hexadecimal a base
decimal es:
-
De derecha a izquierda: multiplicamos la primera
cifra por 1 (1 es 160); la segunda, por 16
(16 es 161); la tercera, por 162; la cuarta,
por 163. Y así hasta que hayamos
multiplicado todas las cifras.
Sumamos cada uno de los valores obtenidos.
Ejemplo: pasamos el número \(A37F_{(16}\) a base 10:
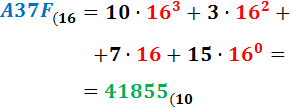
Ejercicios Resueltos de Cambio de Base
A. Cambio de base 10 a base 16
Escribir en base 16 los siguientes números
escritos en el sistema decimal (es decir, en base 10):
Ejercicio 1: \( 15_{(10} \)
Ver Solución
Como 15 es menor que 16, no es necesario dividirlo entre 16. El número en base 16 es F(16.
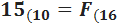
Ejercicio 2: \( 49_{(10} \)
Ver Solución
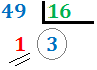
Dividimos 49 entre 16. Como el cociente,
3, es menor que 16,
hemos terminado. El número en base hexadecimal
es \( 31_{(16}\).
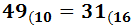
Ejercicio 3: \( 108_{(10} \)
Ver Solución
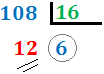
Dividimos 108 entre 16. Como el cociente,
6, es menor que 16,
hemos terminado. El número en base hexadecimal
es \( 6C_{(16}\).
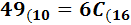
Ejercicio 4: \( 296_{(10} \)
Ver Solución
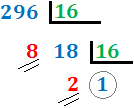
Dividimos 296 entre 16. Como el cociente,
18, es mayor que 16, lo dividimos entre 16. Como el segundo cociente, 1, es menor que 16, el proceso ha finalizado. El número en base hexadecimal
es \( 128_{(16}\).
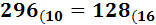
Ejercicio 5: \( 460_{(10} \)
Ver Solución
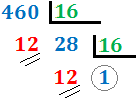
Dividimos 460 entre 16. Como el cociente,
28, es mayor que 16, lo dividimos entre 16. Como el segundo cociente, 1, es menor que 16, el proceso ha finalizado. El número en base hexadecimal
es \( 1CC_{(16}\).
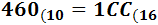
Ejercicio 6: \( 1034_{(10} \)
Ver Solución
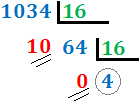
Dividimos 1034 entre 16. Como el cociente,
64, es mayor que 16, lo dividimos entre 16. Como el segundo cociente, 4, es menor que 16, el proceso ha finalizado. El número en base hexadecimal
es \( 40A_{(16}\).
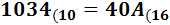
Ejercicio 7: \( 3500_{(10} \)
Ver Solución
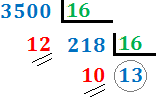
Como el cociente, 218, es mayor o igual que 16, volvemos a dividir, obteniendo el cociente 13, que es menor que 16. Hemos terminado el proceso y el número en base hexadecimal es \( DAC_{(16}\).
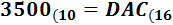
Ejercicio 8: \( 4711_{(10} \)
Ver Solución
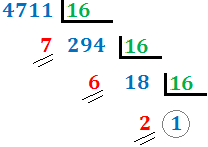
Como el cociente, 294, es mayor o igual que 16, volvemos a dividir, obteniendo el cociente 18, que también es mayor o igual que 16, con lo que volvemos a dividir. Obtenemos el cociente 1, que es menor que 16. Hemos terminado el proceso y el número en base hexadecimal es \( 1267_{(16}\).
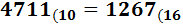
Ejercicio 9: \( 7000_{(10} \)
Ver Solución
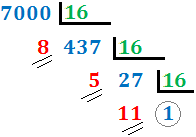
Como el cociente, 437, es mayor o igual que 16, volvemos a dividir, obteniendo el cociente 27, que también es mayor o igual que 16, con lo que volvemos a dividir. Obtenemos el cociente 11, que es menor que 16. Hemos terminado el proceso y el número en base hexadecimal es \( 1B58_{(16}\).
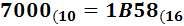
Ejercicio 10: \( 18541_{(10} \)
Ver Solución
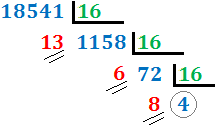
Como el cociente, 1158, es mayor o igual que 16, volvemos a dividir, obteniendo el cociente 72, que también es mayor o igual que 16, con lo que volvemos a dividir. Obtenemos el cociente 4, que es menor que 16. Hemos terminado el proceso y el número en base hexadecimal es \( 486_{(16}\).
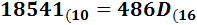
B. Cambio de base 16 a base 10
Escribir en base 10 los siguientes números
escritos en el sistema hexadecimal (es decir, en base 16):
Ejercicio 1: \( 6_{(16} \)
Ver Solución
Ejercicio 2: \( 16_{(16} \)
Ver Solución
Ejercicio 3: \( 45_{(16} \)
Ver Solución
Ejercicio 4: \( 1000_{(16} \)
Ver Solución
Ejercicio 5: \( A3_{(16} \)
Ver Solución
Ejercicio 6: \( AAA_{(16} \)
Ver Solución
Ejercicio 7: \( CAE_{(16} \)
Ver Solución
Ejercicio 8: \( ABCD_{(16} \)
Ver Solución
Ejercicio 9: \( 39B2C_{(16} \)
Ver Solución
Ejercicio 10: \( 7FC03B_{(16} \)
Ver Solución

Sistema de numeración hexadecimal -
(c) -
matesfacil.com

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.