Ecuaciones en Diferencias Finitas: Teoría |
Contenido de esta página:
Introducción
Definición de Ecuación en Diferencias Finitas
Soluciones de una EDF homogénea de primer orden
Soluciones de una EDF homogénea de segundo orden
Soluciones de una EDFH de orden k
Soluciones de una EDF no homogénea
1. Introducción
Las ecuaciones en diferencias finitas (EDF) son ecuaciones cuyas incógnitas son sucesiones, es decir, es una relación que cumplen los términos de una o varias sucesiones, con lo que su solución serán sucesiones. En esta sección mostramos un método para obtener las soluciones de una EDF, haciendo hincapié en las de primer y segundo orden.
Enlace: EDF resueltas.
Veremos que, al igual que ocurre en otro tipo de ecuaciones (como las EDP), tendremos que resolver primero la ecuación homogénea. Luego, a esta solución le sumamos una solución particular y obtendremos la solución de la ecuación completa (la no homogénea). Para las soluciones particulares, más difíciles de obtener, usaremos directamente una tabla de éstas en función del término independiente.
Respecto a sus aplicaciones, una de ellas es el estudio de la evolución de las variables temporales en Economía cuando se considera al tiempo como una variable discreta. Podemos encontrar más información sobre su utilidad y orígenes en el siguiente artículo de la Revista de métodos cuantitativos para la Economía y la Empresa que podemos encontrar en este enlace (PDF).
2. Definición de Ecuación en Diferencias Finitas
Llamamos EDF de orden k a la expresión
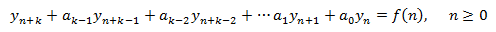
y diremos que la sucesión
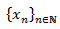
es una solución si verifica la EDF, es decir, si
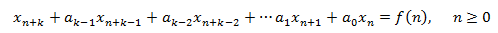
Se dice que la ecuación es homogénea (EDFH) si el término independiente es 0, esto es,
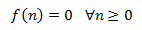
Se define el polinomio característico de la EDF
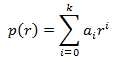
3. Soluciones de una EDF homogénea de primer orden
Una EDFH de primer orden es de la forma
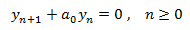
cuyo polinomio característico es
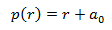
que tiene la única raíz
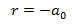
Veamos que la sucesión
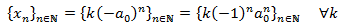
Es una solución de la EDF para todo k. Sustituyendo la sucesión en la EDF obtenemos
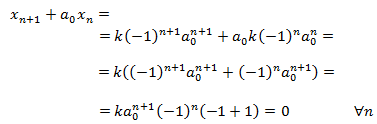
Llamamos solución general a la solución
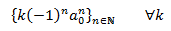
4. Soluciones de una EDF homogénea de segundo orden
Una EDFH de segundo orden es
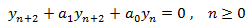
cuyo polinomio característico es
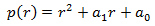
que es un polinomio de segundo grado. Distinguimos los siguientes casos:
- Dos raíces reales distintas
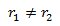
Las sucesiones
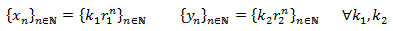
son soluciones de la EDF y, por tanto, su suma también. En efecto,
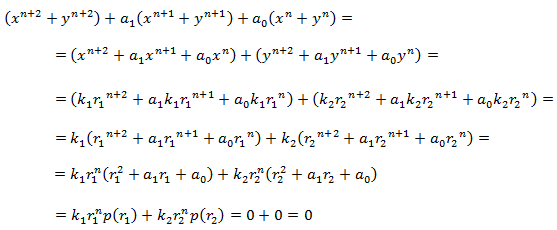
La solución general de la EDFH es
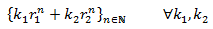
- Una raíz real de multiplicidad doble
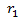
Análogamente al caso anterior se prueba que la siguiente sucesión es una solución de la EDF.
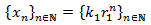
Ahora veamos que la sucesión
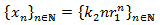
es solución y, por tanto, la suma de ambas también
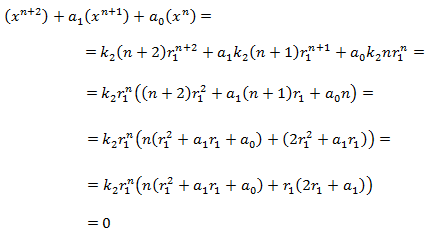
donde hemos usado que
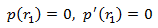
ya que
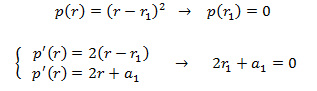
La solución general de la EDFH de segundo orden es
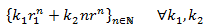
- Dos raíces complejas
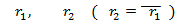
La sucesión
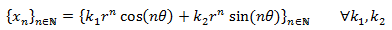
es solución de la EDFH, donde
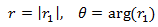
5. Soluciones de una EDFH de orden k
La EDFH es de la forma
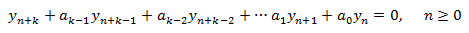
Si las raíces del polinomio característico son simples
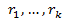
Tenemos que
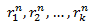
Forman una base del espacio de soluciones.
Si la multiplicidad de alguna raíz r es m>1, entonces
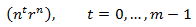
son soluciones de la EDF.
6. Soluciones de una EDF no homogénea
Tenemos la EDF
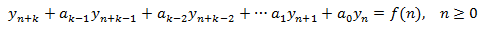
Supongamos que tenemos una solución de la EDFH
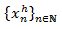
y una solución particular
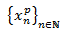
es fácil demostrar que
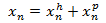
también es solución.
La solución general de la EDF es
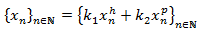
Pero encontrar una solución particular no es una tarea sencilla, nos puede ayudar la siguiente tabla:
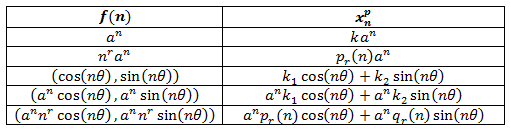
Podemos encontrar EDF resueltas en este enlace.

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.

