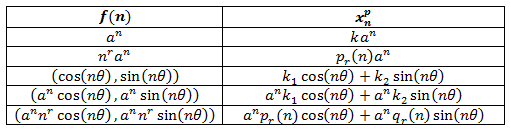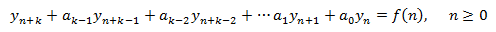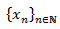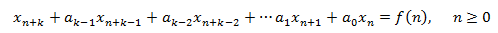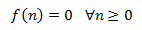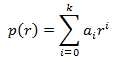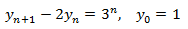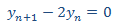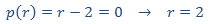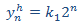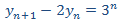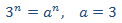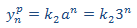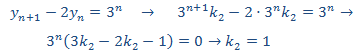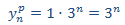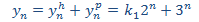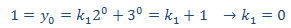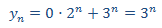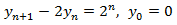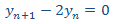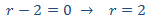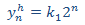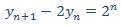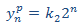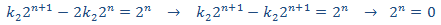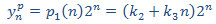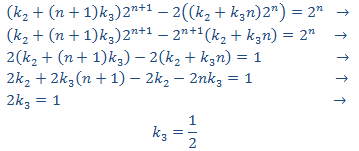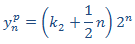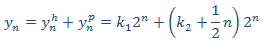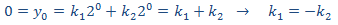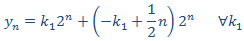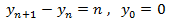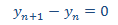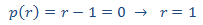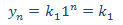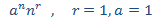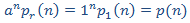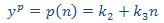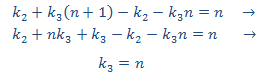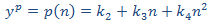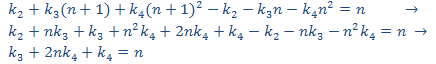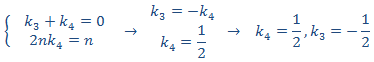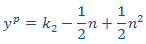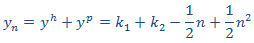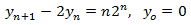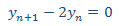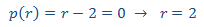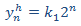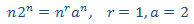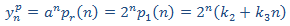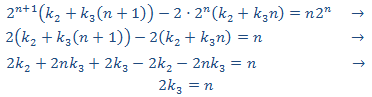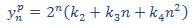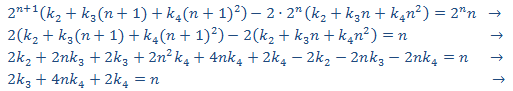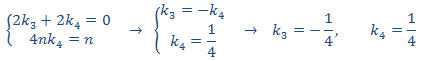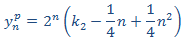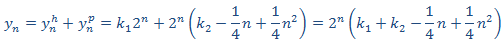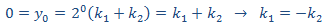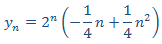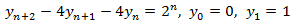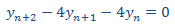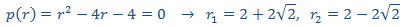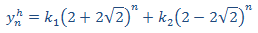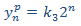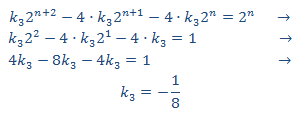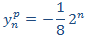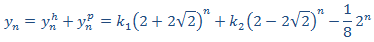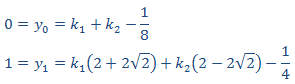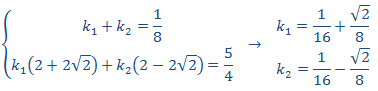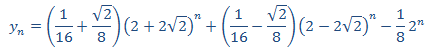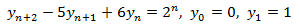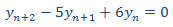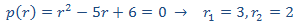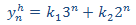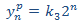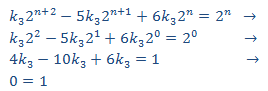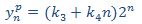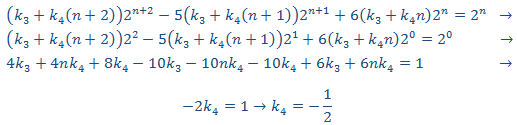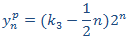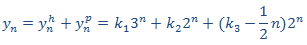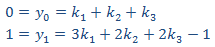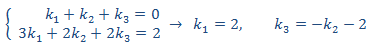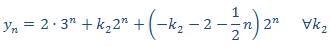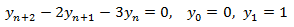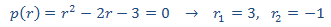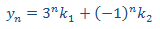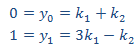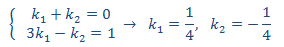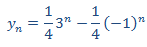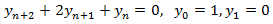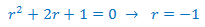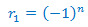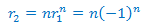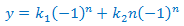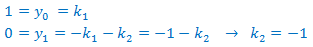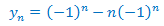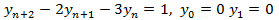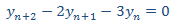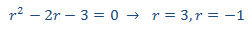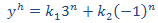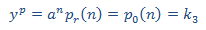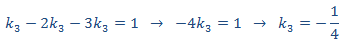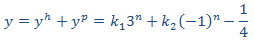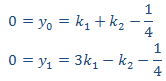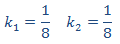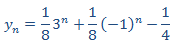Ecuaciones en Diferencias Finitas Resueltas
|
|
Contenido de esta página:
-
Introducción
-
Tabla de Soluciones Particulares
-
Recordemos que... Definición de EDF, EDFH, Solución y Polinomio Característico
-
Resolución de EDF's de primer y segundo orden
Enlace: Teoría sobre EDF's
Introducción
En esta sección resolveremos ecuaciones en diferencias finitas (EDF) de primer y segundo orden no homogéneas.
Al igual que en otros tipos de ecuaciones, como las ecuaciones diferenciales, la solución de una EDF no homogénea es la suma de la solución de la homogénea y de una solución particular:
x = xh + xp
Tanto en las de primer y segundo orden, para obtener la solución de la homogénea calcularemos el polinomio característico de la EDF. En el caso de las de segundo orden, éste será un polinomio
de segundo orden, con lo que tendremos dos soluciones y habrá que distinguir los casos en que son reales distintas, real de multiplicidad doble o complejas.
Obviaremos el método o algoritmo para resolver las EDFs, que es extenso y podemos encontrar aquí, y sólo mostramos una tabla con las soluciones particulares típicas (la primera columna es el término independiente y la segunda la solución particular).
Soluciones Particulares
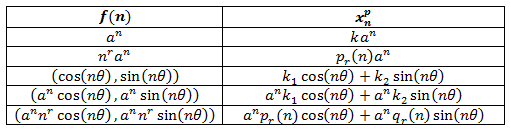
Recordemos que...
Una EDF (ecuación en diferencias finitas) de orden k es
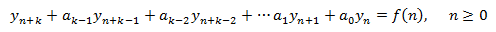
y diremos que una sucesión
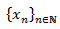
es solución si verifica la EDF, esto es, si
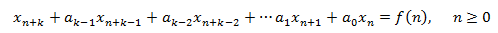
Diremos que la EDF es homogenia (EDFH) si
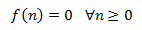
Definimos el polinomio característico de una EDF como
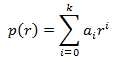
Finalmente, comentamos que una de las aplicaciones de las EDF es el estudio de la evolución de las
variables temporales en Economía cuando se considera al tiempo como una variable discreta.
Podemos encontrar más información sobre su utilidad y orígenes en el siguiente artículo de
la Revista de métodos cuantitativos para la Economía y la Empresa que podemos
encontrar en este enlace.
EDF's Resueltas
| Ejercicios resueltos (click para ver solución) |
| 1 |
|
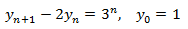
|
| SOLUCIÓN |
|
Primero resolvemos la EDFH
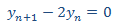
que tiene el polinomio característico
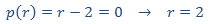
Tenemos la solución
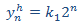
Ahora resolvemos la EDF completa:
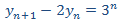
Buscamos una solución particular teniendo en cuenta el término independiente:
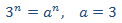
Planteamos la solución particular
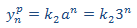
Sustituimos en la EDF
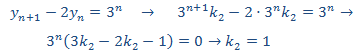
Por tanto, tenemos la solución
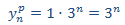
La solución general de la EDF es la suma de la solución de la EDFH i la particular de la completa, es decir,
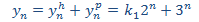
Finalmente, con la condición de valor inicial obtenemos la constante que nos queda:
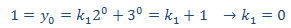
Por tanto, la solución es
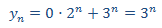
|
|
|
| 2 |
|
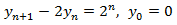
|
| SOLUCIÓN |
|
Primero resolvemos la EDFH
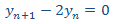
que tiene el polinomio característico
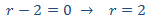
Por tanto, la solución de la homogenia es
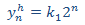
Ahora buscamos una solución particular de la EDF completa:
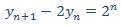
Por la forma del término independiente, planteamos la solución
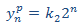
Sustituimos en la EDF
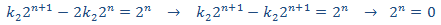
Puesto que no es viable, planteamos la solución
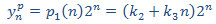
Sustituimos en la EDF
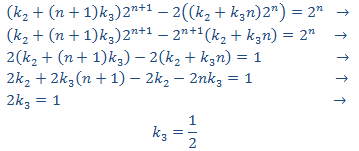
Tenemos la solución particular
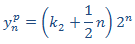
La solución general es
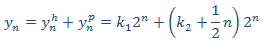
Aplicamos la condición inicial:
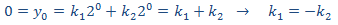
Por tanto, la solución es
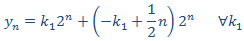
|
|
|
| 3 |
|
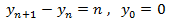
|
| SOLUCIÓN |
|
Resolvemos la EDFH
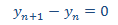
que tiene el polinomio característico
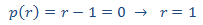
y nos proporciona la solución
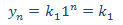
Ahora resolvemos la EDF completa. Por el término independiente,
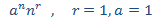
planteamos la solución particular
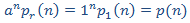
donde p(n) es un polinomio de grado 1, es decir,
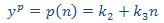
Sustituimos en la EDF
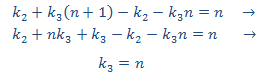
Puesto que esto no es viable, utilizamos un polinomio de grado 2
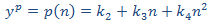
Sustituimos en la EDF
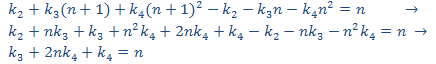
Igualando coeficientes
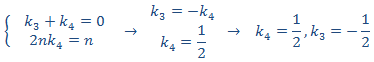
No hay condiciones sobre k2.
Aplicamos la condición inicial
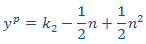
Por tanto, la solución de la EDF es
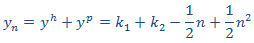
|
|
|
| 4 |
|
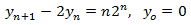
|
| SOLUCIÓN |
|
Resolvemos la EDFH
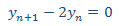
que tiene el polinomio característico
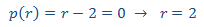
y nos proporciona la solución de a EDFH
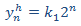
Ahora resolvemos la completa. Teniendo en cuenta la forma del término independiente
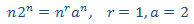
Planteamos la solución particular
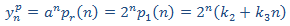
Sustituimos en la EDF
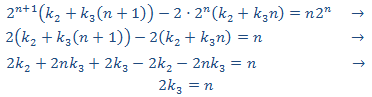
Esto no es viable. Puesto que en la solución de la homogenia tenemos un monomio de grado 0, probamos con uno de segundo grado:
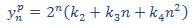
Sustituimos en la EDF
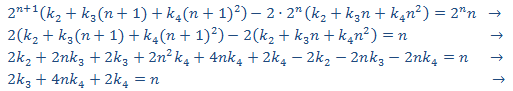
Igualando coeficientes, obtenemos el sistema
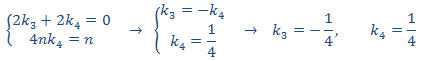
con lo que la solución particular es
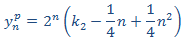
Por tanto, la solución general es
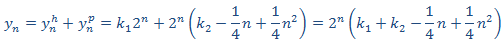
Aplicamos la condición inicial
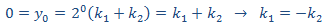
Y tenemos la solución
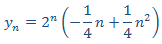
|
|
|
| Ejercicios resueltos (click para ver solución) |
| 5 |
|
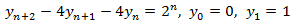
|
| SOLUCIÓN |
|
Resolvemos la EDFH
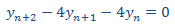
que tiene el polinomio característico
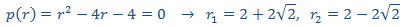
Al ser raíces simples y reales sabemos que la solución de la homogenia es
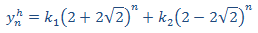
Ahora resolvemos la EDF completa. Teniendo en cuenta la forma del término independiente, planteamos la solución particular
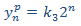
Sustituimos en la EDF
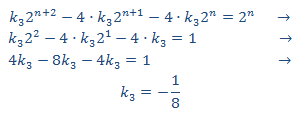
Por tanto, tenemos la solución particular
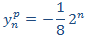
Con lo que tenemos la solución general
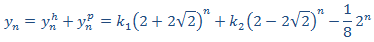
Aplicamos la condición inicial:
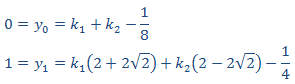
y obtenemos el sistema
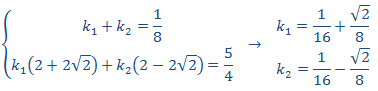
Finalmente, la solución de la EDF es
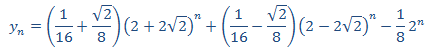
|
|
|
| 6 |
|
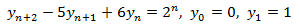
|
| SOLUCIÓN |
|
Resolvemos la EDFH
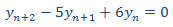
con polinomio característico
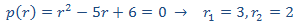
puesto que las raíces son reales y simples, sabemos que la solución de la EDFH
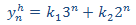
Ahora resolvemos la EDF completa. Por la forma del término independiente, planteamos la solución
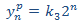
Sustituimos en la EDF
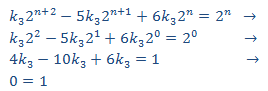
Puesto que esto no es viable, proponemos la solución
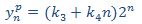
Sustituimos en la EDF
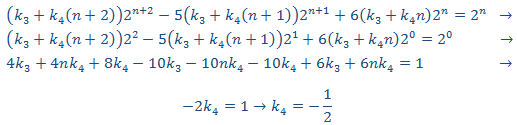
Por tanto, tenemos la solución particular
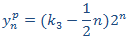
y, la solución general
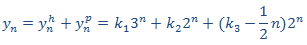
Aplicamos la condición inicial
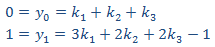
obteniendo el sistema
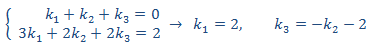
Finalmente, la solución de la EDF es
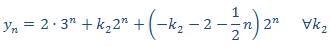
|
|
|
| 7 |
|
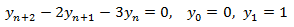
|
| SOLUCIÓN |
|
El polinomio característico de la EDF (que es homogenia) es
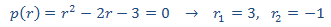
Puesto que las raíces son reales y simples, la solución es
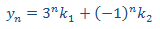
Aplicamos la condición inicial
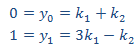
Obteniendo el sistema
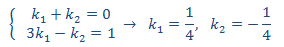
Con lo que la solución de la EDF es
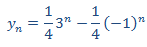
|
|
|
| 8 |
|
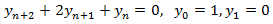
|
| SOLUCIÓN |
|
El polinomio característico es
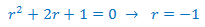
Como solo hay una raíz real y doble, sabemos que una solución es
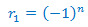
y que también lo es
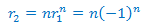
Por tanto, tenemos la solución general
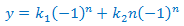
Aplicamos la condición inicial
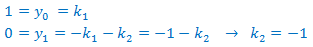
Con lo que la solución es
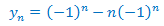
|
|
|
| 9 |
|
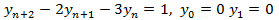
|
| SOLUCIÓN |
|
Resolvemos la EDFH
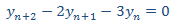
con polinomio característico
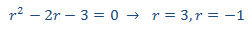
como las raíces son reales y simples, sabemos que la solución general de la homogenia es
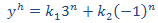
Ahora buscamos una solución particular de la no homogenia.
Por la forma del término independiente,
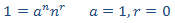
proponemos la solución particular
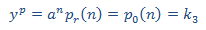
Sustituimos en la EDF
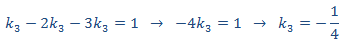
Por tanto, tenemos la solución general
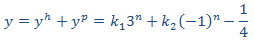
Aplicamos las condiciones iniciales
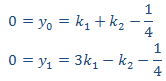
La solución del sistema es
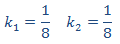
Finalmente, la solución de la EDF es
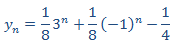
|
|
|


Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.