Contenido de esta página:
-
Introducción.
-
Definición de Máquina de Turing (de una cinta).
-
Lenguaje de una Máquina de Turing.
-
Ejemplos de Máquinas de Turing.
-
Algunos Teoremas sobre las Máquinas de Turing y su lenguaje.
Páginas relacionadas:
Introducción
La máquina de Turing, presentada por Alan Turing en 1936 en
On computable numbers, with an application to the Entscheidungsproblems, es el modelo matemático de un dispositivo que se comporta como un autómata finito y que dispone de una cinta de longitud infinita en la que se pueden leer, escribir o borrar símbolos. Existen otras versiones con varias cintas, deterministas o no, etc., pero todas son equivalentes (respecto a los lenguajes que aceptan).
Uno de los teoremas más importantes sobre las máquinas de Turing es que pueden simular el comportamiento de una computadora (almacenamiento y unidad de control). Por ello, si un problema no puede ser resuelto por una de estas máquinas, entonces tampoco puede ser resuelto por una computadora
(problema indecidible, NP).
La notación de las máquinas de Turing es sencilla y exacta, por lo que es más cómodo trabajar con ellas a la hora de estudiar qué problemas son
decidibles (P) y cuáles indecidibles
(NP).
Por el momento la relación de inclusión entre P y NP
está por demostrar, aunque sí sabemos que
$$ P \subseteq NP $$
Además, diremos que los lenguajes aceptados por los
Autómatas Finitos (Deterministas o no, con o sin transiciones-ε, con o sin pila...)
pueden ser aceptados también por alguna máquina de Turing.
En esta página veremos la definición de la Máquina de Turing, algunos ejemplos, su lenguaje y algunos
teoremas que la relacionan con los Autómatas Finitos.
Definición de la Máquina de Turing
Llamamos Máquina de Turing (ó MT) a
$$ M =(Q, \Sigma, \mathcal{T}, \delta, q_0, B, F) $$
donde
Q es el conjunto finito de estados que denotaremos
por
$$ q_0, q_1, q_2,... $$
Σ es el alfabeto: el conjunto finito de
símbolos de entrada.
Τ es el conjunto de símbolos de cinta. El alfabeto es
un subconjunto de Τ.
q0 es el estado inicial: el estado en el
que se encuentra inicialmente la MT.
B es un elemento de Σ: el símbolo en blanco.
Se encuentra en todas las casillas de la cinta que no tienen
un símbolo de entrada.
F es el conjunto de estados finales.
δ es la función de transiciones.
La expresión
$$ \delta(q, X) = (p, Y, D) $$
indica que en el estado q, si la cabeza de la MT señala al símbolo
de cinta X, entonces la MT escribe el símbolo de cinta Y en la
casilla actual (cambia X por Y ) y mueve la cabeza una casilla
hacia D
(D puede ser derecha, R; o izquierda, L) y pasa al estado
p.
La cinta de la MT está formada por infinitas casillas.
Inicialmente, la palabra de entrada (una concatenación de símbolos del alfabeto) se
encuentra escrita en casillas consecutivas de la cinta y la cabeza señala al primer símbolo
de la palabra. Todas las otras casillas (hacia la izquierda y la derecha) contienen el símbolo en blanco.
Lenguaje de una Máquina de Turing
El lenguaje de una Máquina de Turing
$$ M =(Q, \Sigma, \mathcal{T}, \delta, q_0, B, F) $$
es
$$ L(M):= \{ w\in {\Sigma }^* \ : \ q_0 w \vdash ^* \ \alpha p \beta, p\in F, \alpha, \beta \in \mathcal{T} ^* \}$$
Es decir, las w de Σ* tales que la máquina de Turing alcanza un
estado de aceptación.
Lenguaje Recursivo
Sea L el lenguaje de una máquina de Turing M, es decir,
L = L(M), y además,
si w es una palabra de L, entonces M se para (y alcanza
un estado de aceptación)
si w no es una palabra de L, entonces M se para (pero
no alcanza un estado de aceptación)
entonces se dice que L es un lenguaje recursivo.
Problema 1
Máquina de Turing que proporciona el complemento a 1 de un número binario.
Ver solución
La MT tendrá escrita en la cinta un número de n cifras (bits) en binario
(ceros y unos). Tiene que cambiar los 0's por 1's y viceversa.
Inicialmente, la cabeza de la MT señala la primera cifra del número (la que
está más a la izquierda). Las otras casillas tienen el símbolo en blanco.
La cinta de la MT es

La MT tendrá únicamente dos estados: el inicial, q0, y el
de aceptación o final, q1.
La MT se mantiene en el estado q0 mientras realiza
la conversión. Cuando haya finalizado, pasa al estado q1.
Función de Transiciones:
$$ \delta(q_0, 1) = (q_0, 0, R) $$
Es decir, si la cabeza señala un 1, lo cambia por un 0 y se mueve hacia
la derecha.
$$ \delta(q_0, 0) = (q_0, 1, R) $$
Es decir, si la cabeza señala un 0, lo cambia por un 1 y se mueve hacia
la derecha.
$$ \delta(q_0, B) = (q_1, B, R) $$
Es decir, cuando la cabeza señala el primer símbolo en blanco, la cabeza
se mueve a la derecha y la MT pasa al estado final.
Por tanto, la MT es
$$ M =(\{ q_0,q_1 \} ,\{ 0,1\} ,\{ 0,1,B\} , \delta,q_0,B,\{ q_1 \} ) $$
siendo δ la función de transición definida por:
$$\delta (q_0,0)=(q_0,1,R) $$
$$\delta (q_0,1)=(q_0,0,R) $$
$$\delta (q_0,B)=(q_1,B,R) $$
Notemos que la MT se para al llegar al estado de aceptación
q1 ya que para este estado no tenemos definida la función
de transición.
Problema 2
Diseñar una máquina de Turing que calcula el número consecutivo de un número dado en
binario.
Ver solución
Si el número es par, su último bit es 0. La máquina sólo tiene que
cambiar este 0 por un 1.
Si el número es impar, su último bit es 1. En este caso,
se tiene que cambiar por 0’s todos los 1’s seguidos que haya escritos
de derecha a izquierda hasta llegar al primer 0, que se cambia por un 1.
Si no hay ningún 0, entonces se tiene que añadir un 1 delante del número
(añadir un bit). Es decir, escribir un 1 en la casilla en blanco (B)
a la izquierda del número.
Vamos a considerar tres estados:
$$ q_0, q_1, q_2$$
Inicialmente, la MT está en el estado q0 con
la cabeza señalando la primera cifra del número.
La MT recorre todo el número para ver si es par o impar sin modificar su cinta.
$$ \delta (q_0, 0) = (q_0, 0, R) $$
$$ \delta (q_0, 1) = (q_0, 1, R) $$
Notemos que, por ahora, la MT se detiene al llegar al primer símbolo en
blanco a la derecha del número.
La MT vuelve a la anterior casilla (último número). Si es un 0, lo cambia por un 1
y pasa al estado final que es q2 . Para hacer esto usaremos
el estado q1 :
$$ \delta (q_0, B) = (q_1, B, L)$$
$$ \delta (q_1, 0) = (q_2, 1, R)$$
-
Si el número es impar, la MT no ha cambiado el último número, pero está
en el estado q1 . Tiene que cambiar todos los 1's consecutivos
que haya de derecha a izquierda.
$$ \delta (q_1, 1) = (q_1, 0, L) $$
Por ahora, la MT se para cuando llega al primer 0 (de derecha a izquierda)
ó en un símbolo en blanco. Si es un 0, lo cambia por un 1 y el proceso finaliza:
$$ \delta (q_1, 0) = (q_2, 1, L) $$
(Hemos escrito un desplazamiento a la izquierda, pero esto no tiene importancia ya que
la MT ha llegado al estado final).
Si lo que señala la cabeza es un blanco en vez de un 1, tiene que cambiarlo
por un 1 y finalizar el proceso.
$$ \delta(q_1, B) = (q_2, 1, L) $$
El diagrama de la máquina es
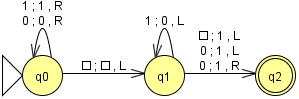
Donde el cuadro representa el símbolo en blanco B.
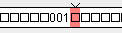
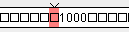
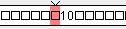
Vamos a simular la MT para varias entradas. Mostraremos el estado final de la cinta
y la posición de la cabeza (sombreado en color rosa).
Entrada: 000; Resultado esperado: 001.
Entrada: 0011; Resultado esperado: 0100.

Entrada: 111; Resultado esperado: 1000.
Entrada: 1; Resultado esperado: 10.
Problema 3
Diseñar una máquina de Turing que acepta el lenguaje
$$ L=\{ 0^n 1^n \ : n>0 \} $$
Ver solución
Lo primero que haremos es limitar el alfabeto a
$$ \Sigma = \{0, 1\} $$
así nos aseguramos de que sólo puede aceptar palabras con
de entrada con símbolos 1 y 0.
Los símbolos de cinta serán
$$ \mathcal{T} = \{0, 1, B, X, Y \} $$
siendo B el símbolo en blanco.
La MT consta de cinco estados:
$$ q_0, q_1, q_2, q_3, q_4 $$
Los estados q0 y q4 son el inicial
y el final, respectivamente.
Inicialmente, la cabeza señala el primer 0. Lo cambia por X y se desplaza a la derecha en busca del
primer 1 para cambiarlo por Y:
$$ \delta(q_0, 0) = (q_1, X, R) $$
$$ \delta(q_1, 0) = (q_1, 0, R) $$
Es decir, mientras haya 0's, se mantiene en el estado q1 .
$$ \delta (q_1, 1) = (q_2, Y, L) $$
Ha encontrado el primer 1. Lo cambia por Y y pasa al estado q2
moviéndose a la izquierda. En este estado, la MT se mueve hacia la izquierda en busca de X saltando las casillas con 0's:
$$ \delta (q_2, 0) = (q_2, 0, L) $$
Cuando encuentra la X, se mueve hacia la derecha esperando encontrar un 0 para cambiarlo por
X, por lo que pasa al estado q0 :
$$ \delta (q_2, X) = (q_0, X, R) $$
Una vez cambiado dicho 0 por X, está en el estado q1 . Ahora tiene
que buscar el siguiente 1 y cambiarlo por Y, pero se encuentra con Y antes de llegar,
por lo que tiene que saltar esta casilla:
$$ \delta (q_1, Y) = (q_3, Y, R) $$
En el estado q3 sigue saltando las casillas con Y hasta llegar
al 1:
$$ \delta (q_3, Y) = (q_3, Y, R) $$
$$ \delta (q_3, 1) = (q_2, Y, L) $$
Pasa al estado q2 una vez ha cambiado el 1 por la Y. En este
estado, la MT se mueve a la izquierda hasta encontrar una X. Una vez la encuentra, se mueve una casilla a
la derecha. Si hay un 0, tendrá que empezar el proceso anterior (buscar 1, cambiarlo por Y y volver a buscar
la X, con lo que estaremos de nuevo en este punto). Si ya no quedan 0's, habrá una
Y y, por tanto, se han cambiado n 0's por n X 's y
n 1's por n Y 's. Entonces se mueve a la izquierda:
$$ \delta(q_2, Y) = (q_2, Y, L) $$
Se encuentra con una X y pasa al estado q0. En este estado
se busca un 0 para cambiarlo por X, pero suponemos que ya no quedan. Entonces la cabeza debe moverse
a la derecha para comprobar que tampoco quedan más 1's:
$$ \delta(q_0, Y) = (q_0, Y, R) $$
Cuando encuentra el primer símbolo en blanco, la MT finaliza:
$$ \delta(q_0, B) = (q_4, B, R) $$
En el caso de que haya más 0's que 1's, llegará un momento en el
que ya no queden 1's (los habrá cambiado por
Y ). La MT se
quedará permanentemente en el estado
q1 .
El diagrama de la MT es
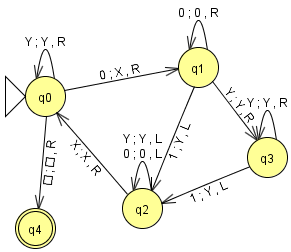
Vamos a simular la MT para una sola entrada que todas tienen la misma forma. Mostraremos el estado final de la cinta
y la posición de la cabeza (sombreado en color rosa).
Entrada: 000111; Resultado esperado: XXXYYY.

Problema 4
Diseñar una Máquina de Turing que, dada una palabra w del alfabeto Σ={0, 1}, proporciona su
reverso, wR .
Ver solución
Lo que tiene que hacer la MT es cambiar el orden de
los símbolos que hay en su cinta.
Usaremos los símbolos de cinta adicionales A y Z para indicar
el comienzo y el final de la palabra w en la cinta.
En el estado q0 , la MT busca el comienzo de palabra, es decir,
el primer símbolo en blanco a la izquierda. Cuando lo encuentra, lo cambia por A:
$$ \delta(q_0, 0) = (q_0, 0, L) $$
$$ \delta(q_0, 1) = (q_0, 1, L) $$
En el estado q1 la MT se desplaza hacia la derecha hasta encontrar
el primer símbolo en blanco para cambiarlo por Z:
$$ \delta(q_1, 0) = (q_1, 0, R) $$
$$ \delta(q_1, 1) = (q_1, 1, R) $$
$$ \delta(q_1, B) = (q_2, Z, L) $$
Luego pasa al estado q2 . En este estado, cambia el primer
elemento de la palabra w (o sea, el último) por B para escribirlo al
lado derecho de Z.
Como usaremos este estado posteriormente, puede ocurrir que ya no queden símbolos de
w porque ya se ha copiado. En este caso sólo quedarán símbolos en blanco y
el símbolo A que marca el comienzo de w:
$$ \delta(q_2, B) = (q_2, B, L) $$
$$ \delta(q_2, A) = (q_8, B, L) $$
$$ \delta(q_2, 1) = (q_3, B, R) $$
$$ \delta(q_2, 0) = (q_6, B, R) $$
En el caso de que ya no haya símbolos de w, la MT borra A
y vuelve pasa al estado q8 en el que buscará la Z para
borrarla de la cinta, pasando al estado final q9 :
$$ \delta(q_8, B) = (q_8, B, R) $$
$$ \delta(q_8, Z) = (q_9, B, R) $$
Volviendo al punto anterior, si en q2 se encuentra con el
símbolo 1, entonces lo borra y entra en los estados q3 y
q4 cuya finalidad son escribir el 1 en su sitio correspondiente
a la derecha de Z:
$$ \delta(q_3, B) = (q_3, B, R) $$
$$ \delta(q_3, Z) = (q_4, Z, R) $$
$$ \delta(q_4, B) = (q_5, 1, R) $$
$$ \delta(q_4, 0) = (q_4, 0, R) $$
$$ \delta(q_4, 1) = (q_4, 1, R) $$
En el estado q5 la MT busca de nuevo el símbolo Z
para pasar de nuevo al estado q2 :
$$ \delta(q_5, 0) = (q_5, 0, L) $$
$$ \delta(q_5, 1) = (q_5, 1, L) $$
$$ \delta(q_5, Z) = (q_2, Z, L) $$
El otro caso es que en q2 se encuentre con el símbolo 0.
La MT procede de forma análoga a los estados q3 y
q4 pero escribiendo 0 en vez de 1. Para ello usaremos
los estados q6 y
q7:
$$ \delta(q_6, B) = (q_6, B, R) $$
$$ \delta(q_6, Z) = (q_7, Z, R) $$
$$ \delta(q_7, B) = (q_5, 0, L) $$
$$ \delta(q_7, 0) = (q_7, 0, R) $$
$$ \delta(q_7, 1) = (q_7, 1, R) $$
Finalmente, en la cinta sólo quedará la palabra wR, es decir,
la palabra w escrita de derecha a izquierda.
El diagrama de la máquina de Turing es
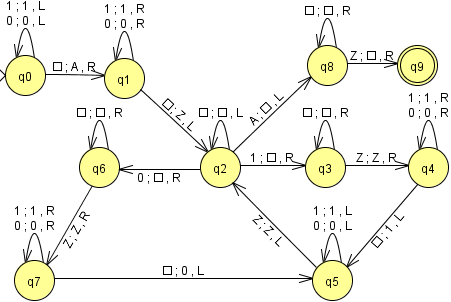
Teoremas sobre las máquinas de Turing
Lenguaje Recursivamente Enumerable
Recordemos que llamamos lenguaje Recursivamente Enumerable (RE) a los
lenguajes que pueden ser aceptados por una Máquina de Turing.
Teorema 1
Todo lenguaje aceptado por una Máquina de Turing de varias
cintas es Recursivamente Enumerable.
Teorema 2
Sea L = L(M) el lenguaje que acepta una máquina de Turing no determinista M,
entonces existe una máquina de Turing deterministaN que acepta dicho lenguaje, es
decir, L(M) =L (N).
Lenguajes de máquinas de Turing y de Autómatas
Teorema 3
Sea L el lenguaje aceptado por una máquina de Turing, entonces existe
algún Autómata de dos pilas que acepta L.
Teorema 4
Todo lenguaje Recursivamente Enumerable es aceptado por alguna máquina de
tres contadores.
Teorema 5
Todo lenguaje Recursivamente Enumerable es aceptado por alguna máquina de
dos contadores.
Inicio

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.










