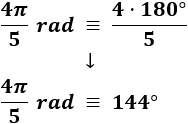Calculadora: conversión entre grados y radianes
Contenido de esta página:
- 3 calculadoras online para pasar de grados a radianes y viceversa
- Equivalencia entre grados y radianes
- Regla de tres para cambiar entre las unidades
- 6 problemas resueltos
Otras calculadoras: indice de calculadoras.
Calculadoras de conversión
Las calculadoras aplican una regla de tres directa, teniendo en cuenta que 180 grados son \(\pi\) radianes.
Nota: se admiten números decimales utilizando un punto (como 3.14) y fracciones utilizando una barra (como 5/4).
Tenemos tres calculadoras:
1. Pasar de grados a radianes:
| Grados | Radianes |
|---|---|
| \( 180^\circ\) | \(\pi \ rad\) |
| \(^\circ\) | \( x \) |
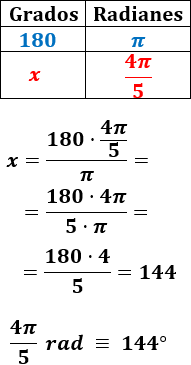
2. Pasar de radianes (con \(\pi\)) a grados:
| Grados | Radianes |
|---|---|
| \( 180^\circ\) | \(\pi \ rad\) |
| \( x \) | \(·\pi \ rad\) |
3. Pasar de radianes (sin \(\pi\)) a grados:
| Grados | Radianes |
|---|---|
| \( 180^\circ\) | \(\pi \ rad\) |
| \( x \) | \( \ rad\) |
Equivalencia entre grados y radianes
Tanto los grados como los radianes son unidades de medida de ángulos, así que tenemos que saber pasar de una unidad a otra.
Símbolos de las unidades
- Grados: el símbolo de los grados es "°". Por ejemplo, 90 grados se escriben como \(90^\circ\).
- Radianes: el símbolo de los radianes es la abreviatura "rad". Por ejemplo, 3 radianes son \(3\ rad\).
Nota: en los radianes veremos casi siempre el número pi, \(\pi\), y tenemos que acostumbrarnos a ello. Esto se debe a que es un número irracional y, por tanto, si lo aproximamos, estamos perdiendo precisión.
Relación grados-radianes
Un ángulo de 360 grados (es decir, el ángulo de una circunferencia completa) equivale a \(2·\pi\) radianes:
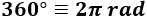
Como dato curioso, el radián se define como la razón entre la longitud de arco y su radio \(R\). Teniendo en cuenta que la longitud de una circunferencia completa es \(2\pi R\), su ángulo en radianes es
$$ \alpha = \frac{2·\pi·R}{R} = 2\pi\ rad $$
La relación entre ángulos y radianes es una relación de proporcionalidad directa, lo que implica que podemos pasar de una unidad de medida a la otra mediante una regla de tres directa.
Por ejemplo, dividiendo entre 2, tenemos
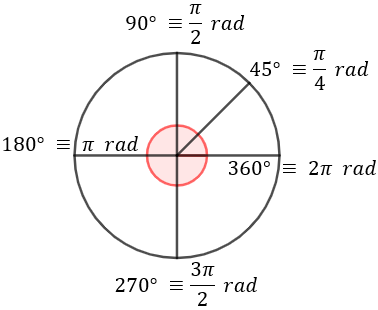
- \(180^\circ\) son \(\pi \ rad \)
- \(90^\circ\) son \(\frac{\pi }{2}\ rad\)
- \(45^\circ\) son \(\frac{\pi }{4} \ rad \)
Regla de tres: ejemplos de cambio
Como dijimos, para pasar de radianes a grados o viceversa, utilizamos una regla de tres directa. A la hora de aplicar la regla, solemos utilizar la equivalencia 360º ≡ 2\(\pi\) rad, o bien, 180º≡ \(\pi\) rad.
Ejemplo 1 (de grados a radianes): pasamos 135 grados a radianes.
Ejemplo 2 (de radianes a grados): pasamos \(4\pi /5\ rad\) a grados:
Problemas Resueltos
Problema 1 
Escribir en grados los ángulos representados:
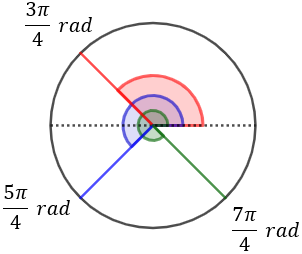
Para pasar de radianes a grados es suficiente con cambiar el número \(\pi\) por 180°:
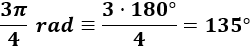
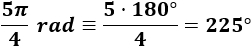
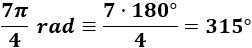
Problema 2 
Pasar a radianes los siguientes ángulos dados en grados: 60°, 100°, 150°, 200°, 250° y 300°.
Aplicaremos una regla de tres teniendo en cuenta que 180° son \(\pi\) rad:
Pasamos 60° a radianes:
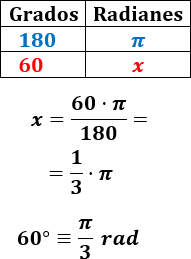
Pasamos 100° a radianes:
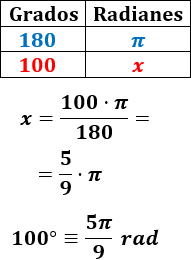
Pasamos 150° a radianes:

Pasamos 200° a radianes:
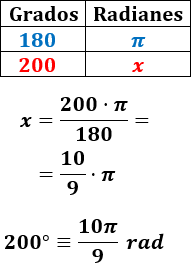
Pasamos 250° a radianes:
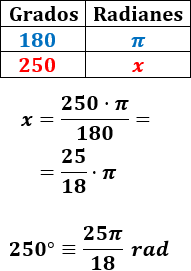
Pasamos 300° a radianes:

Problema 3 
Pasar a grados los siguientes ángulos escritos en radianes: \(\pi /5\), \(3\pi /5\), \(2\pi /3\), y \(5\pi /2\).
Pasamos \(\pi /5 \ rad\) a grados:
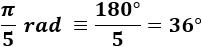
Pasamos \(3\pi /5 \ rad\) a grados:
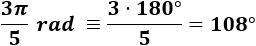
Pasamos \(2\pi /3 \ rad\) a grados:
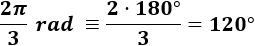
Pasamos \(5\pi /2 \ rad\) a grados:
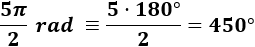
Problema 4 
¿Cuántas vueltas completas son \(3\pi\) radianes? ¿Y 450 grados?
Una vuelta completa es un ángulo de \(2\pi\) radianes. Entonces, media vuelta es uno de \(\pi\) radianes. Por tanto, \(3\pi\) radianes es una vuelta completa y media (porque \(3\pi = 2\pi + \pi\). .
En grados, una vuelta completa es un ángulo de 360 grados y un ángulo de 90 grados es un cuarto de vuelta. Por tanto, 450 grados es una vuelta completa y un cuarto.
Problema 5 
Representar en una circunferencia:
- Un ángulo de \(-\pi \ rad\).
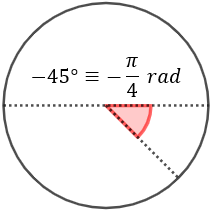
- Un ángulo de \(-45^\circ\).
Si el ángulo es negativo, representamos el ángulo en sentido contrario.
- Representación de un ángulo de \(-\pi \ rad\):
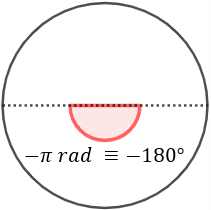
- Representación de un ángulo de \(-45^\circ\):
Problema 6 
Calcular (y representar) las dos siguientes sumas de ángulos:
- Suma de un ángulo de 90 grados con uno de 45.
- Suma de un ángulo de \(\pi /3\) radianes con uno de \( \pi/2\).
- Suma de un ángulo de 90 grados con uno de 45:
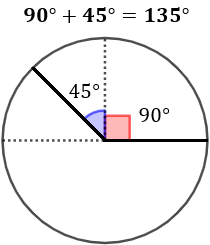
- Suma de un ángulo de \(\pi /3\) radianes con uno de \( \pi/2\):
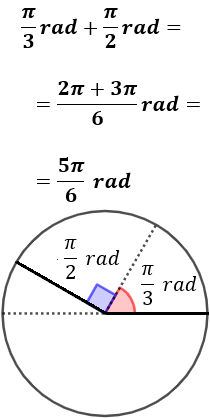
Calculadora: cambio entre grados y radianes - (c) - matesfacil.com

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.