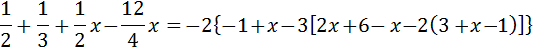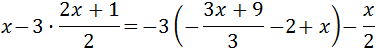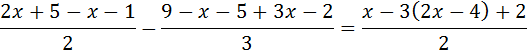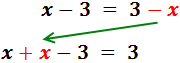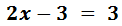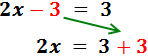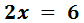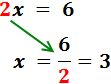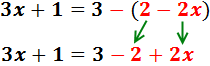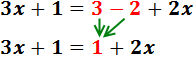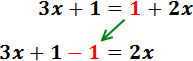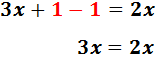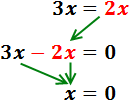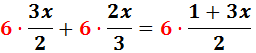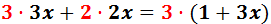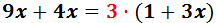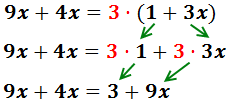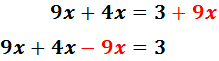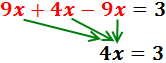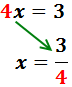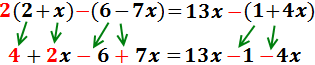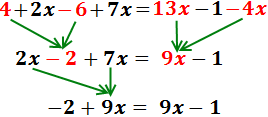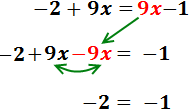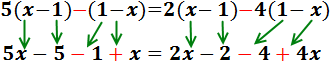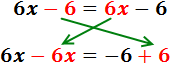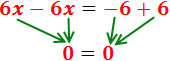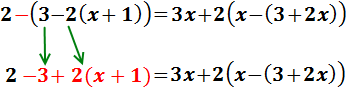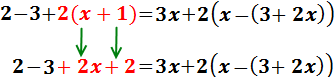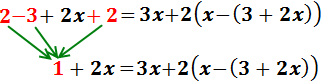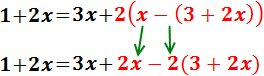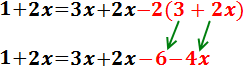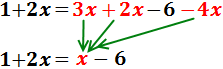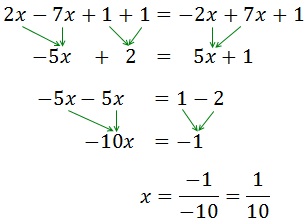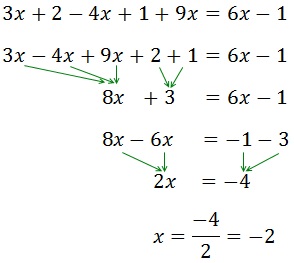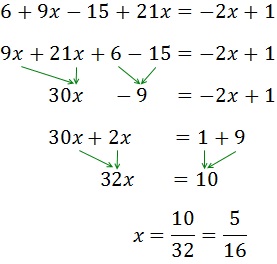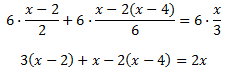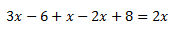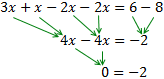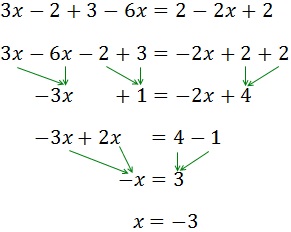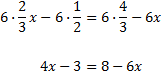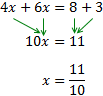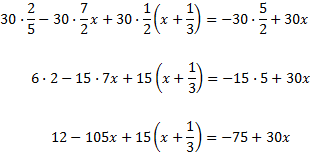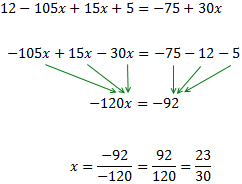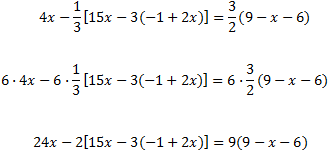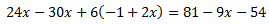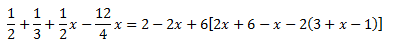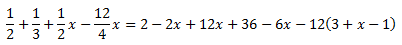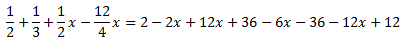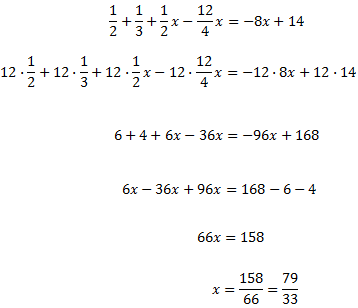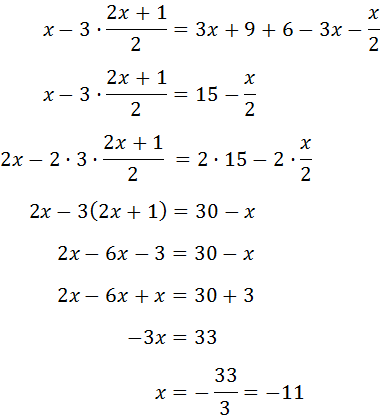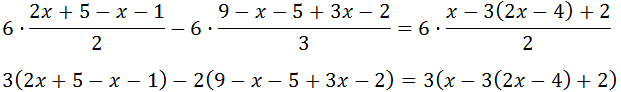EQUACIONS DE PRIMER GRAU RESOLTES
|
Contingut d'aquesta pàgina:
Novetat!
Intel·ligència artificial
Com els algorismes condicionen les nostres vides
Enric Senabre, Vicent Costa
Més informació: sembra llibres.
|
 |
Introducció
Pel que fa a les matemàtiques, les equacions de primer grau són la intrudcció a l'Àlgebra. La seva comprensió és imprescindible per poder resoldre altres tipus d'equacions: de segon grau, exponencials, irracionals, etc. i els seus respectius sistemes d'equacions.
Pel que fa a la vida real, encara que no ho semble, les equacions són una eina que ens permeten resoldre els problemes amb què ens topem
diàriament. Podem comprovar-ho en la secció de problemes amb equacions.
Com ja indica el seu nom, en les equacions de primer grau la part literal dels monomis no
tenen exponent major que 1 (per exemple, 3x pot aparèixer a una equació de primer grau però, 3x 2
no perquè és un monomi de segon grau). Precisament aquest fet ens assegura que, en cas d'existir solució,
només n'hi ha una (excepte el cas especial en què n'hi ha infinites).
Diem "en cas d'existir solució" ja que algunes equacions no en tenen. Per exemple, l'equació x = x + 1 es pot interpretar como "x és un nombre igual al seu consecutiu". Com que açò mai no pot ser, l'equació no té solució, és a dir, no hi ha cap nombre que sigui igual al seu consecutiu. En aquest exemple, l'equació és equivalent a l'equació 1 = 0, la qual cosa és obviament absurd.
Recordem que:
Si arribem a una igualtat impossible, no hi ha solució.
Per exemple, si arribem a 1 = 0 .
-
Si arribem a una igualtat que sempre es compleix, qualsevol valor per a
x és solució, és a dir, la solució és "tots els nombres reals".
Per exemple, si arribem a 0 = 0 .
Quan hi ha denominadors i volem evitar-los, podem multiplicar tota
l'equació pel mínim comú múltiple d'aquests. Així, al simplificar,
desapareixen.
Per eliminar els parèntesis, multipliquem el coeficient de
davant d'aquests per tots els elements que aquests contenen.
En el cas que el coeficient sigui negatiu, canviarem el signe de tots els sumands.
-
Quan tenim parèntesis niats, és a dir, uns parèntesis
dins d'altres, podem eliminar-los des del més exterior al més interior. És a dir,
primer llevem el parèntesi exterior (multiplicant
el seu contingut pel seu coeficient) i, després, llevem els de dins seguint el mateix procediment: des del més exterior fins al més interior.
25 Equacions de Primer Grau Resoltes
En la Part I, les equaciones són més curtes i s'expliquen tots els
passos. Estan ordenadas de menor a major dificultat. En la Part II, les equaciones són una mica més complicades. I en la Part III, es mostren totes les operacions i passos però, no s'expliquen tan
detalladament.
Part I (6 Equacions)
Equació I.1: equació bàsica
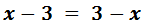
Veure Solució
Passem les x's a un costat de la igualtat
(esquerra) i els nombres a l'altre costat (dreta):
En la dreta, la x està restant. Passa a l'esquerra sumant:
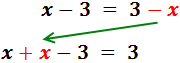
Sumem els monomis amb x’s:
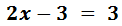
En l'esquerra, el -3 està restant. Passa a la dreta sumant:
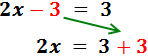
Sumem els monomis de la dreta:
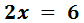
El coeficient de la x és 2. Aquest nombre està multiplicant a x, així
que passa a l'altre costat dividint:
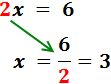
Per tant, la solució de l'equació és x = 3.
Equació I.2: equació amb parèntesi
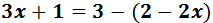
Veure Solució
Recordem que els parèntesis serveixen per agrupar elements,
per simplificar o per evitar ambigüitats.
El signe negatiu de davant del parèntesi indica que els monomis que
conté tenen que canviar de signe:
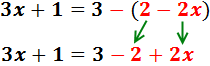
Sumem 3 i -2 en el costat dret:
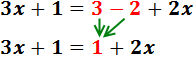
Passem els monomis amb x’s a l'esquerra
i els nombres a la dreta:
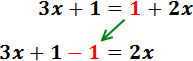
Sumem 1 i -1. Com que el resultat és 0, no l'escrivim:
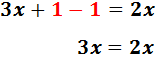
Passem 2x a l'esquerra restant i sumem els monomis:
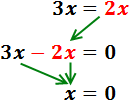
Llavors la solució de l'equació és x = 0.
Equació I.3: equació amb fraccions
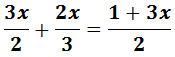
Veure Solució
Tenim diverses maneres de procedir amb les fraccions:
En aquesta equació aplicarem la segona opció.
D'aquesta manera els denominadors van a desaparèixer.
Multipliquem, doncs, pel m.c.m.(2, 3) = 6:
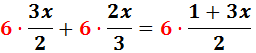
Per simplificar, calculem les divisions:
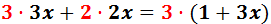
Noteu que hem escrit un parèntesi al eliminar la fracció de la dreta. Açò és perquè el 3 ha de multiplicar tot el numerador i aquest està compost per una suma (un binomi).
Calculem els productes:
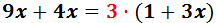
Per eliminar el parèntesi, multipliquem per 3 tots els elements que conté:
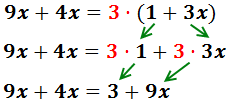
Passem les x’s a l'esquerra:
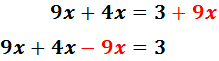
Sumem els monomis:
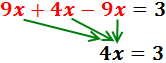
Finalment, el coeficient de la x passa dividint a l'altre costat:
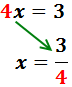
La solució de l'equació és x = 3/4.
La fracció no es pot simplificar més perquè
ja és irreductible (el màxim comú divisor del numerador
i del denominador és 1).
Equació I.4: equació sense solució
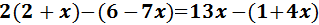
Veure Solució
Eliminem els parèntesis:
El de l'esquerra té un 2 davant, pel que
multipliquem el seu contingut per 2.
Els altres dos parèntesis tenen un signe negatiu davant,
així que canviem els signes dels seus monomis:
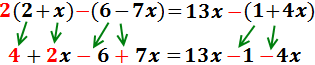
Per simplificar, en cada costat sumem els monomis amb i sense
part literal (els que tenen x i els que no en tenen):
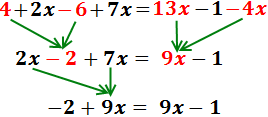
Passem les x’s al costat esquerre i sumem:
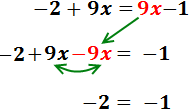
Hem obtingut una igualtat falsa: -2 = -1. Açò significa que l'equació no mai es compleix, sigui quin sigui el
valor de x. Per tant, l'equació no té cap solució.
Equació I.5: equació amb infinites solucions
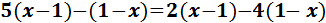
Veure Solució
Eliminem els parèntesis multiplicant els seus respectius
continguts pel nombre que tenen davant.
No s'ha d'oblidar que si el nombre de davant és
negatiu aleshores també s'han de canviar els signes:
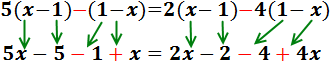
En cada costat, sumem els monomis segons la seva part literal:
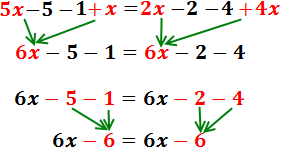
Passem les x’s a l'esquerra i els nombres a la dreta:
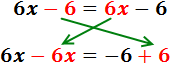
Sumem els monomis:
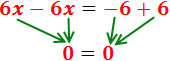
Hem obtingut una igualtat que sempre
es compleix: 0 = 0. Açò significa que l'equació es compleix
sempre, independientement del valor de x.
Per tant, l'equació té infinites solucions
(x pot ser qualsevol nombre i hi ha infinits nombres). Podem expressar-ho com “x és qualsevol real”:
$$ x \in \mathbb{R} $$
Equació I.6: equació amb parèntesis niats
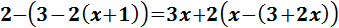
Veure Solució
Primer eliminarem els parèntesis exteriors.
Comencem pel de l'esquerra. Aquest parèntesi
té un signe negatiu davant, pel que canviem el signe als
seus sumands. Un dels sumands és altre parèntesi:
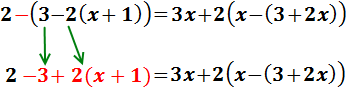
Eliminem el parèntesi que queda en l'esquerra multiplicant per 2:
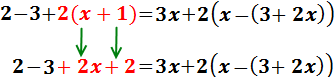
Sumem els nombres en el costat esquerre per simplificar:
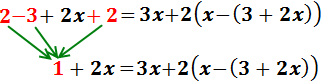
Eliminem el parèntesi exterior de la dreta multiplicant els seus sumands per 2:
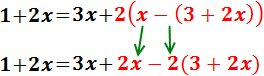
Eliminem el parèntesi que queda multiplicant per 2 i canviant els signes:
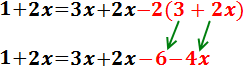
Sumem els monomis en el costat dret:
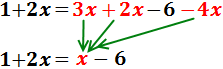
Passem les x’s a l'esquerra, els nombres a la
dreta i simplifiquem:
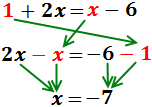
Per tant, la solució és x = -7.
Part II (7 Equacions)
Equació II.1
$$ 3(x+1) -2x = $$
$$ = x-\left( 2 + 3(3 - x)\right) $$
Veure Solució
En aquesta equació tenim parèntesis niats (uns dins d'uns altres).
Anem primer a treure el menut (el de dins). Aquest està multiplicat per
3. Per eliminar-lo, hem de multiplicar per 3 tots els sumands de dins:
$$ 3(x+1) -2x = x-\left( 2 + 3\cdot 3 -3x\right) $$
$$ 3(x+1) -2x = x-\left( 2 + 9 -3x\right) $$
$$ 3(x+1) -2x = x-\left( 11 -3x \right) $$
El interior del parèntesi ja no es pot simplificar més. Com que té un signe negatiu dins,
canviem el signe dels sumands de dins:
$$ 3(x+1) -2x = x - 11 +3x $$
$$ 3(x+1) -2x = - 11 +4x $$
El parèntesi del costat esquerre està multiplicat per 3. Per eliminar-lo, multipliquem tots
els sumands de dins per 3:
$$ 3x +3 -2x = - 11 +4x $$
Ara només hem d'agrupar els monomis segons la seva part literal:
$$ x +3 = - 11 +4x $$
$$ x = -3 - 11 +4x $$
$$ x = -14 +4x $$
$$ x -4x = -14 $$
$$ -3x = -14 $$
Per aïllar la x hem de passar el -3 dividint:
$$ x = \frac{-14}{-3} $$
Com que els signes del numerador i del denominador són negatiu, desapareixen:
$$ x = \frac{14}{3} $$
Ja no podem simplificar més l'expressió de la solució ja que 14 no
és divisible per 3, és a dir, el màxim comú divisor de 14 i 3 és 1.
Equació II.2
$$ 1 - 2 ( 1 + 3x - 2(x + 2) + 3x ) = - 1 $$
Veure Solució
Tenim parèntesis niats (un dins d'un altre) i signes negatius davant d'aquests.
Abans de treballar amb els parèntesi, podem sumar els termes 3x i 3x del parèntesi
exterior ja que es troben en el mateix nivell (no formen part de parèntesi distintos):
$$ 1 - 2 ( 1 + 6x - 2(x + 2)) = - 1 $$
Com que el parèntesi interior està multiplicat per -2, multipliquem per -2 els seus sumands per
poder treure-lo:
$$ 1 - 2 ( 1 + 6x - 2x - 4) = - 1 $$
$$ 1 - 2 ( 6x - 2x - 3) = - 1 $$
$$ 1 - 2 ( 4x - 3) = - 1 $$
Procedim de la mateixa manera que abans:
$$ 1 -8x +6 = - 1 $$
$$ -8x +7 = - 1 $$
$$ -8x = -8 $$
$$ x = \frac{-8}{-8} $$
$$ x = 1 $$
Equació II.3
$$ x + \frac{1}{3} \left(x - 3 -\frac{1}{2}\left(4 - 3x\right)\right)= $$
$$ = \frac{2}{3}\left(1-\frac{5x}{2}\right) $$
Veure Solució
Tenim parèntesis niats multiplicats per fraccions, algunes d'aquestes amb signe negatiu.
Treballarem primer en el costat esquerre de la igualtat. El parèntesi interior està multiplicat
per una fracció negativa. Per eliminar-lo, hem de multiplicar els sumands de dins per
la fracció:
$$ x + \frac{1}{3} \left(x - 3 -\frac{4}{2} +\frac{3x}{2}\right)= $$
$$ = \frac{2}{3}\left(1-\frac{5x}{2}\right) $$
$$ x + \frac{1}{3} \left(x - 3 -2 +\frac{3x}{2}\right)= $$
$$ = \frac{2}{3}\left(1-\frac{5x}{2}\right) $$
$$ x + \frac{1}{3} \left(x -5 +\frac{3x}{2}\right)= $$
$$ = \frac{2}{3}\left(1-\frac{5x}{2}\right) $$
Noteu que si multipliquem per 3 tota l'equació desapareixen dos dels denominadors:
$$ 3x + \frac{3}{3} \left(x -5 +\frac{3x}{2}\right)= 3\frac{2}{3}\left(1-\frac{5x}{2}\right) $$
$$ 3x +\left(x -5 +\frac{3x}{2}\right)= 2\left(1-\frac{5x}{2}\right) $$
El parèntesi de l'esquerra el podem treure (està multiplicat per 1) i el de la dreta el llevem
multiplicant els seus sumands per 2:
$$ 3x + x -5 +\frac{3x}{2}= 2-2\frac{5x}{2} $$
Ara anem agrupant els monomis segons la seva part literal:
$$ 3x + x -5 +\frac{3x}{2}= 2-5x $$
$$ 4x -5 +\frac{3x}{2}= 2-5x $$
$$ 4x +5x +\frac{3x}{2}= 2 + 5 $$
$$ 9x +\frac{3x}{2}= 7 $$
Sumem les fraccions 9x i 3x/2:
$$ \frac{18x}{2} + \frac{3x}{2}= 7 $$
$$ \frac{21x}{2}= 7 $$
$$ x= \frac{7\cdot 2}{21} $$
Escrivim 21 com un producte per reduir la fracció:
$$ x= \frac{7\cdot 2}{7\cdot 3} $$
Els 7's desapareixen i obtenim la solució
$$ x= \frac{2}{ 3} $$
Equació II.4
$$ \frac{x}{2} + \frac{2}{3} = \frac{x}{3} + 1 -\frac{1}{2}\left(1-\frac{x+1}{3}\right)$$
Veure Solució
Tenim els denominadors 2 i 3. Multipliquem per el seu mínim comú múltiple, 6, per treballar
sense fraccions:
$$ 6\frac{x}{2} + 6\frac{2}{3} = 6\frac{x}{3} + 6 -6\frac{1}{2}\left(1-\frac{x+1}{3}\right)$$
$$ 3x+ 4 = 2x + 6 -3\left(1-\frac{x+1}{3}\right)$$
$$ 3x-2x+ 4 -6 = -3\left(1-\frac{x+1}{3}\right)$$
$$ x -2 = -3\left(1-\frac{x+1}{3}\right)$$
La fracció que queda té un signe negatiu davant, el que implica
canviar el signe del numerador.
Com que el numerador és una suma, canviem el signe d'ambdós sumands:
$$ x -2 = -3\left(1+\frac{-x-1}{3}\right)$$
Calculem la suma en l'interior del parèntesi:
$$ x -2 = -3\left(\frac{3}{3}+\frac{-x-1}{3}\right)$$
$$ x -2 = -3\left(\frac{3-x-1}{3}\right)$$
$$ x -2 = -3\left(\frac{2-x}{3}\right)$$
Tenim el parèntesi multiplicat per 3, però el seu contingut està dividit entre 3, així que podem eliminar els dos 3's:
$$ x -2 = -\left(2-x\right)$$
Llevem el parèntesi canviant el signe dels seus sumands (ja que hi ha un signe menys davant)
$$ x -2 = -2 + x$$
$$ x -x -2 = -2$$
$$ -2 = -2 $$
$$ 0 = 0 $$
Com que tenim una igualtat vertadera, l'equació es compleix independientement dels valors que
prengui x. Per tant, la solució és tots els reals:
$$ x\in \mathbb{R} $$
Equació II.5
$$ 2\left( x - 3\left( x - 4\left( x -\left( \frac{x}{8}+ 1 \right) \right) \right) \right)=1$$
Veure Solució
Tenim múltiples parèntesis niats, alguns amb signe negatiu davant.
Comencem pel més interior: com que té un signe menys, per eliminar-lo canviem el signe
de tots els seus sumands
$$ 2\left( x - 3\left( x - 4\left( x -\frac{x}{8}- 1 \right) \right) \right)=1$$
El més interior està multiplicat per -4. Per eliminar-lo multipliquem per -4 els seus sumands
(multiplicar per 4 i canviar el signe)
$$ 2\left( x - 3\left( x -4x +4\frac{x}{8}+4 \right) \right)=1$$
$$ 2\left( x - 3\left( x -4x +\frac{x}{2}+4 \right) \right)=1$$
$$ 2\left( x - 3\left( -3x +\frac{x}{2}+4 \right) \right)=1$$
De nou, el parèntesi interior està multiplicat per un nombre negatiu:
$$ 2\left( x+ 9x -3\frac{x}{2} -12 \right)=1$$
$$ 2\left( 10x -\frac{3x}{2} -12 \right)=1$$
Llevem l'últim parèntesi:
$$ 20x -2\frac{3x}{2} -24 =1$$
$$ 20x -3x -24 =1$$
$$ 17x =1+24$$
$$ 17x =25$$
$$ x=\frac{25}{17}$$
No podem reduir més la fracció ja que el màxim comú
divisor de 25 i 17 és 1 (perquè 17 és primer).
Equació II.6
$$ x-\frac{2}{3}\left(-1-\left(\frac{15}{2}-x \right)\right)=\frac{x}{3}+1 $$
Veure Solució
Multipliquem tota l'equació per 3 per eliminar algunes de les fraccions:
$$ 3x-2\left(-1-\left(\frac{15}{2}-x \right)\right)=x+3 $$
El parèntesi interior té un signe negatiu davant: canviem el signe de tots els seus sumands
per poder treure-lo:
$$ 3x-2\left(-1-\frac{15}{2}+x \right)=x+3 $$
El parèntesi està multiplicat per -2. Per eliminar-lo, multipliquem els seus sumands per -2 (multiplicar per
2 i canviar el signe):
$$ 3x+2+2\frac{15}{2}-2x =x+3 $$
$$ 3x+2+15-2x =x+3 $$
Ara només cal agrupar els monomis:
$$ 3x-2x -x =3-2 -15 $$
$$ 0 = -14 $$
Obtenim una igualtat falsa, independientement del valor de la incógnita. Açò vol dir que
no hi ha ningún valor per al qual l'equació es compleix: no existeix cap solució.
Equació II.7
$$ \frac{5x}{3} -2 \left( \frac{x}{3}+x \right) =-x $$
Veure Solució
Llevem el parèntesi multiplicant per -2 el seu contingut (multiplicar per 2 i canviar el signe):
$$ \frac{5x}{3} \frac{-2x}{3}-2x = -x $$
Multipliquem tota l'equació per 3 per evitar les fraccions:
$$ 5x -2x-6x = -3x $$
Agrupem els monomis:
$$ 5x -2x-6x +3x= 0 $$
$$ -3x +3x= 0 $$
$$ 0= 0 $$
Obtenim una igualtat que sempre és
certa, independientement del valor de la incógnita. Açò
vol dir que l'equació té infinites solucions: qualsevol valor
és una solució:
$$ x\in \mathbb{R} $$
Part III (12 Equacions)
Equació III.1
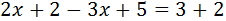
Veure Solució
Sumem (o restem) els monomis que tenen la mateixa part literal
(les x amb les x i els nombres amb els nombres).
Els sumands que estan sumant a un costat passen a l'altre restant i viceversa.
Després passem les x a un costat de la igualtat i els nombres a l'altra.
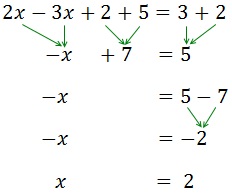
Equació III.2
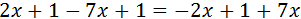
Veure Solució
Els elements que estan sumant a un costat passen a l'altre restant i viceversa.
Després passem les x a un costat de la igualtat i els nombres a l'altra.
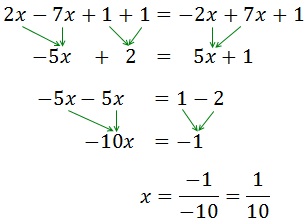
Com que la x té un coeficient (-10) que està multiplicant, aquest passa a l'altre
costat dividint.
Equació III.3
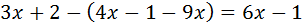
Veure Solució
Primer eliminem el parèntesi: com que té
un signe negatiu davant, canvia el signe a tots els elements que conté.
Després, agrupem les x a un costat i els nombres a l'altre.
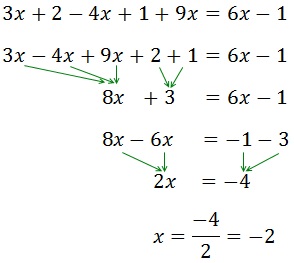
Com que la x té un coeficient (2) multiplicant, aquest passa a l'altre costat dividint.
Equació III.4
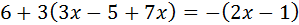
Veure Solució
Primer eliminem els parèntesis: el de la dreta té un signe negatiu que canvia el signe
dels elements del seu interior; com que el de la dreta està multiplicat per 3, multipliquem
els elements que conté per 3.
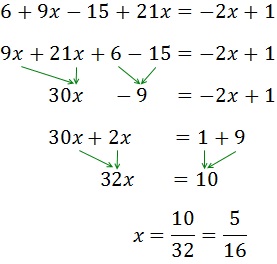
Equació III.5
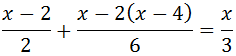
Veure Solució
Tenim fraccions. Podem procedir de diverses maneres:
multiplicar tots els termes de l'equació pel mínim comú
múltiple dels denominadors
o bé, anar multiplicant tota l'equació per cadascun dels denominadors (cada vegada
en desapareix un).
Nosaltres multipliquem tota l'equació pel mínim comú múltiple que és:
$$ mcm(2,2\cdot 3, 3) = 6 $$
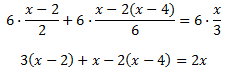
D'aquesta manera, al calcular la divisió, desapareixen tots els denominadors.
Ara eliminem els parèntesis: el primer està multiplicat per 3, així que
multipliquem per 3 el seu contingut; el segon, per -2, així que
multipliquem per -2 (no oblideu el signe):
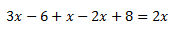
Finalment, agrupem les x a un costat i els nombres a l'altre:
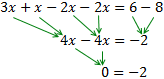
Tenim 0 = -2, que és una igualtat falsa. Per tant, l'equació no té solució perquè sigui quin sigui el valor de x, arribem a un absurd.
Equació III.6
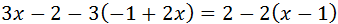
Veure Solució
Com que els nombres que multipliquen els parèntesis són negatius,
al multiplicar el seu contingut per aquests, tots els elements
canvien de signe.
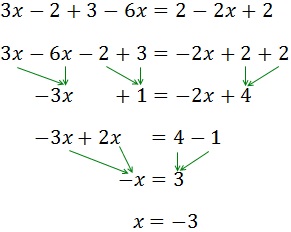
Equació III.7
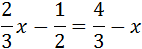
Veure Solució
Com que hi ha denominadors, multipliquem tota l'equació pel mínim comú múltiple d'aquests,
que és 6:
$$ m.c.d.(3,2)=6 $$
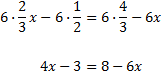
D'aquesta manera, al calcular les divisions, desapareixen els denominadors. Ara només cal agrupar les x a un costat i els nombres a l'altre.
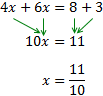
Equació III.8
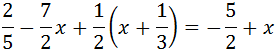
Veure Solució
Com que hi ha denominadors, multipliquem tota
l'equació pel mínim comú múltiple d'aquests, que és 30:
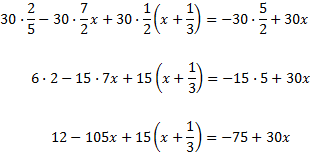
Només hi ha un parèntesi, multiplicat per 15. Per eliminar-lo, multipliquem
els seus elements per 15:
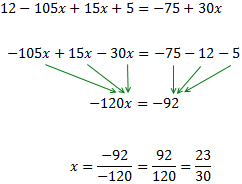
Equació III.9
![equació de primer grau amb parèntesis niats (un dins d'un altre): 4x - (1/3)[15x-3(-1+2x)] = (3/2)(9-x-6) equacions de primer grau resoltes](https://www.matesfacil.com/ESO/Ecuaciones/Ecua9.jpg)
Veure Solució
L'equació té parèntesis niats (uns dins dels altres) i multiplicats per fraccions. Però
abans d'ocupar-nos d'açò, multipliquem tota l'equació pel mínim comú múltiple dels
denominadors: 6
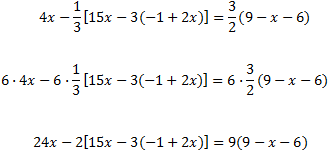
Ara anem a eliminar els parèntesis:
A l'esquerra en tenim dos però, primer treballem amb un i després amb
l'altre. Multipliquem tot el seu contingut per -2.
Al mateix temps, a la dreta, multipliquem per 9:
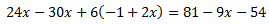
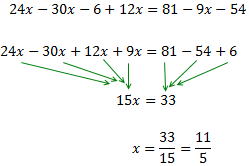
Només queda un parèntesi, multiplicat per 6:
Equació III.10
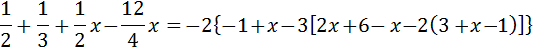
Veure Solució
Com que tenim parèntesis niats (uns dins dels altres), anirem eliminant-los.
El primer parèntesi (l'exterior), està multiplicat per -2. Per eliminar-lo,
multipliquem tot el seu contingut per -2:
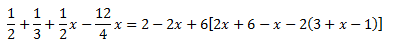
Ara, el parèntesi exterior està multiplicat per 6. Per eliminar-lo, multipliquem
el seu contingut per 6:
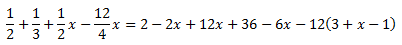
Per últim, el parèntesi que queda està multiplicat per -12, així que multipliquem
per -12 el seu contingut:
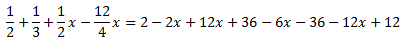
Ara anem a eliminar les fraccions però, abans sumem alguns dels
elements per no tenir una expresió tan llarga:
Multipliquem tota l'equació pel mínim comú múltiple dels denominadors, que és 12:
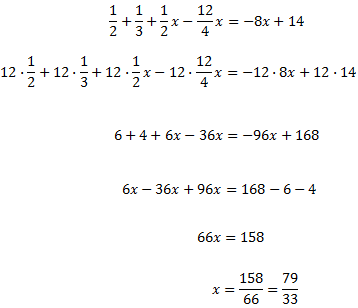
Equació III.11
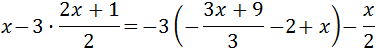
Veure Solució
Hem decidit eliminar primer els parèntesis i, després, multiplicar pels denominadors perquè aquests desapareguin:
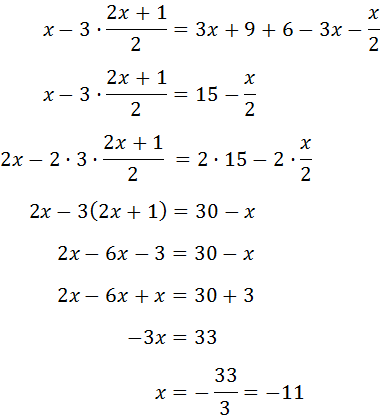
Equació III.12
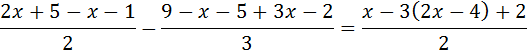
Veure Solució
Aquesta equació consta només de 3 fraccions, així que el que fem és multiplicar-la
pel mínim comú múltiple dels denominadors.
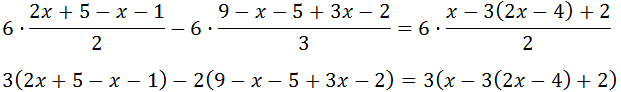

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.

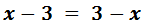
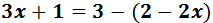
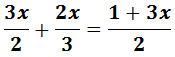
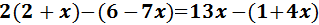
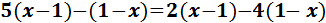
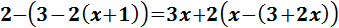
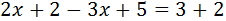
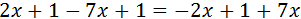
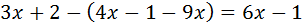
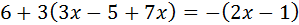
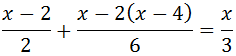
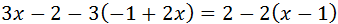
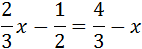
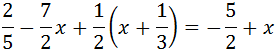
![equació de primer grau amb parèntesis niats (un dins d'un altre): 4x - (1/3)[15x-3(-1+2x)] = (3/2)(9-x-6) equacions de primer grau resoltes](https://www.matesfacil.com/ESO/Ecuaciones/Ecua9.jpg)