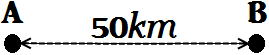Problemes d'Equacions de Primer Grau
Contingut d'aquesta pàgina:
Novetat!
Intel·ligència artificial
Com els algorismes condicionen les nostres vides
Enric Senabre, Vicent Costa
Més informació: sembra llibres.
|
 |
Introducció
Recordem que una equació de primer grau és una igualtat entre dues expressions polinòmiques de grau 1, és a dir, el major grau dels monomis és 1 (o siga, x).
Com que l'equació és de grau 1, hi ha, com a molt, una solució. Diem com a molt perquè també pot ser que no n'hi hagi cap. També està el cas especal de que l'equació sigui una tautologia (per exemple, 0 = 0 ) i aleshores hi ha infinites solucions.
En el següent enllaç es resolen equacions de primer grau: resolució
d'equacions de primer grau.
Sobre els problemes
Els problemes que anem a resoldre són problemes amb els que ens trobem diàriament. La resolució
d'aquests problemes és senzilla si fem ús de les equacions de primer grau (amb una incògnita).
Els exercicis estan ordenats en dificultat creixent, començant per les nocions bàsiques com representar algebraicament el doble d'un nombre, el triple, el consecutiu, etc.
25 Problemes Resolts
Problema 1
Escriure algebraicament les següents expressions:
- El doble d'un nombre.
- El triple d'un nombre.
- El doble d'un nombre més 5.
- El quadrat del triple d'un nombre.
- Les tres quartes parts d'un nombre.
Veure Solució
El doble d'un nombre s'obté al multiplicar-lo per 2, per tant, el doble de x és 2x.
El triple d'un nombre s'obté al multiplicar-lo per 3, per tant, el doble de x és 3x.
El doble de x és 2x, per tant, si li sumem 5, tenim 2x + 5.
El triple de x és 3x, així que el seu quadrat és
$$ (3x)^2 = 3^2 \cdot x^2 = 9x^2 $$
Nota: hem emprat que la potència d'un producte és el producte de
les potències.
La quarta part de x és
$$ \frac{1}{4} \cdot x = \frac{x}{4}$$
Per tant, tres quartes parts de x són
$$ 3\cdot \frac{x}{4} = \frac{3x}{4} $$
Problema 2
Torbar els nombres que compleixen:
- El seu doble més 5 és 35.
- Al sumar-li el seu consecutiu obtenim 51.
- Al sumar el seu doble, la seva meitat i 15, obtenim 99.
- La seva quarta part és 15.
Veure Solució
El doble de x és 2x, llavors obtenim l'equació
$$2x + 5 = 35$$
Resolem l'equació:
$$2x = 35-5$$
$$2x = 30$$
$$x = \frac{30}{2}=15$$
Per tant, el nombre és 15.
-
Sigui x el nombre que busquem, el seu consecutiu (el nombre següent) s'obté
al sumar-li 1. Així, la suma de x i del seu consecutiu és
$$x + ( x + 1 ) = 51$$
Resolem l'equació:
$$2x +1 = 51$$
$$2x = 50$$
$$x = \frac{50}{2} = 25$$
Per tant, el nombre és 25.
El doble de x és 2x i la meitat de x és x/2.
Tenim l'equació:
$$x + 2x + \frac{x}{2} + 15 = 99$$
La resolem:
$$3x + \frac{x}{2} = 99-15$$
$$3x + \frac{x}{2} = 84$$
Hem de sumar fraccions:
$$\frac{6}{2}x + \frac{1}{2}x = 84$$
$$\frac{7}{2}x = 84$$
$$x = \frac{84\cdot 2}{7}=24$$
Per tant, el nombre buscat és 24.
La quarta part de x és x/4. Per tant, volem
$$\frac{x}{4} = 15$$
$$x=15 \cdot 4 = 60$$
El nombre és 60.
Problema 3
Marta té 15 anys, és a dir, la tercera part de l'edat de sa mare. Quina edat té la mare de Marta?
Veure Solució
Anomenem x a l'edat de la mare.
La tercera part de l'edat de la mare és la mateixa que la de Marta, és a dir, 15.
Escrit matemàticament:
$$\frac{x}{3} = 15$$
Per tant, l'edat de la mare és x = 45.
Problema 4
Quant mesura una corda si la seva tercera quarta part mesura 200 metres?
Veure Solució
Sigui x la longitud de la corda. Sabem que la seva tercera quarta part és 200,
és a dir
$$\frac{3x}{4} = 200$$
Per tant, la corda mesura
$$x = \frac{4\cdot 200}{3} = 266.667\ metres. $$
Problema 5
Trobar tres nombres consecutius tals que la seva suma sigui 219.
Veure Solució
Sigui x el primer nombre (el més petit). El nombre següent a aquest és x + 1,
i el següent d'aquest segon és ( x + 1 ) + 1 = x + 2.
Per tant,
$$ x + (x + 1) + (x + 2) = 219$$
$$3x + 3 = 219$$
$$3x = 219-3$$
$$3x = 216$$
$$x = \frac{216}{3} = 72$$
Els nombres són 72, 73 y 74.
Problema 6
Recorrem un camí de 1 km a una velocitat
de 6km/h. Quant de temps
necessitem per arribar al seu final?
Veure Solució
Sabem que l'espai recorregut és igual a la velocitat pel temps.
Sigui x el temps:
Espai recorregut = velocitat · x
Sabem que l'espai és 1km i la velocitat és 6km/h. Substituïm en l'equació:
$$ 1 = 6\cdot x$$
$$ x = \frac{1}{6}$$
Tardem x = 1/6 = 0.1667 hores en arribar.
És a dir,
$$ 0.1667\cdot 60 = 10.002 \ minuts.$$
En realitat, són exactament 10 minuts però, obtenim 10.002 perquè hem aproximat el valor de 1/6.
Nota: no oblidem comprovar les unitats de mesura. Si, per exemple,
l'espai recorregut fos en metres, hauríem de passar-ho a quilòmetres (o canviar
la unitat de la velocitat).
Problema 7
Héctor guarda 25 euros en la seva guardiola,
és a dir, la quarta part dels diners
que ja tenia estalviats. Quants en té en total?
Veure Solució
x = diners que hi havia en la guardiola
25€ són la quarta part del que hi havia, o siga,
$$ 25 = \frac{x}{4}$$
La solució és
$$ x = 25\cdot 4 = 100$$
En la guardiola hi havia 100€. Ara n'hi han
$$ 100 + 25 = 125\ euros$$
Problema 8
El pare d'Ana és 5 anys més jove que sa mare i
la meitat de l'edat d'aquesta és 23. Quina edat
té el pare d'Ana?
Veure Solució
x = edat de la mare d'Ana
La meitat de l'edat de la mare és 23, per tant,
$$ \frac{x}{2} = 23$$
L'edat de la mare és
$$x = 23\cdot 2 = 46$$
El pare d'Ana és 5 anys més jove que sa mare, és a dir, el pare té 46 - 5 = 41 anys.
Problema 9
Carmen té 16 anys i els seus dos
germans en tenen 2 i 3. Quants anys cal que
passen perquè el doble de la suma de las edats dels germans
de Carmen sigui la mateixa que la seva?
Veure Solució
x = anys que han de passar
Quan passen aquests anys, els germans tindran 2 + x el petit i 3 + x
el gran. Així mateix, Carmen tindrà 16 + x anys.
Volem que
$$2( ( 2 + x )+( 3 + x ) ) = 16 + x$$
$$2( 2x + 5) = 16+x$$
$$4x +10 = 16 + x$$
$$4x-x = 16-10$$
$$3x = 6$$
$$x = \frac{6}{3}=2$$
És a dir, han de passar 2 anys.
Problema 10
Donat un nombre, la suma de la seva meitat, el seu doble i el seu triple és 55. Trobar el nombre.
Veure Solució
x = nombre que busquem
x/2 és la seva meitat
2x és el seu doble
3x és el seu triple
Volem que
$$\frac{x}{2} + 2x + 3x = 55$$
$$\frac{x}{2} + 5x = 55$$
$$\frac{1}{2}x + \frac{10}{2}x = 55$$
$$\frac{11}{2}x = 55$$
$$x = \frac{55 \cdot 2}{11}=10$$
Per tant, el nombre és 10.
Problema 11
Vicent es gasta 20 euros en uns
pantalons i una camisa. No sap el preu de cada peça però,
sí que sap que la camisa val dues quintes parts
del que valen els pantalons. Quin és
el preu dels pantalons?
Veure Solució
x = preu dels pantalons
La camis val 2/5x.
Sabem que el total són 20€, per tant,
$$x + \frac{2}{5}x = 20$$
$$\frac{5}{5}x + \frac{2}{5}x = 20$$
$$\frac{7}{5}x = 20$$
$$x = \frac{20 \cdot 5}{7} = \frac{100}{7}=14,2857$$
Els pantalons valen 14,29€.
Problema 12
La diferència entre dos nombres és 17 i el doble
del menor d'aquests és 26. Quins nombres
són? I si 26 és el doble del més gran, quins
nombres són?
Veure Solució
Primera part:
x = nombre petit
La diferència entre els dos és 17, llavors el gran és x + 17.
El doble del petit és 26, llavors 2x = 26, és a dir, x = 13.
Els nombres són 13 i 13 + 17 = 30.
Segona part:
x = nombre gran
La diferència entre els dos és 17, llavors el petit és x - 17.
El doble del gran és 26, llavors 2x = 26, és a dir, x = 13.
Els nombres són 13 i 13 - 17 = - 4.
Problema 13
Fa 5 anys, l'edat d'Ernest era el triple que la
del seu cosí Joan, que ara en té 15. Quants anys han
de passar perquè Joan tingui l'edat actual d'Ernest?
Veure Solució
x = edat actual d'Ernest
Fa 5 anys Ernest tenia x - 5 anys i Joan en tenia 10.
Fa 5 anys, l'edat d'Ernest, x - 5, era el triple que la de Joan, és a dir,
$$x - 5 = 3\cdot 10$$
Per tant, x = 30 + 5 = 35
Ernest té ara 35 anys.
Joan tindrà 35 anys d'aquí a 35 - 15 = 20 anys.
Problema 14
Tenim tres peixeres i 56 peixos. Les mesures de les peixeres són: petita, mitjana i gran, sent la petita exactament la meitat que la mitjana i la gran, el doble.
Com que no tenim ninguna preferència a l'hora de repartir els peixos, decidim que
en cadascuna de les peixeres hi haurà una quantitat de peixos proporcional a la seua mesura.
Calcular quants peixos hi ha d'haver en cadascuna de les peixeres.
Veure Solució
x = nombre de peixos en la peixera mitjana
x/2 = nombre de peixos en la peixera petita
2x =nombre de peixos en la peixera gran
Com que el total de peixos és 56, tenim l'equació de primer grau
$$x + \frac{x}{2} + 2x = 56$$
Resolem:
$$3x + \frac{x}{2} = 56$$
Tenim que sumar les fraccions:
$$\frac{6x}{2} + \frac{x}{2} = 56$$
$$\frac{7x}{2} = 56$$
La solució és
$$x = \frac{56\cdot 2}{7}= 16$$
Peixos en la peixera petita: 16/2 = 8
Peixos en la peixera mitjana: 16
Peixos en la peixera gran: 2·16 = 32
Problema 15
Volem repartir 510 caramels entre un grup de
3 xiquets, de manera que dos d'aquests
tinguin la meitat dels caramels però que un d'aquests dos
tingui la meitat que l'altre. Quants caramels tindrà cadascun?
Veure Solució
La quantitat de caramels de dos d'ells és la meitat del total, per la qual
cosa l'altre xiquet tindrà l'altra meitat, és a dir, el tercer xiquet tindrà 510/2 = 255
caramels.
Ara resten els 255 caramels a repartir entre els dos primers.
x = nombre de caramels de un dels dos primers xiquets, suposem que
és el que té la major quantitat
L'altre xiquet té la meitat de x, és a dir, x/2.
La suma dels caramels dels dos és 255, llavors tenim l'equació
$$ x + \frac{x}{2} = 255$$
Sumem les fraccions
$$ \frac{3x}{2} = 255 $$
$$ x = \frac{255\cdot 2}{3} = 170$$
Un en té 170 i l'altre en té 170/2 = 85.
Les quantitats de caramels de cada xiquet són: 255, 170 i 85.
Problema 16
La tercera part de les culleres de la casa estaven al
rentaplats i la resta al calaix. Més tard, la meitat de
les culleres del calaix, 15, es porten a la taula.
Quantes culleres hi ha al rentaplats?
Veure Solució
x = total de culleres
Al rentaplats hi ha la tercera part del total, és a dir:
$$\frac{x}{3}$$
Les restants estaven, al principi, al calaix. Al calaix hi havia
$$ \frac{2x}{3}$$
La meitat de las que hi havia al calaix és 15. És a dir, al calaix hi havia 30 culleres.
Igualant a 30 l'expressió anterior:
$$ \frac{2x}{3} = 30 $$
D'on obtenim que
$$x = \frac{30\cdot 3}{2} = 45$$
Hi ha un total de 45 culleres. D'aquestes 45, 15 es troben al rentaplats.
De les 30 restants, 15 estan a la taula i altres 15 al calaix.
Problema 17
Una botiga ven en dos dies la tercera part dels seus productes.
L'endemà, rep del magatzem la meitat de la quantitat
dels productes venuts, que són 15
unitats.
Quantes unitats vengué en els dos primers dies?
Quantes unitats hi ha en la botiga després
de l'abastament?
Veure Solució
x = nombre inicial de productes
En els dos primers dies es venen
$$\frac{x}{3}$$
L'endemà es rep la meitat de la quantitat venuda que és 15, és a dir, tenim l'equació
$$\frac{1}{2}\cdot \frac{x}{3} = 15 $$
Hem multiplicat per 1/2 per obtenir la meitat.
Resolem l'equació:
$$ \frac{x}{6} = 15$$
$$ x = 15 \cdot 6 = 90$$
A la botiga hi havia 90 productes.
En els dos primers dies es venen
$$\frac{x}{3} = \frac{90}{3} = 30$$
La quantitat despés de la venta i de l'abastament és: 90 - 30 + 15 = 75 productes.
Problema 18
Joan té 400 euros i Rosa en té 350. Tots dos es compren el mateix llibre. Després de la compra, a Rosa li queden cinc sisenes parts dels diners que li queden a Joan.
Calcular el preu del llibre.
Veure Solució
x = preu del llibre
Diners que li queden a Joan: 400 - x
Diners que li queden a Rosa: 350 - x
Ell diners que li queden a Rosa és 5/6 dels que li queden a Joan, per tant,
$$ 350 - x = \frac{5}{6}( 400 - x )$$
Multipliquem per 6
$$ 2100 - 6x = 5(400-x) $$
$$ 2100 - 6x = 2000 -5x $$
$$ 2100 - 2000 = 6x -5x$$
$$ 100 = x$$
El preu del llibre és 100€
Problema 19
Ester té el triple de diners que Ana i la meitat que Héctor. Héctor els dóna a Ana i a Ester 25 euros a cadascuna. Ara Ester té la mateixa quantitat que Héctor. Quants diners tenia cadascun i quants en tenen ara?
Veure Solució
x = quantitat inicial de diners d'Ana
La quantitat inicial d'Ester és el triple que la d'Ana, és a dir, Ester tenia 3x
La quantitat inicial d'Héctor és el doble que la d'Ester, per tant, Héctor tenia 2·3x = 6x
Es fa el repartiment:
Héctor té 50€ menys, és a dir, Héctor té 6x - 50
Ana té 25€ més, és a dir, Ana té x + 25
Ester té 25€ més, és a dir, Ester té 3x + 25
Ara Ester té la mateixa quantitat que Héctor, és a dir, 3x + 25 = 6x - 50.
Equació que té la solució x = 25.
Inicialment tenien:
Ester: 3·25 = 75€
Ana: 25€
Héctor: 6·25 = 150€
Després del repartiment:
Ester: 75 + 25 = 100€
Ana: 25 + 25 = 50€
Héctor: 150 - 25 = 100€
Problema 20
El dipòsit d'aigua d'una casa es troba al 2/7 de
la seva capacitat. Es dutxen tres persones: el primer en
dutxar-se consumeix una cinquena part de la quantitat
d'aigua que hi ha; el segon, una tercera part de la
quantitat que queda; i el tercer, tres quartes parts de
la quantitat del primer.
Quina és la capacitat del dipòsit i la quantitat d'aigua
que consumeixen els dos primers si sabem que el
tercer consumeix 10 litres?
Veure Solució
x = capacitat del dipòsit
Abans de dutxar-se, el dipòsit es troba al 2/7, és a dir, hi ha
$$\frac{2}{7}x \ litres$$
El primer consumeix 1/5 de l'aigua que hi ha en el depòsit, és a dir, consumeix
$$\frac{1}{5} \cdot \frac{2}{7}x = \frac{2}{35}x$$
Com que el primer consumeix
$$\frac{1}{5} \cdot \frac{2}{7}x$$
després de dutxar-se resten
$$\frac{4}{5} \cdot \frac{2}{7}x = \frac{8}{35}x$$
pel que el segon consumeix
$$\frac{1}{3} \cdot \frac{8}{35}x = \frac{8}{105}x$$
El tercer consumeix 3/4 del que consumeix el primer, és a dir, consumeix
$$\frac{3}{4} \cdot \frac{2}{35}x = \frac{3}{70}x$$
El tercer consumeix 10L, per tant,
$$\frac{3}{70}x = 10$$
és a dir,
$$x = \frac{700}{3}$$
La capacitat del depòsit és de 700/3 = 233.33 litres.
El primer consumeix 2/35·700/3 = 40/3 = 13.33 litres.
El segon consumeix 8/105·700/3 = 160/9 = 18.77 litres.
Problema 21
Quant es tarda en recórrer una distància de 10km a una velocitat de 40 km/h?
Veure Solució
Sabem que l'espai recorregut és la velocitat pel temps, és a dir,
$$ e = v\cdot t $$
Les dades que tenim són
$$e = 10km,\ v=40km/h$$
Com que tenim les mateixes unitats (km), només
cal substituir en l'equació i aïllar la
t, que estarà donada en hores (h).
$$ 10 = 40\cdot t$$
Resolem l'equació:
$$ t= \frac{10}{40} =\frac{1}{4} = 0.25h$$
Podem passar el temps a minuts (multiplicant per 60):
$$ t = 0.25\cdot 60 = 15 min$$
Nota: podem escriure les unitats en l'equació
i tractar-les com a altres factors. D'aquesta manera, quan tenim
una gran quantitat i varietat d'unitats, és més fàcil saber quina
és la unitat del resultat:
$$10km = \frac{40km}{h}\cdot t $$
Aïllem la t:
$$ t = \frac{10km}{40km}h$$
I ara, com que km està multiplicant en el numerador i en el denominador,
el podem eliminar:
$$ t = \frac{10}{40}h= \frac{1}{4}h = 0.25h = 15min$$
Problema 22
Quants minuts es tarda en recórrer una distancia de 108km a
una velocitat de 120m/h?
Veure Solució
L'espai recorregut és la velocitat pel temps, és a dir,
$$ e = v\cdot t $$
Com que volem saber el temps, t, anem a aïllar la t abans de substituir les
dades en l'equació:
$$ e = v\cdot t \ \rightarrow \ t =\frac{e}{v} $$
Tenim les dades
$$ e=108km,\ v=120m/h $$
Tenim les unitats en quilòmetres (km) i
metres (m), així que hem de passar-les a una mateixa unitat.
Escriurem la velocitat en km/min. D'aquesta manera,
tenim km en ambdues dades
i, amés, obtindrem el temps en minuts.
$$ v = \frac{120m}{h} = \frac{120:1000km}{60min} $$
Nota: hem dividit per 1000 per
passar de metres a quilòmetres
i multiplicat per 60 per passar d'hores a minuts. Fent els càlculs:
$$ v = \frac{0.12 km}{60min} \simeq 0.002 km/min$$
Ara substituïm les dades i obtenim el temps
$$ t = \frac{e}{v} = \frac{108km}{0.002km/min} = 54000\ min $$
Nota: como que min està dividint en el
denominador, passa multiplicant
en el numerador; km desapareix perquè està multiplicant
en el numerador i en el
denominador.
Problema 23
Quants quilòmetres es recorren si es circula a una velocitat constant
de 5m/s durant dues hores?
Veure Solució
L'espai recorregut és la velocitat pel temps, és a dir,
$$ e = v\cdot t $$
Coneixem les dades
$$ v=5m/s,\ t=2h $$
Tenim distintes unitats de temps. Passem el temps a segons:
$$ t=2h = 2\cdot 60 min = 120min = 120\cdot 60 s =7200 s $$
No passem encara els m a km per no treballar amb decimals.
Finalment, substituïm en l'equació i passem a km:
$$ e = v\cdot t = \frac{5m}{s} \cdot 7200s = 36000m =36km$$
Problema 24
En una marató de 45km, el guanyador corregué a una velocitat mitjana de
16km/h, mentre que l'últim en arribar ho va fer a una mitjana
de 7.5km/h.
Quant tardaren en arribar a la meta cadascun d'ells?
Veure Solució
L'espai recorregut és la velocitat pel temps, és a dir,
$$ e = v\cdot t $$
Com que volem saber el temps, t, anem a aïllar la t abans de substituir les
dades en l'equació:
$$ e = v\cdot t \ \rightarrow \ t =\frac{e}{v} $$
Substituïm les dades per al guanyador:
$$ t= \frac{45km}{16km/h} = 2.81h \simeq 2h\ 48min $$
Per escriure el temps en hores i en minuts hem fet el següent:
$$2.81h = 2h +0.81h = 2h + 0.81\cdot 60min \simeq 2h\ 48min$$
Substituïm les dades per al últim classificat:
$$ t= \frac{48km}{7.5km/h} = 6h$$
Per tant, el guanyador tardà 2h 48min i l'últim tardà 6h.
Problema 25
La distància entre les ciutats A i B és de 50km. A la mateixa hora surt un camió de la ciutat A a 60km/h i un ciclista de la ciutat
B a 25km/h.
Es vol calcular quant tardaran en trobar-se si ambdós
vehicles circulen per la mateixa carretera però en sentit oposat.
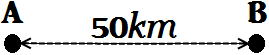
Veure Solució
Tenim les dades inicials:
Quan els dos vehicles es troben, el camió ha recorregut una distància
major que el ciclista (ja que la seua velocitat és major). Com que
no coneixem aquesta
distància, l'anomenarem x. Així mateix, el ciclista haurà recorregut 50 - x km.
L'esquema del problema és
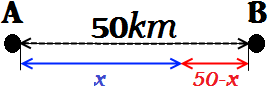
A les dades inicials tenim que afegir l'espaio recorregut pel camió
$$ e_c=x $$
i el recorregut per la bicicleta
$$ e_b = 50-x$$
Els temps són els mateixos ja que ambdós vehicles surten en el mateix instant:
$$ t_c = t_b $$
Substituïm en l'equació les dades del camió:
$$ e_c=v_c \cdot t_c $$
$$ x=60\cdot t_c $$
$$ t_c = \frac{x}{60}$$
D'altra banda, si substituïm les dades de la bicicleta tenim
$$ e_b=v_b \cdot t_b $$
$$ 50-x=25\cdot t_b $$
$$ t_b = \frac{50-x}{25}$$
Però, com ja hem dit abans, els temps són el mateix i, per tant,
podem igualar-los obtenint una equació de primer grau:
$$ t_c = t_b $$
$$ \frac{x}{60} = \frac{50-x}{25} $$
Resolem l'equació:
$$ 25x = 3000 - 60x$$
$$ 85x = 3000$$
$$ x = \frac{3000}{85} \simeq 35.3$$
Per tant, quan es troben, el camió ha recorregut
uns 35.3km i el ciclista 50 - 35.3 = 14.7 km.
Com que volem saber el temps, substituïm en qualsevol de
les dues equacions que tenim:
$$ t_c = \frac{x}{60} = \frac{35.3 km}{60km/h} \simeq $$
$$ \simeq 0.59h = 35.4min$$

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.