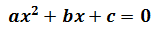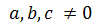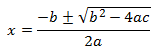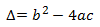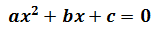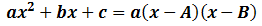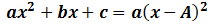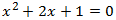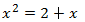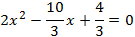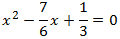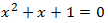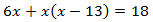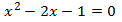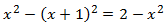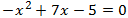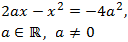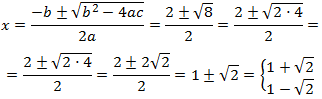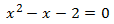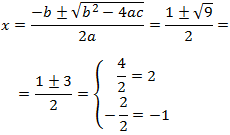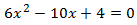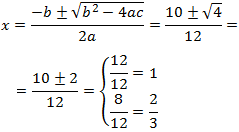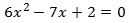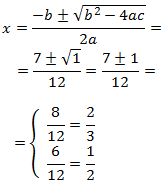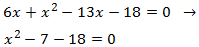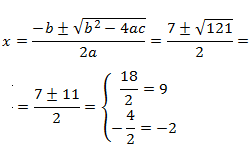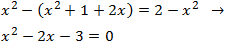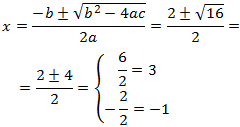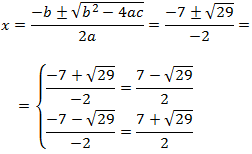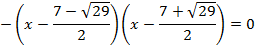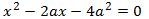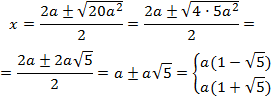Equacions de Segon Grau Completes |
|
Contingut d'aquesta pàgina:
Breu introducció
-
Recordem que... la fórmula quadràtica, el discriminant i factorització
-
10 Equacions resoltes i demostració de la fórmula quadràtica
Novetat!
Intel·ligència artificial
Com els algorismes condicionen les nostres vides
Enric Senabre, Vicent Costa
Més informació: sembra llibres.
|
 |
Introducció
En aquesta secció anem a calcular les arrels (solucions) d'equacions de segon grau
completes. Per a això, farem servir la fórmula quadràtica que ens proporciona les solucions. A més, escriurem l'equació en forma factorizada a partir de les arrels.
Pàgines relacionades: equacions de segon grau incompletes.
Recordem que...
Una equació de segon grau és una equació polinòmica de grau 2, és a dir, el major grau dels monomis és 2, o siga, x2. Com que l'equació és de
grau 2, tindrà, com a molt, dues arrels (solucions) distintes.
Tota equació de segon grau es pot escriure en la forma
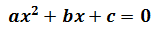
Si ningun dels coeficients, a,b i c és zero, és a dir,
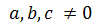
direm que l'equació és completa. Si no és així (si b ó c és 0), direm que és incompleta.
Solucions i discriminant
Les solucions ( o arrels) de l'equació de segon grau venen donades per la fórmula quadràtica:
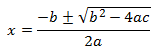
Anomenem discriminant de l'equació al radicant de la fórmula anterior, o siga, a
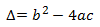
Es compleix que
-
Si Δ = 0, l'equació té una única solució (de multiplicitat 2)
-
Si Δ < 0, no existeixen solucions (reals)
-
Si Δ > 0, existeixen dues solucions (reals) distintes (de multiplicitat 1).
Factorització
Factoritzar una equació consisteix en expressar-la com un producte de polinomis més simples, és a dir, com un producte de polinomis de grau menor.
Per exemple:
$$x^2 + 2x + 1 = (x + 1)(x + 1)$$
-
Suposem que A i B són les dues solucions de l'equació
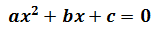
Aleshores, podem escriure el polinomi corresponent a l'equació com
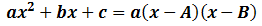
-
Si la única solució és A (per tant, de multiplicitat 2), la factorització és
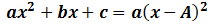
-
Si no hi ha solucions, no podem factoritzar-la.
10 Equacions Resoltes
Equació 1
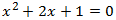
Veure solució
El discriminant és
$$ \Delta = b^2 - 4ac =$$
$$= (-2)^2 - 4\cdot \cdot 1 \cdot (-1) =$$
$$ = 4 + 4 = 8 > 0 $$
Per tant, l'equació té dues arrels simples. Apliquem la fórmula:
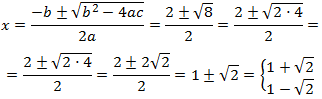
Per tant, les solucions són
$$ x = 1 - \sqrt{2},\ 1 + \sqrt{2} $$
I una factorització de l'equació és
$$ (x - 1 + \sqrt{2} )\cdot ( x - 1 - \sqrt{2} ) = 0 $$
Equació 2
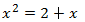
Veure solució
Escrivim l'equació en la forma general:
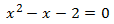
El discriminant és
$$ \Delta = b^2 - 4ac =$$
$$= (-1)^2-4\cdot 1\cdot (-2) =$$
$$ = 1 + 8 = 9 > 0 $$
Per tant, l'equació té dues arrels simples. Apliquem la fórmula:
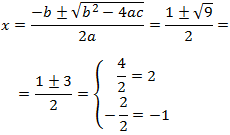
Les dues solucions són \(x = -1, 2\).
I una factorització de l'equació és
$$ (x+1)(x-2) = 0 $$
Equació 3
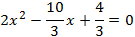
Veure solució
Multipliquem per 3 l'equació per evitar les fraccions (açò no canvia les solucions):
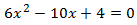
El discriminant de l'equació és
$$ \Delta = b^2 -4ac =$$
$$ = (-10)^2 -4\cdot 6\cdot 4 =$$
$$ 100-96 = 4 > 0 $$
Per tant, l'equació té dues arrels simples. Apliquem la fórmula
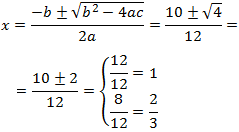
Les solucions són \(x = 1, 2/3\).
I una factorització de l'equació és
$$ 2(x-1)(x-\frac{2}{3}) = 0 $$
Recordem que tenim que multiplicar pel coeficient director de l'equació original
en la factorització (si volem que l'expressió polinòmica sigui la mateixa).
Equació 4
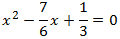
Veure solució
Multipliquem l'equació per 6 per evitar les fraccions:
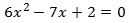
El discriminant de l'equació és
$$ \Delta = b^2 - 4ac =$$
$$ = (-7)^2 - 4\cdot 6\cdot 2 =$$
$$ = 49 - 48 = 1 > 0 $$
Per tant, té dues arrels simples. Apliquem la fórmula:
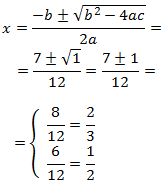
Les solucions són \( x = 2/3, 1/2\).
I una factorització de l'equació és
$$ \left(x-\frac{2}{3} \right)\left(x-\frac{1}{2} \right) = 0 $$
Equació 5
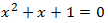
Veure solució
El discriminant és
$$ \Delta = b^2 - 4ac =$$
$$ = 1^2 - 4\cdot 1\cdot 1 =$$
$$ = 1 - 4 = - 3 < 0$$
Per tant, l'equació no té solucions reals i no podem factoritzar-la.
Equació 6
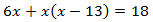
Veure solució
Escrivim l'equació en la forma general:
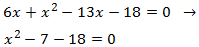
El discriminant és
$$ \Delta = b^2 - 4a c =$$
$$ = (-7)^2 -4\cdot 1\cdot (-18) =$$
$$ = 49 + 74 = 121 > 0 $$
Per tant, l'equació té dues arrels simples. Apliquem la fórmula:
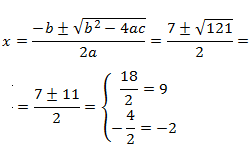
les solucions són \(x = -2, 9\).
I una factorització de l'equació és \((x-9)(x+2) = 0\).
En aquesta factorització multipliquem per 1 perquè és el coeficient de l'última equació que tenim, no el de la
inicial ja que aquesta no està en la forma general.
Equació 7
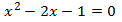
Veure solució
L'equació està escrita en forma general.
El discriminant és
$$ \Delta = b^2- 4ac =$$
$$ = (-2)^2 -4\cdot 1\cdot (-1) =$$
$$ = 4 + 4 = 8 > 0 $$
Per tant, l'equació té dues arrels simples. Apliquem la fórmula:
$$ x = \frac{2 \pm \sqrt{8}}{2} = $$
$$ = \frac{2 \pm 2 \sqrt{2}}{2} = $$
$$ = 1 \pm \sqrt{2} $$
Per tant, les solucions són:
$$ x = 1 +\sqrt{2},\ 1 - \sqrt{2} $$
I una factorització de l'equació és
$$ (x-1- \sqrt{2})(x-1+\sqrt{2}) = 0 $$
Equació 8
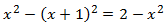
Veure solució
Escrivim l'equació en la forma general. Recordem la fórmula del binomi (quadrat de la resta):
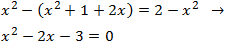
El discriminant és
$$ Δ = b^2 - 4ac =$$
$$ =(-2)^2 -4\cdot 1 \cdot (-3) =$$
$$ = 4 + 12 = 16 > 0
Per tant, l'equació té dues arrels simples. Apliquem la fórmula:
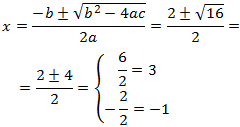
Les solucions són \(x = 3, -1\).
I una factorització de l'equació és
$$ (x-3)(x+1) = 0 $$
Equació 9
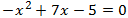
Veure solució
El discriminant és
$$ \Delta = b^2- 4ac =$$
$$= 7^2 -4(-1)(-5) =$$
$$ = 49 - 20 = 29 > 0 $$
Per tant, l'equació té dues solucions simples. Apliquem la fórmula:
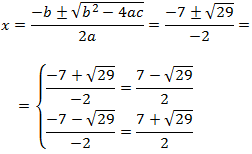
La factorització de l'equació és
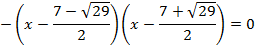
Equació 10
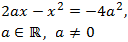
Veure solució
En aquesta equació tenim un paràmetre. Suposem que a > 0 per evitar
l'ús del valor absolut (per qüestions tècniques).
Escrivim l'equació en la forma general:
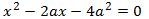
El discriminant és
$$ \Delta =(-2a)^2-4\cdot 1\cdot (-4a^2) =$$
$$ = 4^2+ 16a^2 = 20a^2 > 0$$
Per tant, l'equació té dues arrels simples. Apliquem la fórmula:
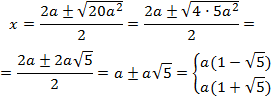
Una factorització és
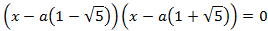
Demostració de la Fórmula
Demostrar que, en efecte, la fórmula
$$x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$$
proporciona les arrels de l'equació general de segon grau
$$ax^2+bx+c=0$$
Demostrar que són solucions però no demostrar la unicitat
(és a dir, no demostrar que són exactament les úniques dues solucions).
Veure solució
Si substituïm en l'equació , obtindrem una expressió llarga.
Sabem que si A i B són les solucions de l'equació , aleshores
podem escriure-la com
$$ax^2 +bx +c = a(x-A)(x-B)$$
El que anem a fer és comprovar aquesta igualtat. Les solucions A
i B són les
que ens proporciona la fórmula quadràtica. Així,
$$a(x-A)(x-B) =$$
$$=a\left( x-\frac{-b - \sqrt{b^2-4ac}}{2a}\right) \left( x-\frac{-b + \sqrt{b^2-4ac}}{2a}\right)=$$
$$= a\left( x+\frac{b}{2a}+\frac{\sqrt{b^2-4ac}}{2a}\right) \left( x+\frac{b}{2a}-\frac{\sqrt{b^2-4ac}}{2a}\right) $$
Tenim una suma per diferència, és a dir, aplicarem la fórmula
$$(a+b)(a-b)=a^2-b^2 $$
Continuem:
$$= a\left( \left( x+\frac{b}{2a}\right) ^2 - \left( \frac{\sqrt{b^2-4ac}}{2a}\right) ^2 \right) =$$
$$= a\left( x^2 +2x\frac{b}{2a}+\frac{b^2}{4a^2}\right) - a\left( \frac{b^2-4ac}{4a^2} \right)=$$
$$= ax^2 +bx+\frac{b^2}{4a} - \frac{b^2-4ac}{4a} =$$
$$= ax^2 +bx+\frac{b^2 -b^2+4ac}{4a} =$$
$$= ax^2 +bx+\frac{4ac}{4a} =$$
$$= ax^2 +bx+ c $$

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.