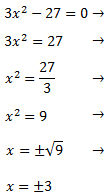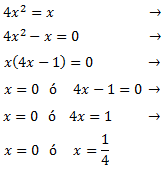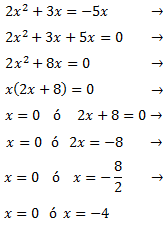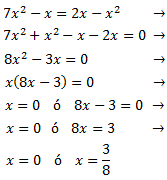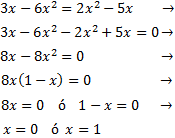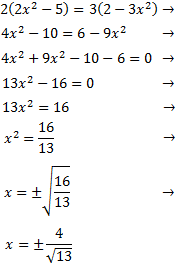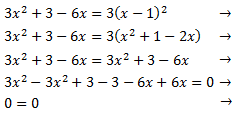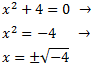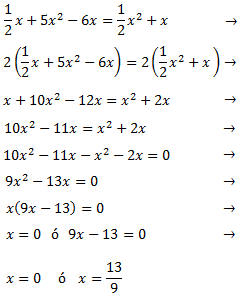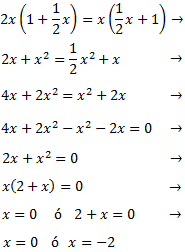Equacions de Segon Grau Incompletes

Contingut d'aquesta pàgina:

• Breu introducció

• Mètode per obtenir les solucions

• 10 Equacions Resoltes

Novetat! Intel·ligència artificial Com els algorismes condicionen les nostres vides Enric Senabre, Vicent Costa Més informació: sembra llibres.

---

Introducció

Anem a resoldre equacions de segon grau incompletes dels tres tipus. També, anem a fer ús de les arrels de l'equació per escriure aquesta com un producte (factoritzar).

Recordem que una equació de segon grau, completa o no, pot tenir, com a màxim, dues arrels (solucions) distintes. Aquí podem accedir a la secció d'equacions de segon grau completes.

Una equació de segon es pot escriure en la forma

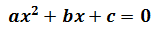
direm que l'equació és completa quan ningun dels coeficients, a,b i c és zero, és a dir,

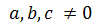
I direm que és incompleta quan algun dels coeficients b ó c és zero, és a dir,

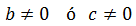
Per tant, una equació incompleta té alguna de les següents formes

---

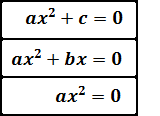
Obtenció de les arrels (solucions)

• Si és de la forma

  

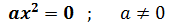
  Tenim la única solució (arrel doble) x = 0.

• Si és de la forma

  

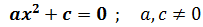
  Aïllem x i tenim que

  

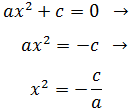
  Les dues arrels són

  

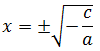
  Però és necessari que el radicant (l'interior de l'arrel) sigui positiu. Si no és així, no existeixen solucions (reals).

• Si és de la forma

  

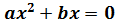
  Factoritzem

  

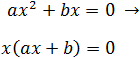
  Com que és un producte amb resultat 0, algun dels dos factors ha de ser 0. Per tant, tenim les possibilitats (arrels):

  

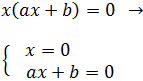
  Notem que en el segon cas la solució és

  $$ x = - \frac{b}{a} $$

---

---

10 Equacions Resoltes

---

Equació 1

---

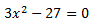
Equació 2

---

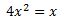
Equació 3

---

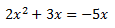
Equació 4

---

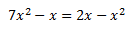
Equació 5

---

---

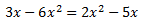
Equació 6

---

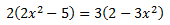
Equació 7

---

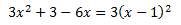
Equació 8

---

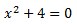
Equació 9

---

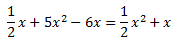
Equació 10

---

---

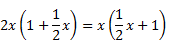
Matesfacil.com by J. Llopis is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.