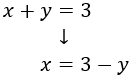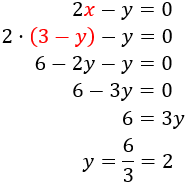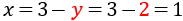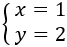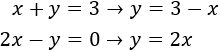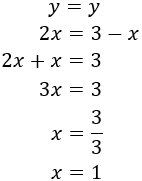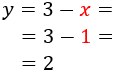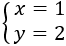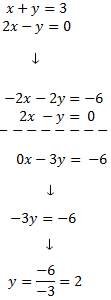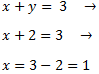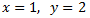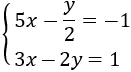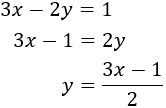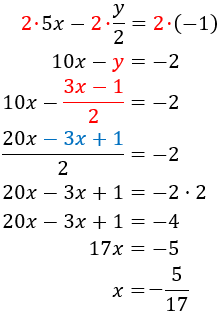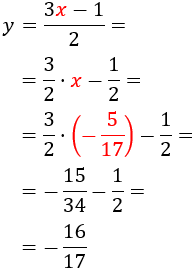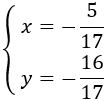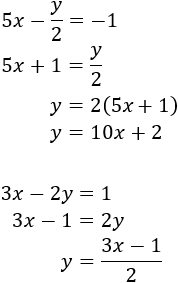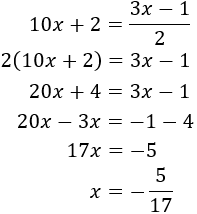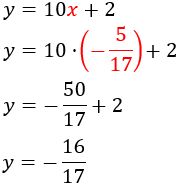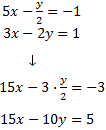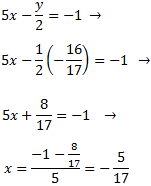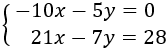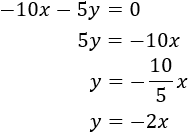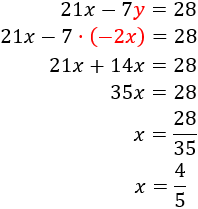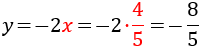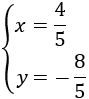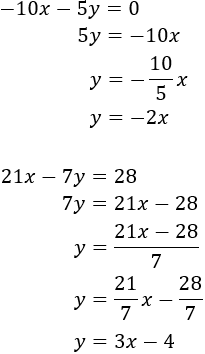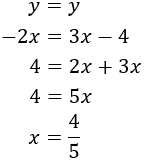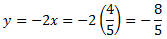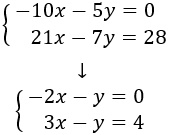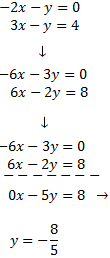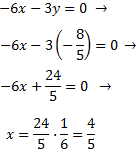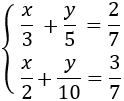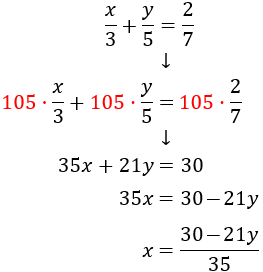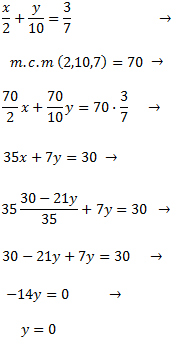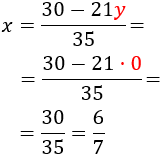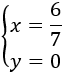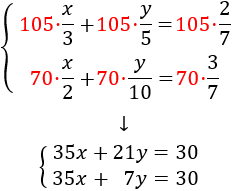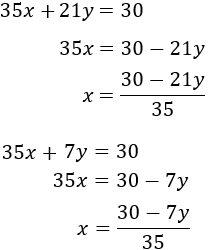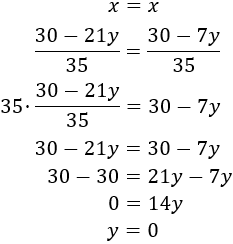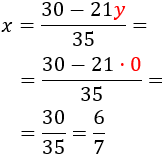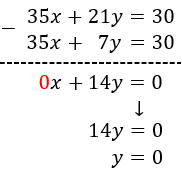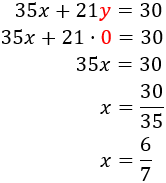Sistemes d'equacions: substitució, igualació i reducció |
Contingut d'aquesta pàgina:
Breu introducció.
Resolució de sistemes d'equacions per substitució, igualació i reducció.
Pàgines relacionades: Problemes de Sistemes d'Equacions
Novetat!Intel·ligència artificialCom els algorismes condicionen les nostres videsEnric Senabre, Vicent Costa Més informació: sembra llibres. |
 |
Introducció
Un sistema d'equacions lineals és un conjunt d'equacions (lineals) que tenen més d'una incògnita. Les incògnites apareixen en diverses de les equacions però, no necessàriament en totes. El que fan aquestes equacions és relacionar les incògnites entre elles.
Per exemple:
$$\left\{ \begin{eqnarray} 3x+2y=1 \\ x-5y=6 \end{eqnarray} \right. $$Es tracta d'un sistema de dues equacions amb dues incògnites (x i y).
Resolre aquest tipus de problemes (un sistema) consisteix en trobar el valor per a cada incògnita de manera que es compleixin totes les equacions del sistema alhora.
La solució del sistema de l'exemple és
$$ \begin{eqnarray} x=1 \\ y=-1 \end{eqnarray}$$Però, no sempre existeix solució, o bé en poden existir infinites. Si hi ha una única solució (un valor per a cada incògnita, com en l'exemple anterior) es diu que el sistema és compatible determinat. No parlarem dels altres tipus ja que en aquesta secció només s'estudien els sistemes determinats.
Per resoldre un sistema (compatible determinat) necessitem tenir al menys tantes equacions com incògnites (i han de ser linealment independents).
Anem a resoldre sistemes de dues equacions amb dues incògnites pels tres mètodes bàsics que descrivim a continuació i que es basen en l'obtenció i resolució d'una equació de primer grau.
-
Substitució: consisteix en aïllar una de les incògnites (per exemple x) i substituir la seva expressió en l'altra equació. D'aquesta manera, obtindrem una equació de primer grau amb l'altra incògnita, y. Una vegada resolta l'equació, obtenim el valor de x fent ús del valor de y que ja coneixem.
-
Reducció: consisteix en operar amb les equacions com, per exemple, sumar o restar ambdues equacions, de manera que una de les incògnites desaparegui. Així, obtenim una equació amb una sola incògnita.
-
Igualació: consisteix en aïllar en ambdues equacions la mateixa incògnita per poder igualar les expressions, obtenint així una equació amb una sola incògnita.
No oblidem que si multipliquem una equació per un nombre distint de 0, l'equació inicial i l'obtesa són equivalents. Açò vol dir que ambdues equacions tenen les mateixes solucions i, per tant, podem treballar amb una o altra. Farem servir aquesta propietat amb freqüència al mètode de reducció.
| Sistemes resolts (click per veure solució) | |||
|---|---|---|---|
| 1 |
| ||
| 2 |
| ||
| 3 |
| ||
| 4 |
| ||