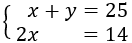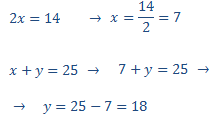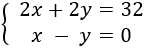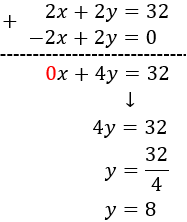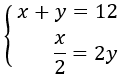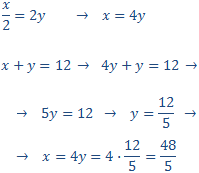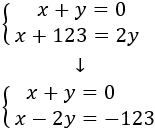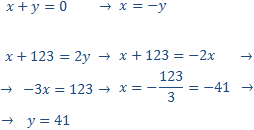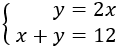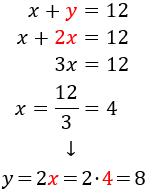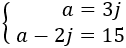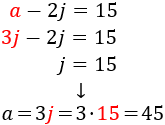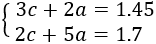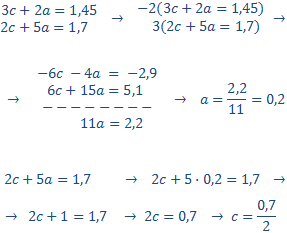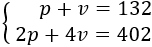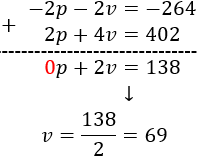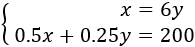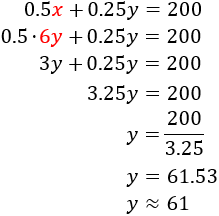Problemes amb Sistemes d'Equacions
|
Contingut d'aquesta pàgina:
Novetat!
Intel·ligència artificial
Com els algorismes condicionen les nostres vides
Enric Senabre, Vicent Costa
Més informació: sembra llibres.
|
 |
Introducció
Un sistema d'equacions és un conjunt d'equacions (en el nostre cas seran dues equacions) i diverses
incògnites (en el nostre cas en seran dues) que apareixen en una o diverses de les equacions.
Una equació que té més d'una incògnita ens informa de la relació que existeix
entre aquestes. Per exemple, l'equació x - y = 0 ens diu que x i y són el
mateix nombre.
No podem resoldre aïlladament una equació amb dues incògnites ja que una d'elles queda en funció de l'altra. Per
exemple, si tenim l'equació x - 2y = 0 i aïllem x obtenim que x = 2y. És a dir,
que el valor de x és el doble que el de y. Però continuem sense saber els valors de
x i y.
Per poder resoldre un sistema de N incògnites necessitem tenir N equacions.
En realitat, també necessitem que les equacions siguin linealment independents però, no tindrem en compte
aquesta exigència en aquest nivell introductori.
Anem a resoldre problemes la resolució dels quals requereix el plantejament d'un sistema d'equacions de dimensió 2
(dues equacions i dues incògnites). Si no recordem com resoldre els sistemes (igualació, reducció
i substitució), podem visitar la secció Resolució de sistemes.
Problemes Resolts
Problema 1
Dos nombres sumen 25 i el doble d'un d'ells és 14. Quins nombres són?
Veure Solució
Anomenem x al primer nombre i y al segon.
Com que els nombres sumen 25,
$$ x + y = 25 $$
El doble d'un dels nombres, podem suposar que és x, és 14:
$$ 2x = 14$$
Tenim el sistema d'equacions
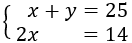
Resolem per substitució
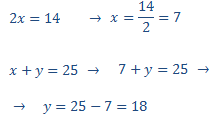
Per tant, els nombres són 7 i 18.
Problema 2
El doble de la suma de dos nombres és 32 i la seva diferència és 0. Quins nombres són?
Veure Solució
Sigui x el primer nombre i y el segon.
El doble de la suma dels nombres és 32:
$$ 2(x + y) = 32$$
La diferència dels nombres és 0:
$$ x - y = 0 $$
Tenim el sistema d'equacions
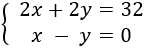
Resolem per reducció:
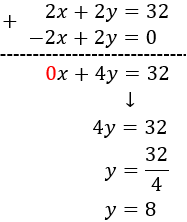
Per tant, els nombres són 8 i 8.
Problema 3
La suma de dos nombres és 12 i la meitat d'un d'ells és el doble de l'altre. Quins nombres són?
Veure Solució
Sigui x el primer nombre i y el segon.
La suma dels nombres és 12:
$$ x + y = 12 $$
La meitat del primer nombre és el doble del segon:
$$ \frac{x}{2} = 2y $$
Tenim el sistema d'equacions:
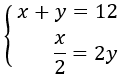
Resolem per substitució:
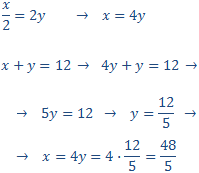
Per tant, els nombres són:
$$ \frac{18}{5}, \ \frac{12}{5} $$
Problema 4
Tenim dos nombres que sumem 0 i si a un d'ells li
sumem 123 obtenim el doble de l'altre. Quins nombres són?
Veure Solució
Anomenem x al primer nombre i y al segon.
La suma dels nombres es 0:
$$ x + y = 0 $$
Si al primer li sumem 123 obtenim el doble del segon:
$$ x + 123 = 2y $$
Tenim el sistema d'equacions:
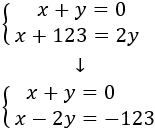
Resolem per substitució:
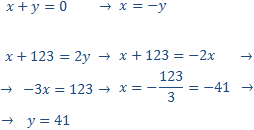
Per tant, els nombres són 41 i -41.
Problema 5
Trobar un nombre de dues xifres que compleix:
- La segona xifra és el doble de la primera
- La suma de les xifres és 12.
Veure Solució
El nombre és xy on x és la primera xifra i y és la segona.
La segona xifra és el doble de la primera:
$$ y = 2x $$
La suma de les xifres és 12:
$$ x + y = 12 $$
Tenim el sistema d'equacions:
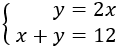
Resolem per substitució
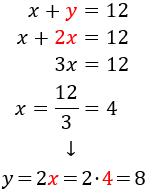
Per tant, el nombre és 48.
Problema 6
Ana té el triple d'edat que el seu fill Jaume. D'ací 15 anys, l'edat d'Ana serà el doble que la del seu fill. Quants anys més que Jaume té sa mare?
Veure Solució
Anomen a a l'edat d'Ana i j a la de Jaume. Escollim aquests noms perquè sigui més
fàcil de reconèixer cada incògnita.
L'edat d'Ana és el triple que la de Jaume:
$$ a = 3j $$
D'ací 15 anys, l'edat d'Ana serà el doble que la de Jaume:
$$ ( a + 15 ) = 2( j + 15 )$$
Notem que quan passen els 15 anys tant Ana com Jaume tindran 15 anys més.
Tenim el sistema d'equacions lineals:
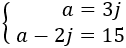
Resolem el sistema per substitució:
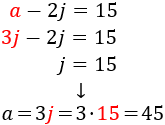
Ana té 45 anys i el seu fill Jaume en té 15. Per tant, Ana
té 30 anys més que el seu fill.
Problema 7
Hem comprat 3 bales de vidre i 2 d'acer per 1,45€ i ahir en vam comprar 2 de vidre i 5 d'acer per 1,7€. Determinar el preu d'una bala de vidre i d'una d'acer.
Veure Solució
Siguen c el nombre de bales de vidre i a el nombre de bales d'acer.
Com que 3 bales de vidre i 2 d'acer costen 4€:
$$ 3c + 2a = 1,45 $$
Com que 2 bales de vidre i 5 d'acer costen 6€:
$$ 2c + 5a = 1,7 $$
Tenim el sistema d'equacions lineals:
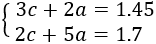
El resolem per reducció:
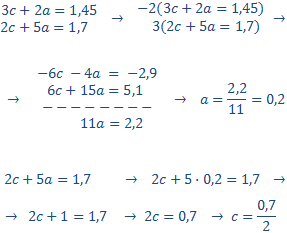
Un bala d'acer costa 0.2€ i una de vidre costa 0.35€.
Problema 8
Trobar la mesura dels costats d'un rectangle que
té perímetre 24 i el costat major és el triple de
gran que el menor.
Veure Solució
Els rectangles consten de quatre costats: dos costats iguals (base) i altres dos costats iguals (altura).
El perímetre és la suma de tots els costats.
Sigui x el costat major i sigui y el costat menor.
El perímetre del rectangle és 24:
$$ 2x + 2y = 24 $$
El costat major és tres vegades més gran que el menor:
$$ x = 3y $$
Tenim el sistema:
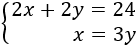
Resolem per substitució:
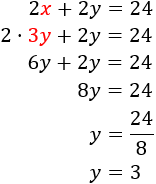
Els costats majors mesuren 9 unitats i els menors 3 unitats (cadascun d'ell).
Problema 9
Trobar el nombre d'animals d'una granja sabent que:
la suma d'ànecs i de vaques és 132 i la de les seves potes
és 402.
es necessiten uns 200kg al dia per alimentar a
les gallines i als galls. Es té un gall per cada 6
gallines i es sap que una gallina menja una mitjana de
500g, el doble que un gall.
es pensa que la sisena part dels conills s'escapen a
la menjadora de les vaques, la qual cosa suposa que hi ha
el triple d'animals en aquesta menjadora.
Veure Solució
a. Hem de tenir en compte que cada ànec té dues potes i cada vaca en té 4.
Sigui p el nombre d'ànecs i v el de vaques.
La suma dels animals és 132:
$$ p + v = 132 $$
La suma de las potes és 402 (dues potes per ànec i quatre per vaca):
$$ 2p + 4v = 402 $$
Tenim el sistema d'equacions
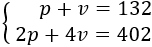
Resolem per reducció
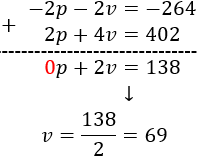
Ha hi 63 ànecs i 69 vaques.
b. Com que les quantitats de pinso que consumeixen són aproximades, no
obtindrem el nombre exacte d'animals, sinó un estimació.
Siguin y el nombre de galls i x el de gallines.
Hi ha un gall per cada 6 gallines:
$$ x = 6y $$
Una gallina menja 0,5kg i un gall 0,25kg. En total consumeixen 200kg:
$$ 0,5x + 0,25y = 200 $$
Tenim el sistema
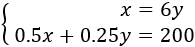
Apliquem substitució:
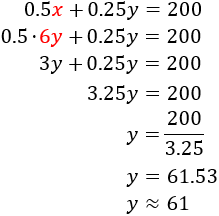
Els resultats són amb decimals ja que les quantitats de menjar que consumeixen són
aproximades.
Podem dir que hi ha 61 galls i 366 gallines.
c. Sabem que hi ha 69 vaques.
Sigui c el nombre de conills.
La sisena part de conills està amb les vaques, pel que hi ha
$$ 69 + \frac{c}{6} $$
animals en la menjadora de les vaques.
Al comptar els conills, el nombre d'animals en la menjadora de les vaques és el triple:
$$ \left( 69 + \frac{c}{6} \right) = 69\cdot 3 $$
Resolem l'equació de primer grau:
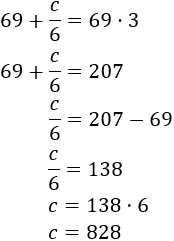
Hi ha 828 conills.
Resumint:
Ànecs: 63
Vaques: 69
Galls: aprox. 61
Gallines: aprox. 366
Conills: 828
Problema 10
En un examen de tipus test, les preguntes correctes
sumen un punt i les incorrectes en resten mig.
En total hi ha 100 preguntes i no s'admeten respostes
en blanc (s'han de contestar totes).
La nota d'un alumne és 8.05 sobre 10. Calcular el nombre
de preguntes que contestà correcta i incorrectament.
Veure Solució
Escrivim la nota sobre 100 en compte de sobre 10:
$$ 8.05 \cdot 10 = 80.5 $$
Anomenem x al nombre de respostes correctes i y al de respostes
incorrectes.
Com que s'han de contestar totes les preguntes, s'ha de complir l'equació següent:
$$ x + y = 100 $$
Cada resposta correcta suma 1 i cada incorrecta en resta 0.5:
$$ 1\cdot x - 0.5 \cdot y = 80.5 $$
Ara resolem el sistema d'equacions per substitució:
Aïllem la x en la primera equació:
$$ x + y = 100 $$
$$ x = 100 - y $$
Ara substituïm x en la segona equació:
$$ x - 0.5 \cdot y = 80.5 $$
$$ (100-y) - 0.5 \cdot y = 80.5 $$
Resolem l'equació de primer grau:
$$ 100-y - 0.5 \cdot y = 80.5 $$
$$ 100-80.5 = y +0.5 y $$
$$ 19.5 = 1.5y$$
$$ y = \frac{19.5}{1.5} = 13$$
Tenim que el nombre de respostes incorrectes és y = 13.
Fàcilment calculem el nombre de respostes correctes:
$$ x = 100 - y = 100 - 13 = 87 $$
Problema 11
Si es suma 7 al numerador i al denominador d'una determinada fracció, s'obté
la fracció
$$ \frac{2}{3} $$
Si en compte de sumar 7 es resta 3 al numerador i al denominador, s'obté la
fracció
$$ \frac{1}{4} $$
Trobar la dita fracció.
Veure Solució
Anomenem x al numerador i y al denominador. És a dir, la fracció és
$$ \frac{x}{y} $$
Sumem 7 al numerador i al denominador i obtenim 2/3:
$$ \frac{x+7}{y+7} = \frac{2}{3} $$
Notem que de la igualtat anterior s'obté la següent:
$$ 3(x+7) = 2(y+7) $$
Operem un poc per simplificar-la:
$$ 3x+21 = 2y+14 $$
$$ 3x -2y = -7 $$
Ara procedim de la mateixa manera però restant 3:
$$ \frac{x-3}{y-3} = \frac{1}{4} $$
Operem un poc:
$$ 4(x-3) = y-3 $$
$$ 4x-12 = y-3 $$
$$ 4x-y = 9 $$
Per tant, el sistema d'equacions lineals és
$$ 3x -2y = -7 $$
$$ 4x-y = 9 $$
Resolem por igualació (per canviar de mètode). Aïllem en ambdues equacions la x.
De la primera equació:
$$ 3x -2y = -7 $$
$$ x = \frac{-7+2y}{3} $$
I de la segona:
$$ 4x-y = 9 $$
$$ x = \frac{9+y}{4} $$
Igualem les x:
$$ \frac{-7+2y}{3} = \frac{9+y}{4}$$
Resolem l'equació de primer grau:
$$ 4(-7+2y) = 3(9+y)$$
$$ -28+8y = 27 + 3y $$
$$ 5y = 55 $$
$$ y = \frac{55}{5} = 11 $$
Calculem x a partir de la y:
$$ x = \frac{-7+2y}{3} =$$
$$ x = \frac{-7+22}{3} =$$
$$ x = \frac{15}{3} =$$
$$ x = 5 $$
Per tant, la fracció buscada és
$$ \frac{x}{y} = \frac{5}{11} $$
Problema 12
Una marca de begudes prepara una llimonada (aigua i concentrat de llima) amb una
quantitat molt precisa dels seus ingredients.
La relació entre les quantitats d'aigua i concentrat de llima és
$$ L_L = \frac{2 L_A}{5} $$
on LL representa els litres de concentrat de llima i
LA els litres d'aigua.
Si es necessiten 20 llimes per obtenir un litre de concentrat de llima, quantes llimes
es necessiten per elaborar 1230 botelles de 2L d'aquesta llimonada?
Veure Solució
Les 1230 botelles de 2L equivalen a un total de
$$ 1230 \cdot 2 = 2460 L $$
de llimonada.
Una de les equacions del sistema és la proporcionada per l'enunciat del problema.
L'altra és la següent:
$$ L_L + L_A = 2460 $$
És a dir, el total de litres de llimonada és la suma dels litres d'aigua i dels litres
de concentrat de llima.
Resolem el sistema per substitució:
De la segona equació:
$$ L_L = 2460 - L_A $$
Substituïm en la primera:
$$ L_L = \frac{2 L_A}{5} $$
$$ 2460 - L_A = \frac{2 L_A}{5} $$
Resolem l'equació de primer grau:
$$ 5\cdot 2460 - 5L_A = 2L_A $$
$$ 12300 = 5L_A + 2L_A $$
$$ 12300 = 7L_A $$
$$ L_A = \frac{12300}{7} = 1757.14L $$
Nota: L indica litres, no té res a veure amb el nombre de les
incògnites.
Ara calculem els litres de concentrat de llima:
$$ L_L = 2460 - 1757.14 = 702.86L $$
Com que es requereixen 20 llimes per a un litre de concentrat i volem
702.86L de concentrat, necessitem
$$ 20\cdot 702.86 = 14057.2 $$
Per tant, es necessiten 14058 llimes.
Problema 13 (dificultat alta):
Amb una corda de 34 metres es pot dibuixar un rectangle (sense que sobre corda) la diagonal del qual mesura 13 metres.
Calcular quant mesuren la base i l'altura del rectangle.
Veure Solució
Siguin b la base del rectangle i a la seva altura.
Notem que la mesura de la corda és el perímetre. Per tant,
$$ 2a + 2b = 34 $$
Si dibuixem la diagonal del rectangle veurem 2 triangles rectangles, sent
la seva hipotenusa la diagonal del rectangle:
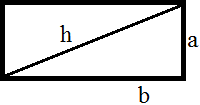
Apliquem el Teorema
de Pitàgores:
$$ a^2 + b^2 = h^2 $$
on h representa la hipotenusa (la diagonal). Llavors
$$ a^2 + b^2 = 13^2 = 169 $$
La dificultat del problema es deu a aquesta última equació ja que no és lineal
(les incògnites estan al quadrat).
Aïllem a en la primera equació:
$$ 2a + 2b = 34 $$
$$ a = \frac{34-2b}{2} = 17-b$$
Y la substituïm en l'equació no lineal:
$$ a^2 + b^2 = 169 $$
$$ (17-b)^2 + b^2 = 169 $$
Calculem el quadrat de la resta (binomi de Newton):
$$ (17-b)^2 = 17^2 +b^2 -2\cdot 17b =$$
$$ = 289 +b^2 -34b $$
Per tant, tenim una equació de segon grau:
$$ 289 +b^2 -34b + b^2 = 169 $$
Simplifiquem un poc:
$$ 2b^2 -34b +120 =0 $$
Ometem el procediment ja que no pertany al tema de sistemes d'equacions.
Les solucions són:
$$ b=12,\ b=5 $$
Pel que a pot tenir dos valors:
$$ a = 17-b = 17-5=12 $$
$$ a = 17-b = 17-12=5 $$
Notem que en realitat només existeix una solució al problema ja que si b = 12 aleshores
a = 5 i si b = 12 aleshores a = 5. Açò es deu a que no importa si considerem
un com la base o com l'altura.
Per tant, els costats del rectangle són de 12 i 5 metres.
Problema 14
En un concert benèfic es venen totes les entrades i es recapten 23 mil dòlars. Els preus de les entrades són 50 dòlars les normals i 300 dòlars les vip.
Calcular el nombre d'entrades venudes de cada tipus si el total d'entrades venudes és de 160.
Veure Solució
Anomenem v al nombre d'entrades vip i n al d'entrades normals
(no importa el nom que li donem a les incògnites).
El nombre total d'entrades és la suma de les entrades vip i les normals:
$$ v + n = 160 $$
La recaptació és
$$ 300v + 50n = 23000 $$
Resolem el sistema d'equacions per igualació. Aïllem v en ambdues
equacions:
De la primera equació:
$$ v = 160-n $$
De la segona equació:
$$ v = \frac{23000 - 50n}{300} $$
Igualem ambdues expressions:
$$ 160-n = \frac{23000 - 50n}{300} $$
La solució de l'equació de primer grau anterior és:
$$ n = 100 $$
Per tant,
$$ v = 160-100 = 60 $$
Per tant, es van vendre 60 entrades vip i 100 normals.
Problema 15
Un nen realitza les següents observacions sobre un parc
infantil de pilotes:
-
Hi ha pilotes verdes, blanques i grogues.
-
El nombre de pilotes verdes i pilotes blanques és cinc vegades el nombre de les grogues.
-
El nombre de pilotes verdes és el triple que el de grogues.
-
El total de pilotes grogues i blanques és 123.
Veure Solució
Anomenem v al nombre de pilotes verdes, b al nombre de pilotes blanques i g
al nombre de pilotes grogues.
El segon punt ens diu que
$$ v+b = 5g $$
El tercer punt ens diu que
$$ v = 3g $$
I el quart ens diu que
$$ g+b = 123 $$
Tenim un sistema de 3 equacions lineals amb 3 incògnites.
Resolem el sistema por substitució:
Substituïm la v de la segona equació en la primera equació:
$$ v+b = 5g $$
$$ 3g+b = 5g $$
Aïllem b:
$$ b = 5g -3g $$
$$ b = 2g $$
Substituïm b en la tercera equació:
$$ g+b = 123 $$
$$ g+2g = 123 $$
$$ 3g = 123 $$
$$ g = 41 $$
Ara utilitzem el valor de g per obtindre les altres incògnites:
$$ b = 2g = 82 $$
$$ v = 3g = 123 $$
Problema 16
Calcular el nombre de nombres positius de 3 xifres (majors que 99) tals que
una de les seves xifres és 0 i les altres dos xifres sumen 7.
Veure Solució
Com que els nombres són de 3 xifres, seran de la forma
$$ xy0 $$
O bé
$$ x0y $$
on x i y representen xifres.
Notem que els nombres 0xy no són en realitat de tres xifres ja que
0xy = xy.
En els dos casos s'ha de complir que
$$ x+y = 7 $$
Per tant, tenim les possibilitats
| x |
y |
x + y |
| 1 |
6 |
7 |
| 2 |
5 |
7 |
| 3 |
4 |
7 |
| 4 |
3 |
7 |
| 5 |
2 |
7 |
| 6 |
1 |
7 |
| 7 |
0 |
7 |
Notem que x no pot ser 0 ja que és la primera xifra en els dos casos.
En la taula es recullen les 7 possibilitats i són vàlides per als dos casos.
Per tant, en un principi hi ha un total de 14 nombres però, tenim que descomptar-ne un
ja que els valors de l'última fila proporcionen el mateix nombre.
La solució és: 13 nombres.

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.