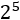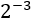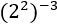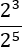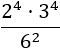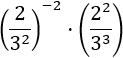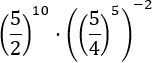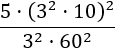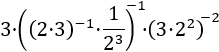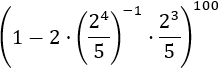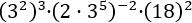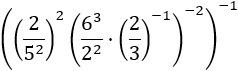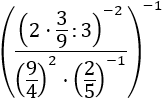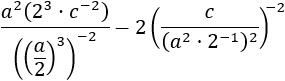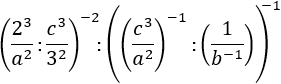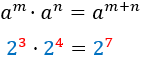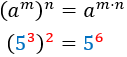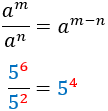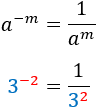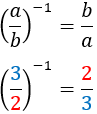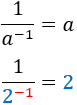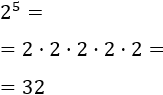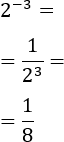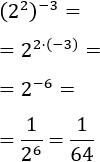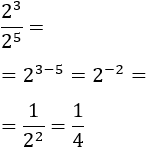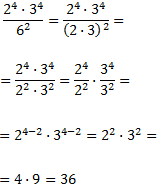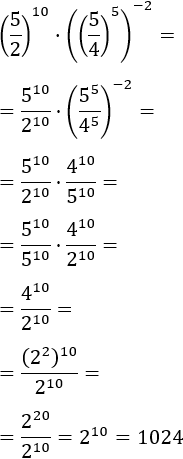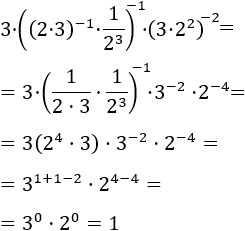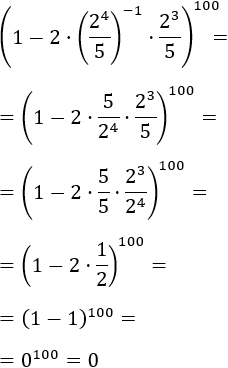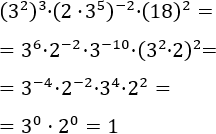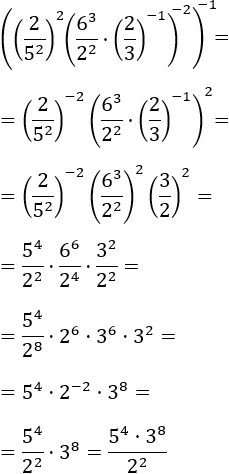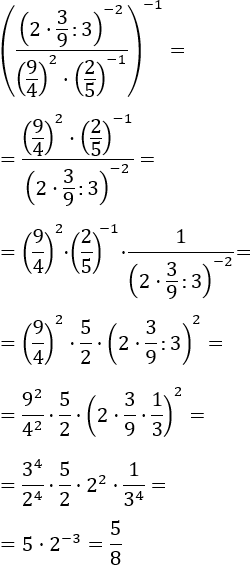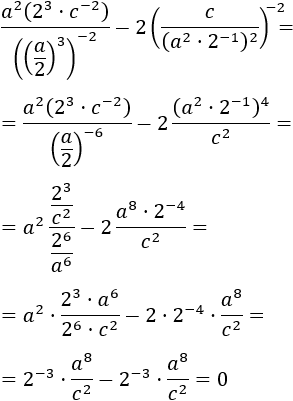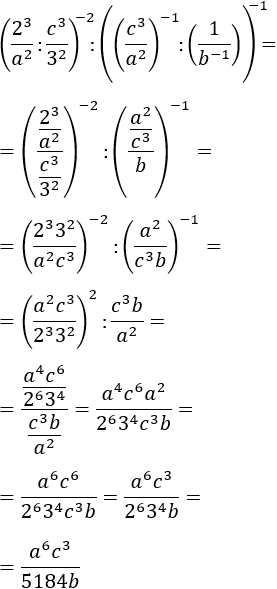Contingut d'aquesta pàgina:
-
Introducció
-
Propietats de les potències
-
15 Exercicis resolts: simplificar potències, des de les més simples a les més complexes (expressions amb parèntesis, signes negatius i paràmetres)
-
No tractarem potències fraccionàries en aquesta secció
Novetat!
Intel·ligència artificial
Com els algorismes condicionen les nostres vides
Enric Senabre, Vicent Costa
Més informació: sembra llibres.
|
 |
Introducció
Una potència és una expressió del tipus
ab = a · a · · · a · a
Aquesta potencia representa el resultat de multiplicar la base, a, per si mateixa tantes vegades com indica l'exponent, b. Ho llegim com "a elevat a b".
Per exemple, 23 = 2·2·2 = 8 (la base és 2 i l'exponent és 3).
En general, tant la base com l'exponent poden ser qualsevol nombre (real o complex) o fins i tot una variable, incògnita o paràmetre. Les equacions en les que la incògnita està als exponents de potències s'anomenen
equacions exponencials.
Un cas especial són les potències amb exponents fraccionaris. En aquest cas, la potència representa una arrel. Sorgeixen per la necessitat de resoldre una equació del tipus x n = a.
Altre cas especial és el de les potències de base 10, és a dir, les de la forma 10 n. Si n és un nombre natural (0, 1, 2, 3, ...) el resultat de la potència és 10...0 sent n el nombre de 0's. Si n és un nombre negatiu (-1, -2, -3, -4,...), el resultat és 0,00...01 on el valor de n
en positiu indica el nombre de 0's, comptant el de davant de la coma. Aquestes potències són les que s'empren en la notació científica.
Finalment, direm que la potència elevat a 0 és sempre igual a 1, és a dir, x0 = 1.
Propietats de les Potències
|
|
Producte
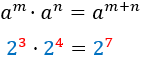
|
Potència
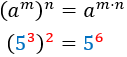
|
| Quocient
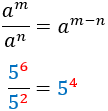
|
Exponent negatiu
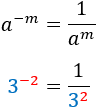
|
| Invers
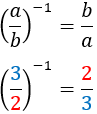
|
Invers
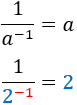
|
15 Exercicis Resolts
(simplificar les expressions)
Exercici 1
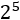
Veure Solució
Apliquem la definició de potència, és a dir, multipliquem la base per si mateixa
tantes vegades com indica l'exponent.
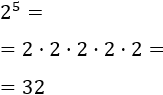
Exercici 2
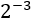
Veure Solució
Com que l'exponent és negatiu, primer expressem la potència com una fracció.
Es queda una potència (amb exponent positiu) en el denominador, així que apliquem la propietat de potència al denominador:
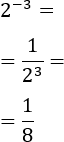
Exercici 3
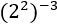
Veure Solució
Tenim la potència d'una potència.
Apliquem la propietat de la potència d'una potència, així que hem de multiplicar ambdós exponents obtenint una potència amb
exponent negatiu. Continuem de la mateixa manera que en l'exercici anterior.
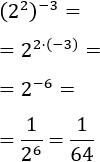
Exercici 4
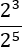
Veure Solució
Tenim el quocient de dues potències. Com que la base és la mateixa,
la propietat diu que es resten els exponents (el del numerador menys el del denominador).
S'obté un exponent negatiu:
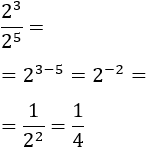
Exercici 5
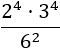
Veure Solució
Tenim un producte de potències en el numerador però no podem calcular-lo al tenir bases distintes (2 i 3).
En el denominador tenim una potència de base 6 que es pot escriure com 3·2.
Escrivim la potència del denominador com
un producte de potències de bases 3 i 2 perquè així tindrem bases en comú i podrem aplicar les propietats:
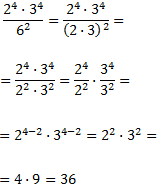
Al escriure la base del denominador com un producte amb les mateixes bases que en el numerador,
podem aplicar les propietats de les potències per simplificar.
Exercici 6
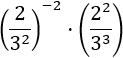
Veure Solució
Primer, podem desfer-nos del signe negatiu de l'exponent de la primera potència
escrivint l'invers de la fracció. D'aquesta manera, tindrem divisions de potències amb les mateixes bases.

Exercici 7
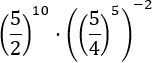
Veure Solució
Apliquem les regles de les potències a cadascuna d'aquestes per simplificar l'expressió.
Transformem les bases en altres per tenir bases comuns.
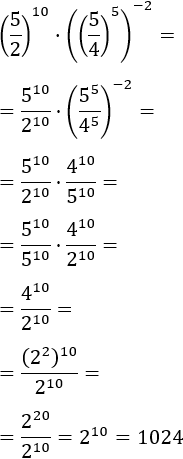
Exercici 8
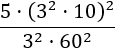
Veure Solució
El major problema en aquesta expressió és el gran nombre de bases distintes que tenen les potències.
El que farem és utilitzar la descomposició de cada base.
Notem que 10 = 2·5 i 60 = 6·10 = 2·3·2·5.
Després, només hem de multiplicar o dividir potències amb base comú:

Exercici 9
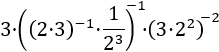
Veure Solució
Apliquem les propietats de les potències: primer per simplificar els parèntesis; després, per calcular l'invers
del producte i multiplicar i dividir les potències.
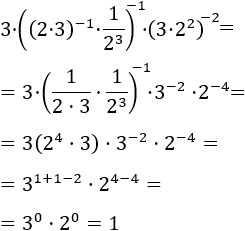
Exercici 10
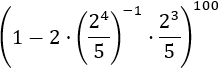
Veure Solució
Tenim un exponent alt però no hem de preocupar-nos per això. L'important
d'aquest exercici és que la base de la potència perquè és tot el parèntesi. El parèntesis és una resta i no tenim regles per desenvolupar la seva potència. Per tant, ens veiem obligats
a treballar a l'interior del parèntesi fins poder aplicar les regles.
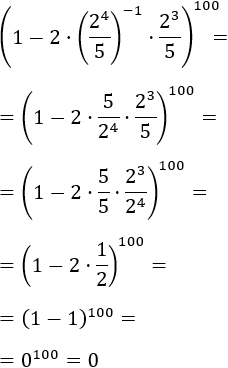
Exercici 11
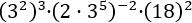
Veure Solució
L'únic problema d'aquest exercici és la potència de base 18 però, podem escriure
18 com 18 = 3·6 = 3·2·3. Després, apliquem les propietats de les potències:
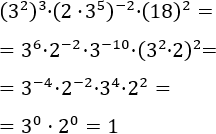
Exercici 12
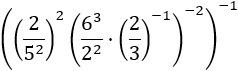
Veure Solució
Tenim molts exponents. Apliquem la propietat al primer, que és la potència d'un producte.
Cal identificar clarament els factors del producte per poder aplicar les regles
sense cometre errors. Després, continuem amb els altres exponents.
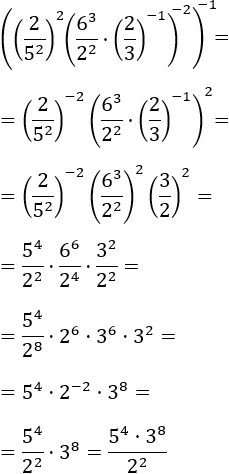
Exercici 13
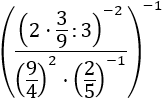
Veure Solució
Ens desfem del primer exponent, que és -1, la qual cosa significa escriure l'invers de
la base. També tenim bases distintes però ja sabem com solucionar-ho: escrivint les bases
com a productes i agrupant les potències. Recordem que el símbol " : " és una divisió,
representa el mateix que " / ".
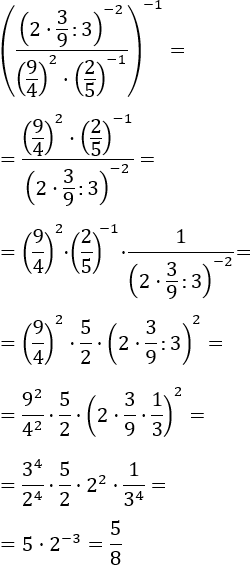
Exercici 14
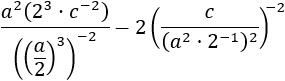
Veure Solució
La característica principal d'aquest exercici són els
paràmetres, és a dir, les lletres. Aquestes lletres solen representar nombres però que,
segons el problema que tractem, poden ser un nombre o un altre. Es treballa
amb els paràmetres de la mateixa manera que amb els nombres.
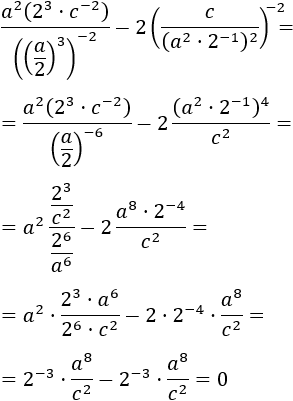
Exercici 15
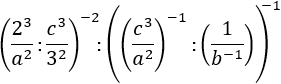
Veure Solució
El més còmode és escriure les divisions ":" en forma de fraccions, "/".
Una vegada fet açò, nomes cal aplicar les propietats.
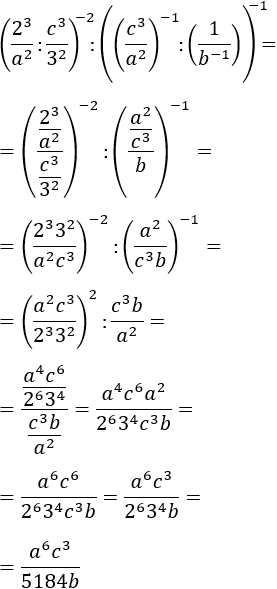

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.